NCERT Exemplar for Class 12 Maths Chapter 10

NCERT Exemplar for Class 12 Maths helps students build strong conceptual knowledge and understanding of the concepts discussed in the chapters. This allows students to increase their thinking, analysing and solving process as well as help boost their confidence significantly. Our subject experts at SimplyAcad have collated all the solutions for the NCERT exemplars to assist students gain valuable insight of the chapter and advanced even more.

Answers of the NCERT exemplar for Class 12 Maths Chapter 10 Vector Algebra contains a total of 18 important questions. Students can easily access them by scrolling below and practise them consistently to score maximum marks. Our subject matter experts at SimplyAcad have put their best to assist students in learning difficult and complex concepts for their effective learning. Along with this, there are several NCERT exemplar for class 12 maths of all the chapters provided on this platform.

Access Solutions of the NCERT Exemplar Class 12 Maths Chapter 4 Vector Algebra

1. Find the unit vector in the direction of the vector \(\mathbf{a}\). \section*

{Solution} The given vector is: \[ \mathbf{a} = \hat{i} + \hat{j} + 2\hat{k} \] The magnitude of vector \(\mathbf{a}\) is given by: \[ |\mathbf{a}| = \sqrt{1^2 + 1^2 + 2^2} = \sqrt{6} \] The unit vector in the direction of \(\mathbf{a}\) is given by: \[ \hat{a} = \frac{\mathbf{a}}{|\mathbf{a}|} = \frac{\hat{i} + \hat{j} + 2\hat{k}}{\sqrt{6}} = \frac{1}{\sqrt{6}} \hat{i} + \frac{1}{\sqrt{6}} \hat{j} + \frac{2}{\sqrt{6}} \hat{k} \] Thus, the unit vector in the direction of \(\mathbf{a}\) is: \[ \boxed{\frac{1}{\sqrt{6}} \hat{i} + \frac{1}{\sqrt{6}} \hat{j} + \frac{2}{\sqrt{6}} \hat{k}} \]

2. If find the unit vector in the direction of

Solution:

3. Find a unit vector in the direction of \(\overrightarrow{PQ}\), where \(P\) and \(Q\) have coordinates \((5, 0, 8)\) and \((3, 3, 2)\), respectively. \section*

{Solution} Given the points \(P(5, 0, 8)\) and \(Q(3, 3, 2)\), The vector \(\overrightarrow{PQ}\) is: \[ \overrightarrow{PQ} = \overrightarrow{OQ} – \overrightarrow{OP} \] where \[ \overrightarrow{OP} = 5\hat{i} + 0\hat{j} + 8\hat{k} \] and \[ \overrightarrow{OQ} = 3\hat{i} + 3\hat{j} + 2\hat{k} \] Thus, \[ \overrightarrow{PQ} = (3\hat{i} + 3\hat{j} + 2\hat{k}) – (5\hat{i} + 0\hat{j} + 8\hat{k}) \] \[ = -2\hat{i} + 3\hat{j} – 6\hat{k} \] To find the unit vector in the direction of \(\overrightarrow{PQ}\), we first need the magnitude of \(\overrightarrow{PQ}\): \[ |\overrightarrow{PQ}| = \sqrt{(-2)^2 + 3^2 + (-6)^2} \] \[ = \sqrt{4 + 9 + 36} \] \[ = \sqrt{49} \] \[ = 7 \] The unit vector in the direction of \(\overrightarrow{PQ}\) is given by: \[ \hat{u} = \frac{\overrightarrow{PQ}}{|\overrightarrow{PQ}|} \] \[ = \frac{-2\hat{i} + 3\hat{j} – 6\hat{k}}{7} \] \[ = -\frac{2}{7}\hat{i} + \frac{3}{7}\hat{j} – \frac{6}{7}\hat{k} \] Hence, the required unit vector in the direction of \(\overrightarrow{PQ}\) is: \[ \boxed{-\frac{2}{7}\hat{i} + \frac{3}{7}\hat{j} – \frac{6}{7}\hat{k}} \]

4. If \(\overrightarrow{a}\) and \(\overrightarrow{b}\) are the position vectors of \(A\) and \(B\), respectively, find the position vector of a point \(C\) in \(\overrightarrow{BA}\) produced such that \(BC = 1.5 \, BA\). \section*

{Solution} Let the position vectors of \(A\) and \(B\) be \(\overrightarrow{a}\) and \(\overrightarrow{b}\), respectively. Then, the vector \(\overrightarrow{BA}\) is given by: \[ \overrightarrow{BA} = \overrightarrow{a} – \overrightarrow{b} \] We are given that \(BC = 1.5 \, BA\). Therefore: \[ \overrightarrow{BC} = 1.5 \, \overrightarrow{BA} \] \[ = 1.5 (\overrightarrow{a} – \overrightarrow{b}) \] To find \(\overrightarrow{OC}\), we use: \[ \overrightarrow{BC} = \overrightarrow{OC} – \overrightarrow{OB} \] \[ \overrightarrow{OC} – \overrightarrow{b} = 1.5 (\overrightarrow{a} – \overrightarrow{b}) \] \[ \overrightarrow{OC} = 1.5 (\overrightarrow{a} – \overrightarrow{b}) + \overrightarrow{b} \] \[ = 1.5 \overrightarrow{a} – 1.5 \overrightarrow{b} + \overrightarrow{b} \] \[ = 1.5 \overrightarrow{a} – 0.5 \overrightarrow{b} \] Thus, the position vector of \(C\) is: \[ \boxed{\overrightarrow{OC} = 1.5 \overrightarrow{a} – 0.5 \overrightarrow{b}} \] Graphically, this represents point \(C\) on the extension of \(\overrightarrow{BA}\) such that the length of \(\overrightarrow{BC}\) is 1.5 times the length of \(\overrightarrow{BA}\).

5. Find the value of \(\lambda\) such that the points \((\lambda, -10, 3)\), \((1, -1, 3)\), and \((3, 5, 3)\) are collinear. \section*

{Solution} Let the points be \( A(\lambda, -10, 3) \), \( B(1, -1, 3) \), and \( C(3, 5, 3) \). The vectors \(\overrightarrow{AB}\) and \(\overrightarrow{AC}\) are given by: \[ \overrightarrow{AB} = (1 – \lambda) \hat{i} + ( -1 + 10) \hat{j} + (3 – 3) \hat{k} = (1 – \lambda) \hat{i} + 9 \hat{j} \] \[ \overrightarrow{AC} = (3 – \lambda) \hat{i} + (5 + 10) \hat{j} + (3 – 3) \hat{k} = (3 – \lambda) \hat{i} + 15 \hat{j} \] For collinearity, \(\overrightarrow{AB}\) must be proportional to \(\overrightarrow{AC}\): \[ \overrightarrow{AB} = k \overrightarrow{AC} \] This gives us: \[ (1 – \lambda) \hat{i} + 9 \hat{j} = k \left[(3 – \lambda) \hat{i} + 15 \hat{j}\right] \] Equating the components, we get two equations: \[ 1 – \lambda = k (3 – \lambda) \] \[ 9 = k \cdot 15 \] From the second equation: \[ k = \frac{9}{15} = \frac{3}{5} \] Substitute \(k\) into the first equation: \[ 1 – \lambda = \frac{3}{5} (3 – \lambda) \] \[ 1 – \lambda = \frac{9 – 3\lambda}{5} \] Multiply through by 5 to clear the fraction: \[ 5 (1 – \lambda) = 9 – 3\lambda \] \[ 5 – 5\lambda = 9 – 3\lambda \] \[ -5\lambda + 3\lambda = 9 – 5 \] \[ -2\lambda = 4 \] \[ \lambda = -2 \] Thus, the value of \(\lambda\) is \(\boxed{-2}\).

6. A vector \(\vec{r}\) is inclined at equal angles to the three axes. If the magnitude of \(\vec{r}\) is \(2\sqrt{3}\) units, find \(\vec{r}\). \section*

{Solution} Given, \[ |\vec{r}| = 2\sqrt{3} \] Since \(\vec{r}\) is equally inclined to the three axes, the direction cosines of the vector \(\vec{r}\) will be equal: \[ l = m = n \] Direction cosines satisfy the equation: \[ l^2 + m^2 + n^2 = 1 \] Substituting \(l = m = n\) into the equation: \[ l^2 + l^2 + l^2 = 1 \] \[ 3l^2 = 1 \] \[ l^2 = \frac{1}{3} \] \[ l = \pm \frac{1}{\sqrt{3}} \] So the vector \(\vec{r}\) can be written as: \[ \vec{r} = |\vec{r}| \left(l \hat{i} + l \hat{j} + l \hat{k}\right) \] \[ \vec{r} = 2\sqrt{3} \left(\frac{1}{\sqrt{3}} \hat{i} + \frac{1}{\sqrt{3}} \hat{j} + \frac{1}{\sqrt{3}} \hat{k}\right) \] \[ \vec{r} = \pm 2 (\hat{i} + \hat{j} + \hat{k}) \] Hence, the required vector is: \[ \vec{r} = \pm 2 (\hat{i} + \hat{j} + \hat{k}) \]

7. A vector \(\vec{r}\) has magnitude 14 and direction ratios \(2, 3, -6\). Find the direction cosines and components of \(\vec{r}\), given that \(\vec{r}\) makes an acute angle with the \(x\)-axis. \section*

{Solution} Let the vector \(\vec{r} = a\hat{i} + b\hat{j} + c\hat{k}\). \[ \text{Given that the direction ratios of } \vec{r} \text{ are } 2, 3, -6 \] Hence, \[ \frac{a}{2} = \frac{b}{3} = \frac{c}{-6} = \lambda \quad \text{(say)} \] \[ \Rightarrow a = 2\lambda, \quad b = 3\lambda, \quad c = -6\lambda \] \[ \text{Thus, } \vec{r} = \lambda(2\hat{i} + 3\hat{j} – 6\hat{k}) \quad \text{(1)} \] Now, the magnitude of \(\vec{r}\) is given by \[ |\vec{r}| = \sqrt{\lambda^2(4 + 9 + 36)} = \sqrt{\lambda^2 \times 49} = 7|\lambda| \] Given that \(|\vec{r}| = 14\), \[ 14 = 7|\lambda| \] \[ \Rightarrow \lambda = \pm 2 \] Since \(\vec{r}\) makes an acute angle with the \(x\)-axis, we take \(\lambda = 2\) (positive value), \[ \Rightarrow \vec{r} = 4\hat{i} + 6\hat{j} – 12\hat{k} \] The unit vector in the direction of \(\vec{r}\) is given by: \[ \hat{r} = \frac{\vec{r}}{|\vec{r}|} = \frac{4\hat{i} + 6\hat{j} – 12\hat{k}}{14} = \frac{2}{7}\hat{i} + \frac{3}{7}\hat{j} – \frac{6}{7}\hat{k} \] If \(l\), \(m\), and \(n\) are the direction cosines of vector \(\vec{r}\), then: \[ \hat{r} = l\hat{i} + m\hat{j} + n\hat{k} \] Hence, the direction cosines of \(\vec{r}\) are \(\frac{2}{7}, \frac{3}{7}, \frac{-6}{7}\). The components of \(\vec{r}\) are \(4\hat{i}\), \(6\hat{j}\), and \(-12\hat{k}\).

8. Find a vector of magnitude 6, which is perpendicular to both the vectors \(2\hat{i} – \hat{j} + 2\hat{k}\) and \(4\hat{i} – \hat{j} + 3\hat{k}\). \section*

{Solution} Let the vectors be: \[ \vec{a} = 2\hat{i} – \hat{j} + 2\hat{k}, \quad \text{and} \quad \vec{b} = 4\hat{i} – \hat{j} + 3\hat{k} \] Any vector perpendicular to both \(\vec{a}\) and \(\vec{b}\) is given by the cross product \(\vec{a} \times \vec{b}\): \[ \vec{a} \times \vec{b} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & 2 \\ 4 & -1 & 3 \\ \end{vmatrix} \] \[ = \hat{i} \left((-1)(3) – (-1)(2)\right) – \hat{j} \left((2)(3) – (2)(4)\right) + \hat{k} \left((2)(-1) – (4)(-1)\right) \] \[ = \hat{i}(-3 + 2) – \hat{j}(6 – 8) + \hat{k}(-2 + 4) \] \[ = -\hat{i} + 2\hat{j} + 2\hat{k} = \vec{r} \quad \text{(say)} \] The magnitude of \(\vec{r}\) is: \[ |\vec{r}| = \sqrt{(-1)^2 + 2^2 + 2^2} = \sqrt{1 + 4 + 4} = \sqrt{9} = 3 \] A vector of magnitude 6 in the direction of \(\vec{r}\) is given by: \[ \text{Required vector} = \frac{\vec{r}}{|\vec{r}|} \times 6 = \frac{-\hat{i} + 2\hat{j} + 2\hat{k}}{3} \times 6 \] \[ = -2\hat{i} + 4\hat{j} + 4\hat{k} \] Hence, the required vector is \(-2\hat{i} + 4\hat{j} + 4\hat{k}\).

9. Find the angle between the vectors

Solution:

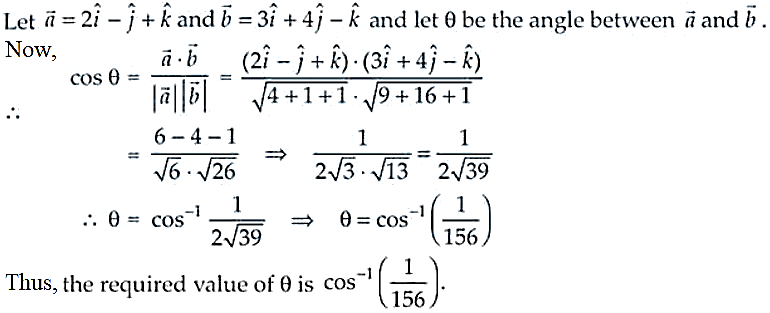
10. If \(\vec{a} + \vec{b} + \vec{c} = 0\), then show that \(\vec{a} \times \vec{b} = \vec{b} \times \vec{c} = \vec{c} \times \vec{a}\). Interpret the result geometrically. \section*

{Solution} Given that \(\vec{a} + \vec{b} + \vec{c} = 0\), we have: \[ \Rightarrow \vec{b} = -\vec{c} – \vec{a} \] Now, \[ \vec{a} \times \vec{b} = \vec{a} \times (-\vec{c} – \vec{a}) \] \[ = \vec{a} \times (-\vec{c}) + \vec{a} \times (-\vec{a}) \] \[ = -\vec{a} \times \vec{c} \quad \Rightarrow \quad \vec{a} \times \vec{b} = \vec{c} \times \vec{a} \quad \dots (i) \] Also, \[ \vec{b} \times \vec{c} = (-\vec{c} – \vec{a}) \times \vec{c} \] \[ = (-\vec{c} \times \vec{c}) + (-\vec{a} \times \vec{c}) \] \[ = -\vec{a} \times \vec{c} \quad \Rightarrow \quad \vec{b} \times \vec{c} = \vec{c} \times \vec{a} \quad \dots (ii) \] From Eqs.\((i)\) and \((ii)\), we have: \[ \vec{a} \times \vec{b} = \vec{b} \times \vec{c} = \vec{c} \times \vec{a} \] \section*{Geometrical Interpretation of the Result} If \(ABCD\) is a parallelogram such that \(\overrightarrow{AB} = \vec{a}\) and \(\overrightarrow{AD} = \vec{b}\), and these adjacent sides are making an angle \(\theta\) between each other, then the area of the parallelogram \(ABCD\) is given by: \[ \text{Area of parallelogram } ABCD = |\vec{a}| |\vec{b}| \sin \theta = |\vec{a} \times \vec{b}| \] Since parallelograms on the same base and between the same parallels are equal in area, we can say that: \[ |\vec{a} \times \vec{b}| = |\vec{a} \times \vec{c}| = |\vec{b} \times \vec{c}| \] This also implies that: \[ \vec{a} \times \vec{b} = \vec{a} \times \vec{c} = \vec{b} \times \vec{c} \] Thus, the areas of the parallelograms formed by taking any two vectors among \(\vec{a}\), \(\vec{b}\), and \(\vec{c}\) as adjacent sides are equal.

11. Find the sine of the angle between the vectors \(\vec{a} = 3\hat{i} + \hat{j} + 2\hat{k}\) and \(\vec{b} = 2\hat{i} – 2\hat{j} + 4\hat{k}\). \section*

{Solution} Given, \(\vec{a} = 3\hat{i} + \hat{j} + 2\hat{k}\) and \(\vec{b} = 2\hat{i} – 2\hat{j} + 4\hat{k}\). The angle \(\theta\) between \(\vec{a}\) and \(\vec{b}\) is given by \[ \cos \theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|} \] Let \(\theta\) be the angle between the vectors \(\vec{a}\) and \(\vec{b}\). \[ \Rightarrow \cos \theta = \frac{(3\hat{i} + \hat{j} + 2\hat{k}) \cdot (2\hat{i} – 2\hat{j} + 4\hat{k})}{\sqrt{3^2 + 1^2 + 2^2} \cdot \sqrt{2^2 + (-2)^2 + 4^2}} \] \[ = \frac{(6 – 2 + 8)}{\sqrt{9 + 1 + 4} \cdot \sqrt{4 + 4 + 16}} \] \[ = \frac{12}{\sqrt{14} \cdot \sqrt{24}} \] \[ = \frac{12}{4\sqrt{21}} \Rightarrow \cos \theta = \frac{3}{\sqrt{21}} \] \[ \Rightarrow \sin \theta = \sqrt{1 – \cos^2 \theta} \quad [\text{since } \sin^2 \theta + \cos^2 \theta = 1] \] \[ = \sqrt{1 – \frac{9}{21}} = \sqrt{\frac{12}{21}} = \frac{2\sqrt{7}}{7} \] Hence, the sine of the angle between the vectors is \(\frac{2\sqrt{7}}{7}\).

12. If \( A \), \( B \), \( C \), \( D \) are the points with position vectors \( \hat{i} + \hat{j} – \hat{k} \), \( 2\hat{i} – \hat{j} + 3\hat{k} \), \( 2\hat{i} – 3\hat{k} \), \( 3\hat{i} – 2\hat{j} + \hat{k} \) respectively, find the projection of \(\overrightarrow{AB}\) along \(\overrightarrow{CD}\). \section*

{Solution} Given, the position vectors of \( A \), \( B \), \( C \), and \( D \) are: \[ \overrightarrow{OA} = \hat{i} + \hat{j} – \hat{k} \quad \text{(1)} \] \[ \overrightarrow{OB} = 2\hat{i} – \hat{j} + 3\hat{k} \quad \text{(2)} \] \[ \overrightarrow{OC} = 2\hat{i} – 3\hat{k} \quad \text{(3)} \] \[ \overrightarrow{OD} = 3\hat{i} – 2\hat{j} + \hat{k} \quad \text{(4)} \] [Where \( O \) is the origin] Now, \[ \overrightarrow{AB} = \overrightarrow{OB} – \overrightarrow{OA} = (2\hat{i} – \hat{j} + 3\hat{k}) – (\hat{i} + \hat{j} – \hat{k}) \] [From equations (1) and (2)] \[ = \hat{i} – 2\hat{j} + 4\hat{k} \quad \text{(5)} \] And \[ \overrightarrow{CD} = \overrightarrow{OD} – \overrightarrow{OC} = (3\hat{i} – 2\hat{j} + \hat{k}) – (2\hat{i} – 3\hat{k}) \] [From equations (3) and (4)] \[ = \hat{i} – 2\hat{j} + 4\hat{k} \quad \text{(6)} \] Therefore, the projection of \(\vec{a}\) along \(\vec{b}\) is given by: \[ \text{Projection of } \vec{a} \text{ along } \vec{b} = \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|} \] So, the projection of \(\overrightarrow{AB}\) along \(\overrightarrow{CD}\) is: \[ \frac{\overrightarrow{AB} \cdot \overrightarrow{CD}}{|\overrightarrow{CD}|} = \frac{(\hat{i} – 2\hat{j} + 4\hat{k}) \cdot (\hat{i} – 2\hat{j} + 4\hat{k})}{\sqrt{1^2 + (-2)^2 + 4^2}} \] [From equations (5) and (6)] \[ = \frac{21}{\sqrt{21}} = \sqrt{21} \text{ units} \] Hence, the projection of \(\overrightarrow{AB}\) along \(\overrightarrow{CD}\) is \(\sqrt{21}\) units.

13. Using vectors, find the area of the triangle ABC with vertices \( A(1, 2, 3) \), \( B(2, -1, 4) \), and \( C(4, 5, -1) \). \section*

{Solution} We first form the vectors \(\overrightarrow{AB}\) and \(\overrightarrow{AC}\): \[ \overrightarrow{AB} = (2-1, -1-2, 4-3) = (1, -3, 1) \] \[ \overrightarrow{AC} = (4-1, 5-2, -1-3) = (3, 3, -4) \] Next, we find their cross product \(\overrightarrow{AB} \times \overrightarrow{AC}\): \[ \overrightarrow{AB} \times \overrightarrow{AC} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & -3 & 1 \\ 3 & 3 & -4 \\ \end{vmatrix} \] \[ = \hat{i}((-3)(-4) – (1)(3)) – \hat{j}((1)(-4) – (1)(3)) + \hat{k}((1)(3) – (-3)(3)) \] \[ = \hat{i}(12 – 3) – \hat{j}(-4 – 3) + \hat{k}(3 + 9) \] \[ = 9\hat{i} + 7\hat{j} + 12\hat{k} \] Now, the magnitude of this cross product is: \[ |\overrightarrow{AB} \times \overrightarrow{AC}| = \sqrt{9^2 + 7^2 + 12^2} = \sqrt{81 + 49 + 144} = \sqrt{274} \approx 16.55 \] The area of the triangle is half the magnitude of the cross product of \(\overrightarrow{AB}\) and \(\overrightarrow{AC}\): \[ \text{Area of triangle} = \frac{1}{2} \times 16.55 = 8.275 \text{ square units} \]

14. Using vectors, prove that parallelograms on the same base and between the same parallels are equal in area. \section*

{Solution} Let \(ABCD\) and \(ABC’D’\) be two parallelograms on the same base \(AB\) and between the same parallels \(l\) and \(m\). The vector area of parallelogram \(ABCD\) is given by: \[ \text{Area of } ABCD = \overrightarrow{AB} \times \overrightarrow{AD} \] Now consider the area of parallelogram \(ABC’D’\): \[ \text{Area of } ABC’D’ = \overrightarrow{AB} \times \overrightarrow{AD’} \] Since \(DD’\) is parallel to \(AB\), we can write: \[ \overrightarrow{AD} = \overrightarrow{AD’} + \overrightarrow{D’D} \] Thus, the vector area of parallelogram \(ABCD\) can be expressed as: \[ \overrightarrow{AB} \times \overrightarrow{AD} = \overrightarrow{AB} \times (\overrightarrow{AD’} + \overrightarrow{D’D}) \] Expanding this: \[ \overrightarrow{AB} \times \overrightarrow{AD} = \overrightarrow{AB} \times \overrightarrow{AD’} + \overrightarrow{AB} \times \overrightarrow{D’D} \] Since \(\overrightarrow{AB}\) and \(\overrightarrow{D’D}\) are parallel, their cross product is zero: \[ \overrightarrow{AB} \times \overrightarrow{D’D} = 0 \] Therefore, the area of parallelogram \(ABCD\) becomes: \[ \overrightarrow{AB} \times \overrightarrow{AD} = \overrightarrow{AB} \times \overrightarrow{AD’} \] This shows that the vector area of parallelogram \(ABCD\) is equal to the vector area of parallelogram \(ABC’D’\). Hence, parallelograms on the same base and between the same parallels are equal in area. \(\blacksquare\)

Long Answer (L.A.)

15. Prove that in any \( \triangle ABC \), \[ \cos A = \frac{b^2 + c^2 – a^2}{2bc}, \] where \(a\), \(b\), and \(c\) are the magnitudes of the sides opposite to the vertices \(A\), \(B\), and \(C\), respectively. \section*

{Solution} Let’s consider triangle \( \triangle ABC \). In \( \triangle ABC \): – \(a\) is the side opposite to vertex \(A\), – \(b\) is the side opposite to vertex \(B\), – \(c\) is the side opposite to vertex \(C\). To prove the cosine rule, we use the following steps. Let us drop a perpendicular from \(C\) onto \(AB\), meeting \(AB\) at point \(D\). Then the components of \(c\) along \(AB\) are \(c \cos A\) and \(c \sin A\). Since, \[ CD = b – c \cos A \] In \( \triangle BDC \), by applying the Pythagorean theorem, we have: \[ a^2 = (b – c \cos A)^2 + (c \sin A)^2 \] Expanding and simplifying: \[ a^2 = b^2 – 2bc \cos A + c^2 \cos^2 A + c^2 \sin^2 A \] Since \( \cos^2 A + \sin^2 A = 1 \), we have: \[ a^2 = b^2 + c^2 – 2bc \cos A \] Rearranging the terms to solve for \( \cos A \), we get: \[ 2bc \cos A = b^2 + c^2 – a^2 \] \[ \therefore \cos A = \frac{b^2 + c^2 – a^2}{2bc} \] Hence, the proof is complete. \( \blacksquare \)

16. If \( \vec{a}, \vec{b}, \) and \( \vec{c} \) determine the vertices of a triangle, show that \[ \frac{1}{2} \left[ \vec{b} \times \vec{c} + \vec{c} \times \vec{a} + \vec{a} \times \vec{b} \right] \] gives the vector area of the triangle. Hence, deduce the condition that the three points \( \vec{a}, \vec{b}, \) and \( \vec{c} \) are collinear. Also, find the vector normal to the plane of the triangle. \section*

{Solution} Given that \( \vec{a}, \vec{b}, \) and \( \vec{c} \) are the vertices of a \( \triangle ABC \), as shown in the figure. The area of \( \triangle ABC \) is given by: \[ \text{Area of } \triangle ABC = \frac{1}{2} \left| \vec{AB} \times \vec{AC} \right| \] Now, we can express \( \vec{AB} \) and \( \vec{AC} \) as: \[ \vec{AB} = \vec{b} – \vec{a} \quad \text{and} \quad \vec{AC} = \vec{c} – \vec{a} \] So, the area of \( \triangle ABC \) becomes: \[ \text{Area of } \triangle ABC = \frac{1}{2} \left| (\vec{b} – \vec{a}) \times (\vec{c} – \vec{a}) \right| \] Expanding the cross product: \[ \vec{AB} \times \vec{AC} = (\vec{b} – \vec{a}) \times (\vec{c} – \vec{a}) = \vec{b} \times \vec{c} – \vec{b} \times \vec{a} – \vec{a} \times \vec{c} + \vec{a} \times \vec{a} \] Since \( \vec{a} \times \vec{a} = \vec{0} \) (cross product of any vector with itself is zero), we have: \[ \vec{AB} \times \vec{AC} = \vec{b} \times \vec{c} – \vec{b} \times \vec{a} – \vec{a} \times \vec{c} \] This simplifies to: \[ \vec{AB} \times \vec{AC} = \vec{b} \times \vec{c} + \vec{a} \times \vec{b} + \vec{c} \times \vec{a} \] Therefore, the area of \( \triangle ABC \) can be written as: \[ \text{Area of } \triangle ABC = \frac{1}{2} \left| \vec{b} \times \vec{c} + \vec{a} \times \vec{b} + \vec{c} \times \vec{a} \right| \] \[ \text{Hence, the vector area of the triangle is } \frac{1}{2} \left[ \vec{b} \times \vec{c} + \vec{c} \times \vec{a} + \vec{a} \times \vec{b} \right]. \] \subsection*{Condition for Collinearity} For the three points \( \vec{a}, \vec{b}, \) and \( \vec{c} \) to be collinear, the area of the triangle must be zero. \[ \frac{1}{2} \left[ \vec{b} \times \vec{c} + \vec{c} \times \vec{a} + \vec{a} \times \vec{b} \right] = 0 \] This implies: \[ \vec{b} \times \vec{c} + \vec{c} \times \vec{a} + \vec{a} \times \vec{b} = 0 \] This is the required condition for the collinearity of three points \( \vec{a}, \vec{b}, \) and \( \vec{c} \). \subsection*{Vector Normal to the Plane} Let \( \hat{n} \) be the unit vector normal to the plane of \( \triangle ABC \). The normal vector \( \vec{n} \) is given by the cross product: \[ \vec{n} = \vec{AB} \times \vec{AC} = \vec{b} \times \vec{c} + \vec{c} \times \vec{a} + \vec{a} \times \vec{b} \] The unit normal vector is: \[ \hat{n} = \frac{\vec{n}}{\left| \vec{n} \right|} = \frac{\vec{b} \times \vec{c} + \vec{c} \times \vec{a} + \vec{a} \times \vec{b}}{\left| \vec{b} \times \vec{c} + \vec{c} \times \vec{a} + \vec{a} \times \vec{b} \right|} \] This \( \hat{n} \) is the required unit vector normal to the plane of the triangle.

17. Show that the area of the parallelogram whose diagonals are given by \( \vec{a} \) and \( \vec{b} \) is \( \frac{1}{2} |\vec{a} \times \vec{b}| \). Also, find the area of the parallelogram whose diagonals are \( 2\hat{i} – \hat{j} + \hat{k} \) and \( \hat{i} + 3\hat{j} – \hat{k} \). \section*

{Solution} Let \( ABCD \) be a parallelogram such that: \[ \vec{AB} = \vec{p}, \quad \vec{AD} = \vec{q} \] \[ \Rightarrow \vec{BC} = \vec{q} \] By the triangle law of addition, we get: \[ \vec{AC} = \vec{p} + \vec{q} = \vec{a} \quad \text{(say)} \quad \dots (i) \] Similarly: \[ \vec{BD} = -\vec{p} + \vec{q} = \vec{b} \quad \text{(say)} \quad \dots (ii) \] On adding equations (i) and (ii), we get: \[ \vec{a} + \vec{b} = 2\vec{q} \quad \Rightarrow \quad \vec{q} = \frac{1}{2} (\vec{a} + \vec{b}) \] On subtracting equation (ii) from equation (i), we get: \[ \vec{a} – \vec{b} = 2\vec{p} \quad \Rightarrow \quad \vec{p} = \frac{1}{2} (\vec{a} – \vec{b}) \] Now, \[ \vec{p} \times \vec{q} = \frac{1}{4} (\vec{a} – \vec{b}) \times (\vec{a} + \vec{b}) \] Expanding the cross product: \[ \vec{p} \times \vec{q} = \frac{1}{4} \left[ \vec{a} \times \vec{a} + \vec{a} \times \vec{b} – \vec{b} \times \vec{a} – \vec{b} \times \vec{b} \right] \] Since \( \vec{a} \times \vec{a} = \vec{0} \) and \( \vec{b} \times \vec{b} = \vec{0} \), we get: \[ \vec{p} \times \vec{q} = \frac{1}{4} \left[ \vec{a} \times \vec{b} + \vec{a} \times \vec{b} \right] = \frac{1}{2} (\vec{a} \times \vec{b}) \] So, the area of the parallelogram \( ABCD \) is: \[ \text{Area} = \left| \vec{p} \times \vec{q} \right| = \frac{1}{2} \left| \vec{a} \times \vec{b} \right| \] Now, to find the area of the parallelogram whose diagonals are \( 2\hat{i} – \hat{j} + \hat{k} \) and \( \hat{i} + 3\hat{j} – \hat{k} \): \[ \text{Area} = \frac{1}{2} \left| \left(2\hat{i} – \hat{j} + \hat{k}\right) \times \left(\hat{i} + 3\hat{j} – \hat{k}\right) \right| \] The cross product is: \[ \left(2\hat{i} – \hat{j} + \hat{k}\right) \times \left(\hat{i} + 3\hat{j} – \hat{k}\right) = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & -1 & 1 \\ 1 & 3 & -1 \\ \end{vmatrix} \] This determinant expands to: \[ \hat{i} \left((-1) \times (-1) – (3) \times (1)\right) – \hat{j} \left((2) \times (-1) – (1) \times (1)\right) + \hat{k} \left((2) \times (3) – (-1) \times (1)\right) \] \[ = \hat{i} \left(1 – 3\right) – \hat{j} \left(-2 – 1\right) + \hat{k} \left(6 + 1\right) \] \[ = -2\hat{i} + 3\hat{j} + 7\hat{k} \] So, the magnitude is: \[ \frac{1}{2} \left| -2\hat{i} + 3\hat{j} + 7\hat{k} \right| = \frac{1}{2} \sqrt{(-2)^2 + 3^2 + 7^2} = \frac{1}{2} \sqrt{4 + 9 + 49} = \frac{1}{2} \sqrt{62} \] Thus, the area of the parallelogram is: \[ \frac{1}{2} \sqrt{62} \text{ square units} \]

18. If find a vector such that

Solution:

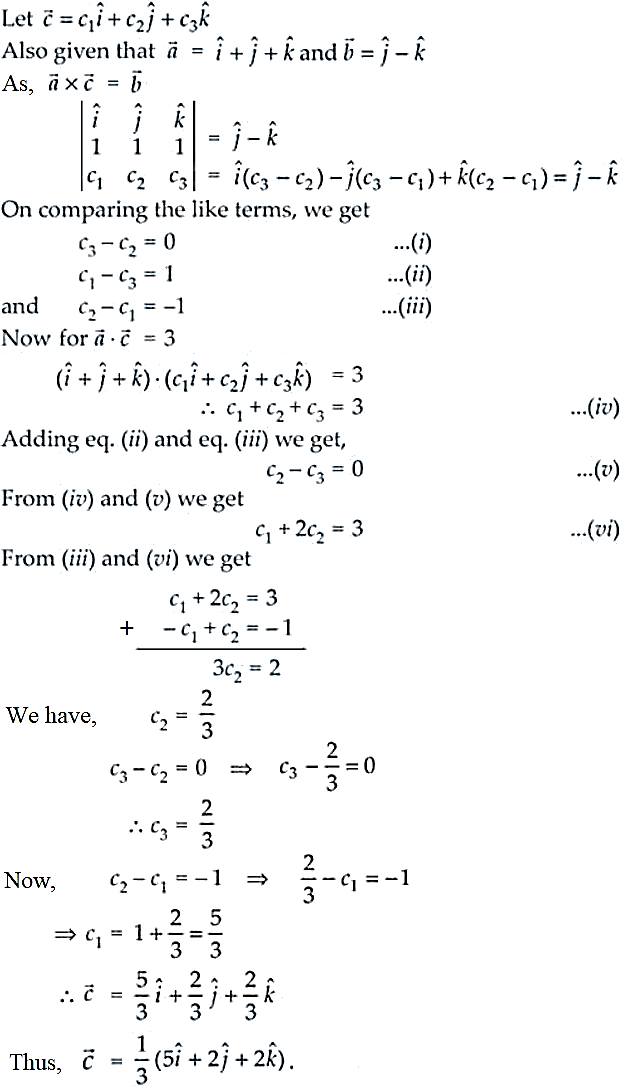
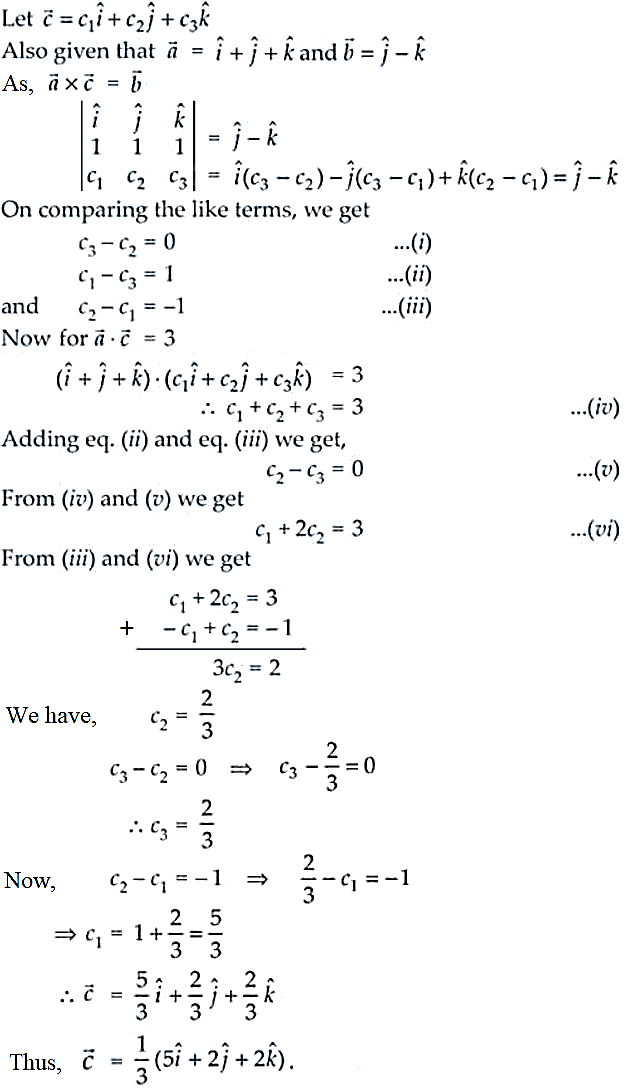
NCERT Exemplar For Class 12 Maths

The NCERT exemplars are an effective study material for scoring higher marks in the examination paper. Students must practise these additional questions for their own benefits, as these are curated by the best subject-matter experts to boost both knowledge and confidence. Students can easily access the ncert exemplar for class 12 maths by visiting our website SimplyAcad and solve all the questions listed to secure maximum marks.

Here are some other NCERT exemplar for class 12 maths:

NCERT exemplar for class 12 maths Chapter 1	NCERT exemplar for class 12 maths Chapter 7
NCERT exemplar for class 12 maths Chapter 2	NCERT exemplar for class 12 maths Chapter 8
NCERT exemplar for class 12 maths Chapter 3	NCERT exemplar for class 12 maths Chapter 9
NCERT exemplar for class 12 maths Chapter 5	NCERT exemplar for class 12 maths Chapter 11
NCERT exemplar for class 12 maths Chapter 6	NCERT exemplar for class 12 maths Chapter 12