NCERT Exemplar Class 12 Maths Chapter 11 Three Dimensional Geometry
NCERT Exemplar for Class 12 Maths Chapter 11
Students willing to get a better understanding of the mathematical chapters must refer to the NCERT Exemplar for Class 12 Maths to grasp the in-depth knowledge of the chapters. The given solutions set helps in providing the students with conceptual knowledge and boost their confidence. Students will be able to solve as many possible questions through the exemplars for regular practices and revisions. The step wise solutions allow them to observe, analyse and learn each step of the answer which is a must for students preparing for their upcoming 12th board examinations. NCERT exemplar for Class 12 Maths Chapter 11 Three Dimensional Geometry contains a total of 24 questions of short and long type.
Students can easily access them by scrolling below and practise them consistently to score maximum marks. Our subject matter experts at SimplyAcad have put their best to assist students in learning difficult and complex concepts for their effective learning. Along with this, there are several NCERT exemplar for class 12 maths of all the chapters provided on this platform.
Access Solutions of the NCERT Exemplar Class 12 Maths Chapter 11 Three Dimensional Geometry – Short Answer (S.A.)
1. Find the position vector of a point \( A \) in space such that \( \overrightarrow{OA} \) is inclined at \( 60^\circ \) to \( OX \) and at \( 45^\circ \) to \( OY \) and \( |\overrightarrow{OA}| = 10 \) units. \section*
{Solution} Let \( \overrightarrow{OA} = \vec{r} = x \hat{i} + y \hat{j} + z \hat{k} \). Since \( \overrightarrow{OA} \) is inclined at \( 60^\circ \) to \( OX \), the direction cosines with \( \hat{i} \) is \( \cos 60^\circ \). Hence: \[ \cos 60^\circ = \frac{x}{|\overrightarrow{OA}|} = \frac{1}{2} \] Thus, \[ x = \frac{1}{2} |\overrightarrow{OA}| \] Similarly, since \( \overrightarrow{OA} \) is inclined at \( 45^\circ \) to \( OY \), the direction cosines with \( \hat{j} \) is \( \cos 45^\circ \). Hence: \[ \cos 45^\circ = \frac{y}{|\overrightarrow{OA}|} = \frac{1}{\sqrt{2}} \] Thus, \[ y = \frac{1}{\sqrt{2}} |\overrightarrow{OA}| \] Let \( \alpha \) be the angle that \( \overrightarrow{OA} \) makes with \( OZ \). Therefore, \[ \cos \alpha = \frac{z}{|\overrightarrow{OA}|} \] From the direction cosines, we have: \[ \cos^2 60^\circ + \cos^2 45^\circ + \cos^2 \alpha = 1 \] Substituting the known values: \[ \left(\frac{1}{2}\right)^2 + \left(\frac{1}{\sqrt{2}}\right)^2 + \cos^2 \alpha = 1 \] \[ \frac{1}{4} + \frac{1}{2} + \cos^2 \alpha = 1 \] \[ \frac{1}{4} + \frac{1}{2} = \frac{3}{4} \] \[ \cos^2 \alpha = 1 – \frac{3}{4} = \frac{1}{4} \] \[ \cos \alpha = \frac{1}{2} \implies \alpha = 60^\circ \] Thus: \[ z = \frac{1}{2} |\overrightarrow{OA}| \] Given \( |\overrightarrow{OA}| = 10 \), we find: \[ x = \frac{1}{2} \times 10 = 5 \] \[ y = \frac{1}{\sqrt{2}} \times 10 = 5 \sqrt{2} \] \[ z = \frac{1}{2} \times 10 = 5 \] Therefore, the position vector of the point \( A \) is: \[ \overrightarrow{OA} = 5 \hat{i} + 5 \sqrt{2} \hat{j} + 5 \hat{k} \]
2. Find the vector equation of the line which is parallel to the vector \(3 \hat{i} – 2 \hat{j} + 6 \hat{k}\) and which passes through the point \((1, -2, 3)\). \section*
{Solution} The vector equation of a line passing through a point \( P (\vec{a}) \) and parallel to a given vector \( \vec{b} \) is given by: \[ \vec{r} = \vec{a} + \lambda \vec{b} \] Here, the line is parallel to \( 3 \hat{i} – 2 \hat{j} + 6 \hat{k} \) and passes through the point \((1, -2, 3)\). Therefore, the vector equation of the line is: \[ \vec{r} = \hat{i} – 2 \hat{j} + 3 \hat{k} + \lambda (3 \hat{i} – 2 \hat{j} + 6 \hat{k}) \] Substituting \(\vec{r} = x \hat{i} + y \hat{j} + z \hat{k}\), we get: \[ x \hat{i} + y \hat{j} + z \hat{k} = \hat{i} – 2 \hat{j} + 3 \hat{k} + \lambda (3 \hat{i} – 2 \hat{j} + 6 \hat{k}) \] Equating the coefficients of \( \hat{i} \), \( \hat{j} \), and \( \hat{k} \), we obtain: \[ (x – 1) \hat{i} + (y + 2) \hat{j} + (z – 3) \hat{k} = \lambda (3 \hat{i} – 2 \hat{j} + 6 \hat{k}) \] Thus, the vector equation of the required line is: \[ (x – 1) \hat{i} + (y + 2) \hat{j} + (z – 3) \hat{k} = \lambda (3 \hat{i} – 2 \hat{j} + 6 \hat{k}) \]
3. Show that the lines
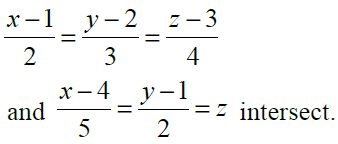
Also, find their point of intersection.
Solution:
Given equation are,
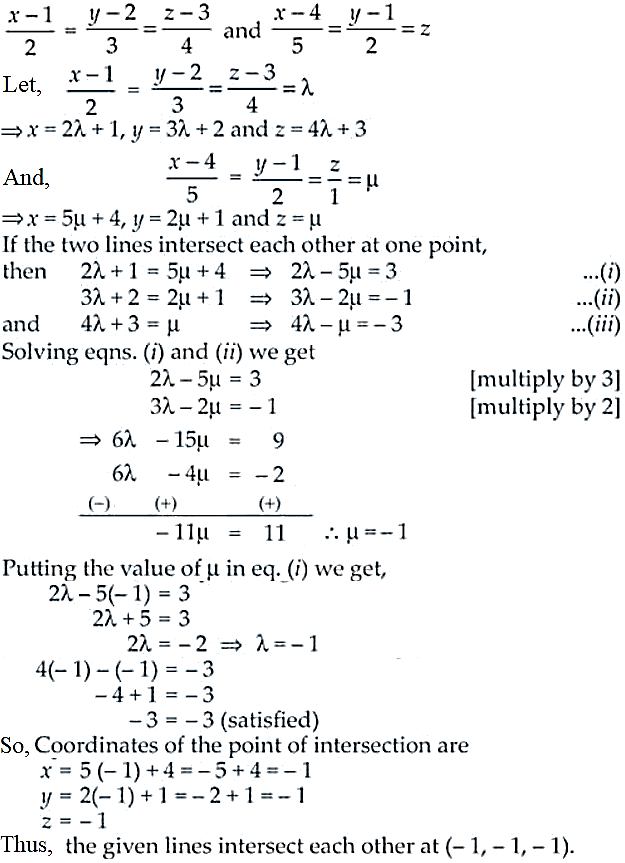
4. Find the angle between the lines
![]()
Solution:
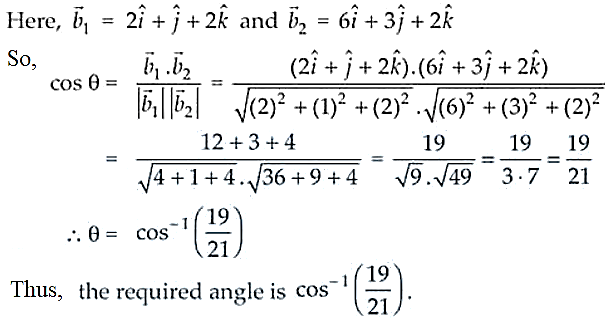
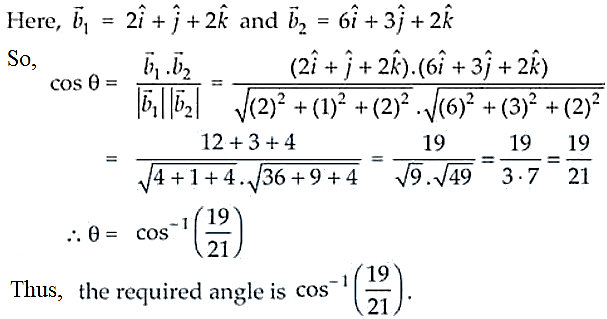
5. Prove that the line through A (0, –1, –1) and B (4, 5, 1) intersects the line through C (3, 9, 4) and D (– 4, 4, 4).
Solution:
Given points, A (0, –1, –1) and B (4, 5, 1)
C (3, 9, 4) and D (– 4, 4, 4).
Cartesian form of equation AB is

6. Prove that the lines \[ x = py + q, \quad z = ry + s \] and \[ x = p’y + q’, \quad z = r’y + s’ \] are perpendicular if \[ pp’ + rr’ + 1 = 0. \] \section*
{Solution} \textbf{1. Representing the Lines in Vector Form} For the line \(L_1\): \[ x = py + q \] \[ z = ry + s \] Rewriting \(L_1\) in vector form, with \(y = t\), we get: \[ \vec{r}_1 = (pt + q) \hat{i} + t \hat{j} + (rt + s) \hat{k} \] The direction vector \(\vec{a}\) of \(L_1\) is: \[ \vec{a} = p \hat{i} + \hat{j} + r \hat{k} \] For the line \(L_2\): \[ x = p’y + q’ \] \[ z = r’y + s’ \] Similarly, with \(y = t\), we get: \[ \vec{r}_2 = (p’t + q’) \hat{i} + t \hat{j} + (r’t + s’) \hat{k} \] The direction vector \(\vec{b}\) of \(L_2\) is: \[ \vec{b} = p’ \hat{i} + \hat{j} + r’ \hat{k} \] \textbf{2. Checking Perpendicularity} The lines \(L_1\) and \(L_2\) are perpendicular if their direction vectors \(\vec{a}\) and \(\vec{b}\) are perpendicular. We compute the dot product \(\vec{a} \cdot \vec{b}\): \[ \vec{a} \cdot \vec{b} = (p \hat{i} + \hat{j} + r \hat{k}) \cdot (p’ \hat{i} + \hat{j} + r’ \hat{k}) \] \[ \vec{a} \cdot \vec{b} = p \cdot p’ + 1 \cdot 1 + r \cdot r’ \] \[ \vec{a} \cdot \vec{b} = pp’ + 1 + rr’ \] The lines are perpendicular if: \[ \vec{a} \cdot \vec{b} = 0 \] Thus, \[ pp’ + 1 + rr’ = 0 \] or equivalently, \[ pp’ + rr’ + 1 = 0 \] \textbf{3. Conclusion} Therefore, the lines \(L_1\) and \(L_2\) are perpendicular if the condition \(pp’ + rr’ + 1 = 0\) is satisfied.
7. Find the equation of a plane which bisects perpendicularly the line joining the points \( A(2, 3, 4) \) and \( B(4, 5, 8) \) at right angles. \section*
{Solution} \textbf{1. Find the Midpoint of \( A \) and \( B \)} The midpoint \( C \) of the line segment \( AB \) is given by: \[ C = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2} \right) \] Substituting \( A(2, 3, 4) \) and \( B(4, 5, 8) \): \[ C = \left( \frac{2 + 4}{2}, \frac{3 + 5}{2}, \frac{4 + 8}{2} \right) = (3, 4, 6) \] \textbf{2. Find the Direction Vector of \( AB \)} The direction vector \( \vec{AB} \) is: \[ \vec{AB} = \langle 4 – 2, 5 – 3, 8 – 4 \rangle = \langle 2, 2, 4 \rangle \] \textbf{3. Normalize the Direction Vector} To get the normal vector of the plane that bisects \( AB \) perpendicularly, use the direction vector \( \vec{AB} \). The direction vector \( \langle 2, 2, 4 \rangle \) can be simplified to \( \langle 1, 1, 2 \rangle \). Therefore, the normal vector to the plane is: \[ \vec{n} = \langle 1, 1, 2 \rangle \] \textbf{4. Find the Equation of the Plane} The general equation of a plane is given by: \[ \vec{r} \cdot \vec{n} = d \] where \( \vec{n} \) is the normal vector and \( \vec{r} = \langle x, y, z \rangle \). Substituting the normal vector \( \langle 1, 1, 2 \rangle \) and the point \( C(3, 4, 6) \) into the plane equation: \[ \langle x, y, z \rangle \cdot \langle 1, 1, 2 \rangle = d \] Substitute \( C(3, 4, 6) \): \[ 3 \cdot 1 + 4 \cdot 1 + 6 \cdot 2 = d \] \[ 3 + 4 + 12 = d \] \[ d = 19 \] Therefore, the plane equation is: \[ x + y + 2z = 19 \]
8. Find the equation of a plane which is at a distance 3√3 units from origin and the normal to which is equally inclined to coordinate axis.
Solution:
As the normal to the plane is equally inclined to the axes we have,
cos α = cos β = cos γ
So, cos2 α + cos2 α + cos2 α = 1
3 cos2 α = 1 ⇒ cos α = ± 1/√3
And, cos α = cos β = cos γ = ± 1/√3
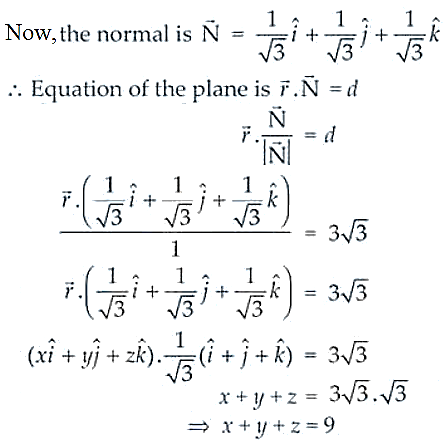
Thus, the equation of the plane is x + y + z = 9
9. Find the equation of the plane which bisects perpendicularly the line joining the points \( A(-2, -1, -3) \) and \( B(1, -3, 3) \) at right angles. \section*
{Solution} \textbf{1. Find the Direction Vector of the Line} The direction vector \( \vec{AB} \) of the line segment joining \( A(-2, -1, -3) \) and \( B(1, -3, 3) \) is: \[ \vec{AB} = \langle 1 – (-2), -3 – (-1), 3 – (-3) \rangle = \langle 3, -2, 6 \rangle \] \textbf{2. Use the Direction Vector as the Normal Vector} Since \( \vec{AB} \) is perpendicular to the plane, it serves as the normal vector \( \vec{n} \) of the plane. Thus, the normal vector is: \[ \vec{n} = \langle 3, -2, 6 \rangle \] \textbf{3. Find the Equation of the Plane} The general equation of a plane with normal vector \( \vec{n} = \langle a, b, c \rangle \) and passing through a point \( (x_1, y_1, z_1) \) is given by: \[ a(x – x_1) + b(y – y_1) + c(z – z_1) = 0 \] Here, \( \vec{n} = \langle 3, -2, 6 \rangle \) and the plane passes through the point \( B(1, -3, 3) \). Substitute these into the plane equation: \[ 3(x – 1) – 2(y + 3) + 6(z – 3) = 0 \] Expand and simplify: \[ 3x – 3 – 2y – 6 + 6z – 18 = 0 \] Combine the constant terms: \[ 3x – 2y + 6z – 27 = 0 \] Thus, the equation of the plane is: \[ 3x – 2y + 6z = 27 \]
10. Find the equation of the plane through the points (2, 1, 0), (3, –2, –2) and (3, 1, 7).
Solution:
Given points are (2, 1, 0), (3, –2, –2) and (3, 1, 7)
As the equation of the plane passing through the points (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) is
(x – 2) (-21) – (y – 1)(7 + 2) + z (3) = 0
-21 (x – 2) – 9(y – 1) + 3z = 0
-21x + 42 – 9y + 9 + 3z = 0
-21x – 9y + 3z + 51 = 0 ⇒ 7x + 3y – z – 17 = 0
Thus, the required equation of plane is 7x + 3y – z – 17 = 0.
11. Find the equations of the two lines through the origin which intersect the line \[ \frac{x – 3}{2} = \frac{y – 3}{1} = \frac{z – 1}{1} \] at angles of \( \frac{\pi}{3} \) each. \section*
{Solution} \textbf{1. Find the Direction Ratios of the Given Line} The given line can be parameterized as: \[ \frac{x – 3}{2} = \frac{y – 3}{1} = \frac{z – 1}{1} = \lambda \] Thus, the direction ratios are: \[ \vec{d}_1 = \langle 2, 1, 1 \rangle \] \textbf{2. Find the Direction Ratios of the Lines Through the Origin} Let the direction ratios of the line through the origin be \( \langle a_2, b_2, c_2 \rangle \). The angle between this line and the given line is \( \frac{\pi}{3} \). The cosine of the angle \( \theta \) between two lines with direction ratios \( \langle a_1, b_1, c_1 \rangle \) and \( \langle a_2, b_2, c_2 \rangle \) is given by: \[ \cos \theta = \frac{a_1 a_2 + b_1 b_2 + c_1 c_2}{\sqrt{a_1^2 + b_1^2 + c_1^2} \sqrt{a_2^2 + b_2^2 + c_2^2}} \] For \( \theta = \frac{\pi}{3} \), \( \cos \frac{\pi}{3} = \frac{1}{2} \). Thus: \[ \frac{2 a_2 + b_2 + c_2}{\sqrt{6} \sqrt{a_2^2 + b_2^2 + c_2^2}} = \frac{1}{2} \] \[ 2 a_2 + b_2 + c_2 = \frac{1}{2} \sqrt{6} \sqrt{a_2^2 + b_2^2 + c_2^2} \] Square both sides to remove the square root: \[ (2 a_2 + b_2 + c_2)^2 = \frac{3}{2} (a_2^2 + b_2^2 + c_2^2) \] \[ 4 a_2^2 + b_2^2 + c_2^2 + 4 a_2 b_2 + 4 a_2 c_2 + 2 b_2 c_2 = \frac{3}{2} (a_2^2 + b_2^2 + c_2^2) \] Multiply through by 2: \[ 8 a_2^2 + 2 b_2^2 + 2 c_2^2 + 8 a_2 b_2 + 8 a_2 c_2 + 4 b_2 c_2 = 3 a_2^2 + 3 b_2^2 + 3 c_2^2 \] Simplify: \[ 5 a_2^2 – b_2^2 – c_2^2 + 8 a_2 b_2 + 8 a_2 c_2 + 4 b_2 c_2 = 0 \] \textbf{3. Find Specific Solutions for \( \langle a_2, b_2, c_2 \rangle \)} To solve, we use: For \( \lambda = -2 \): \[ \langle a_2, b_2, c_2 \rangle = \langle 2(-2) + 3, -2 + 3, -2 \rangle = \langle -1, 1, -2 \rangle \] For \( \lambda = -1 \): \[ \langle a_2, b_2, c_2 \rangle = \langle 2(-1) + 3, -1 + 3, -1 \rangle = \langle 1, 2, -1 \rangle \] \textbf{4. Write the Equations of the Lines} The lines through the origin with these direction ratios are: \[ \frac{x}{-1} = \frac{y}{1} = \frac{z}{-2} \] and \[ \frac{x}{1} = \frac{y}{2} = \frac{z}{-1} \]
12. Find the angle between the lines whose direction cosines are given by the equations l + m + n = 0, l2 + m2 – n2 = 0.
Solution:
Given equations are,
l + m + n = 0 ….. (i)
l2 + m2 – n2 = 0 …. (ii)
From equation (i), we have n = – (l + m)
Putting the value of n is equation (ii), we get
l2 + m2 + [-(l + m)]2 = 0
l2 + m2 – l2 – m2 – 2lm = 0
-2lm = 0
lm = 0 ⇒ (- m – n)m = 0 [Since, l = – m – n]
(m + n)m = 0 ⇒ m = 0 or m = -n
⇒ l = 0 or l = -n
Now, the direction cosines of the two lines are
0, -n, n and -n, 0, n ⇒ 0, -1, 1 and -1, 0, 1
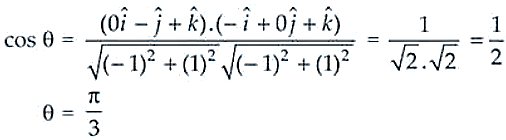
Thus, the required angle π/3.
13. If a variable line in two adjacent positions has direction cosines \((l, m, n)\) and \((l + \delta l, m + \delta m, n + \delta n)\), show that the small angle \(\delta \Theta\) between the two positions is given by: \[ \delta \Theta^2 = \delta l^2 + \delta m^2 + \delta n^2 \] \section*
{Solution} \textbf{1. Initial Condition} The direction cosines of a line satisfy: \[ l^2 + m^2 + n^2 = 1 \] For a line with direction cosines \((l + \delta l, m + \delta m, n + \delta n)\), the condition is: \[ (l + \delta l)^2 + (m + \delta m)^2 + (n + \delta n)^2 = 1 \] \textbf{2. Expand and Simplify} Expanding: \[ (l + \delta l)^2 + (m + \delta m)^2 + (n + \delta n)^2 \] \[ = l^2 + 2l \cdot \delta l + \delta l^2 + m^2 + 2m \cdot \delta m + \delta m^2 + n^2 + 2n \cdot \delta n + \delta n^2 \] \[ = l^2 + m^2 + n^2 + \delta l^2 + \delta m^2 + \delta n^2 + 2(l \cdot \delta l + m \cdot \delta m + n \cdot \delta n) \] \[ = 1 + \delta l^2 + \delta m^2 + \delta n^2 + 2(l \cdot \delta l + m \cdot \delta m + n \cdot \delta n) = 1 \] \[ \delta l^2 + \delta m^2 + \delta n^2 + 2(l \cdot \delta l + m \cdot \delta m + n \cdot \delta n) = 0 \] \[ \delta l^2 + \delta m^2 + \delta n^2 = -2(l \cdot \delta l + m \cdot \delta m + n \cdot \delta n) \] \textbf{3. Cosine of the Angle Between the Two Lines} The cosine of the angle \(\delta \Theta\) is: \[ \cos \delta \Theta = l \cdot (l + \delta l) + m \cdot (m + \delta m) + n \cdot (n + \delta n) \] \[ = l^2 + m^2 + n^2 + l \cdot \delta l + m \cdot \delta m + n \cdot \delta n \] \[ = 1 + l \cdot \delta l + m \cdot \delta m + n \cdot \delta n \] For small angles: \[ \cos \delta \Theta \approx 1 – \frac{\delta \Theta^2}{2} \] \[ 1 + l \cdot \delta l + m \cdot \delta m + n \cdot \delta n \approx 1 – \frac{\delta \Theta^2}{2} \] \[ l \cdot \delta l + m \cdot \delta m + n \cdot \delta n \approx -\frac{\delta \Theta^2}{2} \] \textbf{4. Combine Results} From the earlier result: \[ \delta l^2 + \delta m^2 + \delta n^2 = -2(l \cdot \delta l + m \cdot \delta m + n \cdot \delta n) \] \[ \delta l^2 + \delta m^2 + \delta n^2 \approx \delta \Theta^2 \] Hence: \[ \delta \Theta^2 = \delta l^2 + \delta m^2 + \delta n^2 \]
14. The direction cosines of the line $OA$ (where $O$ is the origin and $A$ is the point $(a, b, c)$) are given by the components of the unit vector in the direction of $OA$.
The direction ratios of $OA$ are $(a, b, c)$. The magnitude of $OA$ is: \[ \sqrt{a^2 + b^2 + c^2} \] Therefore, the direction cosines of $OA$ are: \[ \frac{a}{\sqrt{a^2 + b^2 + c^2}}, \quad \frac{b}{\sqrt{a^2 + b^2 + c^2}}, \quad \frac{c}{\sqrt{a^2 + b^2 + c^2}} \] \subsection*{Equation of the Plane Perpendicular to $OA$ and Passing Through $(a, b, c)$} The plane is perpendicular to $OA$ and passes through the point $A$ with coordinates $(a, b, c)$. The normal to the plane is in the direction of $OA$, which is the vector $\vec{n} = \langle a, b, c \rangle$. The general equation of a plane with normal vector $\vec{n} = \langle a, b, c \rangle$ passing through a point $(x_1, y_1, z_1)$ is: \[ \vec{n} \cdot (\vec{r} – \vec{a}) = 0 \] Here, $\vec{r} = \langle x, y, z \rangle$ and $\vec{a} = \langle a, b, c \rangle$. Substituting $\vec{n}$ and $\vec{a}$: \[ \langle a, b, c \rangle \cdot \left( \langle x, y, z \rangle – \langle a, b, c \rangle \right) = 0 \] \[ a(x – a) + b(y – b) + c(z – c) = 0 \] Simplify this to: \[ ax + by + cz – (a^2 + b^2 + c^2) = 0 \] \[ ax + by + cz = a^2 + b^2 + c^2 \]
15. Let us consider the plane in two different coordinate systems with intercepts \(a\), \(b\), \(c\) and \(a’\), \(b’\), \(c’\), respectively. \subsection*
{Equation of the Plane} In the first system, the plane equation is: \[ \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 \] In the second system, the plane equation is: \[ \frac{x}{a’} + \frac{y}{b’} + \frac{z}{c’} = 1 \] \subsection*{Distance from Origin} The distance from the origin to the plane \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) is: \[ D_1 = \frac{\left| 0 \cdot \frac{1}{a} + 0 \cdot \frac{1}{b} + 0 \cdot \frac{1}{c} – 1 \right|}{\sqrt{\left(\frac{1}{a}\right)^2 + \left(\frac{1}{b}\right)^2 + \left(\frac{1}{c}\right)^2}} \] \[ D_1 = \frac{1}{\sqrt{\frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2}}} \] Similarly, the distance from the origin to the plane \(\frac{x}{a’} + \frac{y}{b’} + \frac{z}{c’} = 1\) is: \[ D_2 = \frac{\left| 0 \cdot \frac{1}{a’} + 0 \cdot \frac{1}{b’} + 0 \cdot \frac{1}{c’} – 1 \right|}{\sqrt{\left(\frac{1}{a’}\right)^2 + \left(\frac{1}{b’}\right)^2 + \left(\frac{1}{c’}\right)^2}} \] \[ D_2 = \frac{1}{\sqrt{\frac{1}{a’^2} + \frac{1}{b’^2} + \frac{1}{c’^2}}} \] Since the distances \(D_1\) and \(D_2\) must be equal, we have: \[ \frac{1}{\sqrt{\frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2}}} = \frac{1}{\sqrt{\frac{1}{a’^2} + \frac{1}{b’^2} + \frac{1}{c’^2}}} \] Squaring both sides, we get: \[ \frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2} = \frac{1}{a’^2} + \frac{1}{b’^2} + \frac{1}{c’^2} \] Thus, the proof is complete. \end{document}
Long Answer (L.A.)
16. Find the foot of the perpendicular from the point \( (2, 3, -8) \) to the line \[ \frac{4 – x}{2} = \frac{y}{6} = \frac{1 – z}{3} = r. \] Also, find the perpendicular distance from the given point to the line. \section*
{Solution} The given line can be expressed in parametric form as: \[ x = 4 – 2r, \] \[ y = 6r, \] \[ z = 1 – 3r. \] Let \( Q(4 – 2r, 6r, 1 – 3r) \) be any point on the line. The point \( P \) is \( (2, 3, -8) \). The vector \( \overrightarrow{PQ} \) from \( P \) to \( Q \) is: \[ \overrightarrow{PQ} = \left( (4 – 2r) – 2, (6r) – 3, (1 – 3r) – (-8) \right) \] \[ \overrightarrow{PQ} = \left( 2 – 2r, 6r – 3, 9 – 3r \right). \] The direction ratios of the line are \( \overrightarrow{d} = (-2, 6, -3) \). For \( \overrightarrow{PQ} \) to be perpendicular to \( \overrightarrow{d} \), their dot product must be zero: \[ \overrightarrow{PQ} \cdot \overrightarrow{d} = 0 \] \[ (2 – 2r) \cdot (-2) + (6r – 3) \cdot 6 + (9 – 3r) \cdot (-3) = 0 \] \[ -4 + 4r + 36r – 18 – 27 + 9r = 0 \] \[ 49r – 49 = 0 \] \[ r = 1. \] Substitute \( r = 1 \) into the parametric equations to get the coordinates of the foot of the perpendicular: \[ Q = (4 – 2 \cdot 1, 6 \cdot 1, 1 – 3 \cdot 1) = (2, 6, -2). \] The vector \( \overrightarrow{PQ} \) for \( r = 1 \) is: \[ \overrightarrow{PQ} = \left( 2 – 2, 6 – 3, -2 – (-8) \right) = (0, 3, 6). \] The length of \( \overrightarrow{PQ} \) is: \[ |\overrightarrow{PQ}| = \sqrt{0^2 + 3^2 + 6^2} = \sqrt{9 + 36} = \sqrt{45} = 3\sqrt{5}. \] \textbf{Summary:} \begin{itemize} \item The foot of the perpendicular from the point \( (2, 3, -8) \) to the line is \( (2, 6, -2) \). \item The perpendicular distance from the point to the line is \( 3\sqrt{5} \) units. \end{itemize}
17. Find the distance of a point (2, 4, –1) from the line
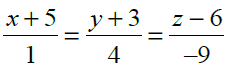
Solution:

18. Find the length and the foot of perpendicular from the point (1, 3/2, 2) to the plane 2x – 2y + 4z + 5 = 0.
Solution:
Given plane is 2x – 2y + 4z + 5 = 0 and point (1, 3/2, 2)
The direction ratios of the normal to the plane are 2, -2, 4
So, the equation of the line passing through (1, 3/2, 2) and direction ratios are equal to the direction ratios of the normal to the plane i.e. 2, -2, 4 is
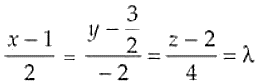
Now, any point in the plane is 2λ + 1, -2λ + 3/2, 4λ + 2
Since, the point lies in the plane, then
2(2λ + 1) – 2(-2λ + 3/2) + 4(4λ + 2) + 5 = 0
4λ + 2 + 4λ – 3 + 16λ + 8 + 5 = 0
24λ + 12 = 0 λ = ½
So, the coordinates of the point in the plane are
2(-1/2) + 1, -2(-1/2) + 3/2, 4(-1/2) + 2 = 0, 5/2, 0
Thus, the foot of the perpendicular is (0, 5/2, 0) and the required length
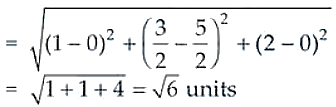
19. Find the equations of the line passing through the point (3,0,1) and parallel to the planes x + 2y = 0 and 3y – z = 0.
Solution:
Given point is (3, 0, 1) and the equation of planes are
x + 2y = 0 …. (i) and 3y – z = 0 …. (ii)
Equation of any line l passing through (3, 0, 1) is
l: (x – 3)/a = (y – 0)/b = (z – 1)/c
Now, the direction ratios of the normal to plane (i) and plane (ii) are (1, 2, 0) and (0, 3, 1).
As the line is parallel to both the planes, we have
1.a + 2.b + 0.c = 0 ⇒ a + 2b + 0c = 0 and
0.a + 3.b – 1.c = 0 ⇒ 0a + 3b – c = 0
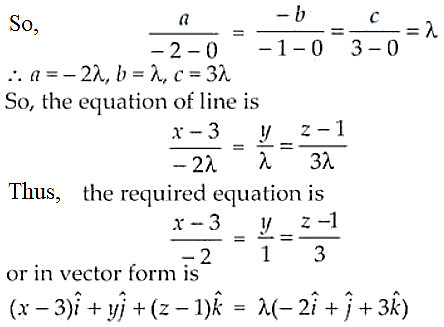
20. Find the vector equation of the plane through the points \( (2, 1, -1) \) and \( (-1, 3, 4) \) and perpendicular to the plane \( x – 2y + 4z = 10 \). The correct option is D: \[ \mathbf{r} \cdot (18 \mathbf{i} + 17 \mathbf{j} + 4 \mathbf{k}) = 49. \] \section*
{Solution} Let the required plane pass through points \( P(2, 1, -1) \) and \( Q(-1, 3, 4) \). The position vectors of these points are: \[ \mathbf{a}_1 = 2 \mathbf{i} + \mathbf{j} – \mathbf{k}, \] \[ \mathbf{a}_2 = -\mathbf{i} + 3 \mathbf{j} + 4 \mathbf{k}. \] The vector \( \overrightarrow{PQ} \) is: \[ \overrightarrow{PQ} = \mathbf{a}_2 – \mathbf{a}_1 = (-\mathbf{i} + 3 \mathbf{j} + 4 \mathbf{k}) – (2 \mathbf{i} + \mathbf{j} – \mathbf{k}), \] \[ \overrightarrow{PQ} = -3 \mathbf{i} + 2 \mathbf{j} + 5 \mathbf{k}. \] Let \( \mathbf{n} \) be the normal vector to the required plane. Since the required plane is perpendicular to the given plane \( x – 2y + 4z = 10 \), its normal vector should be perpendicular to the normal of this given plane. The normal vector to the given plane is: \[ \mathbf{n}_1 = \mathbf{i} – 2 \mathbf{j} + 4 \mathbf{k}. \] The cross product \( \mathbf{n} \) of \( \mathbf{n}_1 \) with \( \overrightarrow{PQ} \) gives the normal vector of the required plane: \[ \mathbf{n} = \mathbf{n}_1 \times \overrightarrow{PQ} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & -2 & 4 \\ -3 & 2 & 5 \end{vmatrix}. \] Calculating the determinant: \[ \mathbf{n} = \mathbf{i} \left( (-2 \cdot 5) – (4 \cdot 2) \right) – \mathbf{j} \left( (1 \cdot 5) – (4 \cdot (-3)) \right) + \mathbf{k} \left( (1 \cdot 2) – ((-2) \cdot (-3)) \right), \] \[ \mathbf{n} = \mathbf{i} (-10 – 8) – \mathbf{j} (5 + 12) + \mathbf{k} (2 – 6), \] \[ \mathbf{n} = -18 \mathbf{i} – 17 \mathbf{j} – 4 \mathbf{k}. \] The plane equation through \( P \) with normal vector \( \mathbf{n} \) is: \[ \mathbf{r} \cdot \mathbf{n} = \mathbf{a}_1 \cdot \mathbf{n}. \] Substituting \( \mathbf{a}_1 = 2 \mathbf{i} + \mathbf{j} – \mathbf{k} \): \[ \mathbf{a}_1 \cdot \mathbf{n} = (2 \mathbf{i} + \mathbf{j} – \mathbf{k}) \cdot (-18 \mathbf{i} – 17 \mathbf{j} – 4 \mathbf{k}), \] \[ \mathbf{a}_1 \cdot \mathbf{n} = 2(-18) + 1(-17) + (-1)(-4), \] \[ \mathbf{a}_1 \cdot \mathbf{n} = -36 – 17 + 4, \] \[ \mathbf{a}_1 \cdot \mathbf{n} = -49. \] Therefore, the equation of the plane is: \[ \mathbf{r} \cdot (-18 \mathbf{i} – 17 \mathbf{j} – 4 \mathbf{k}) = -49. \] Simplifying, the equation of the plane is: \[ \mathbf{r} \cdot (18 \mathbf{i} + 17 \mathbf{j} + 4 \mathbf{k}) = 49. \] Thus, the correct option is D.
21. Find the shortest distance between the lines given by ![]() and
and ![]()
Solution:
Given equations of lines are

22. Find the equation of the plane which is perpendicular to the plane 5x + 3y + 6z + 8 = 0 and which contains the line of intersection of the planes x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0.
Solution:
The given planes are
P1: 5x + 3y + 6z + 8 = 0
P2: x + 2y + 3z – 4 = 0
P3: 2x + y – z + 5 = 0
Now, the equation of the plane passing through the line of intersection of P1 and P3 is
(x + 2y + 3z – 4) + λ(2x + y – z + 5) = 0
(1 + 2λ)x + (2 + λ)y + (3 – λ)z – 4 + 5λ = 0 …. (i)
From the question its understood that plane (i) is perpendicular to P1, then
5(1 + 2λ) + 3(2 + λ) + 6(3 – λ) = 0
5 + 10λ + 6 + 3λ + 18 – 6λ = 0
7λ + 29 = 0
λ = -29/7
Putting the value of ; in equation (i), we get
-15x – 15y + 50z – 28 – 145 = 0
-15x – 15y + 50z – 173 = 0 ⇒ 51x + 15y – 50z + 173 = 0
Thus, the required equation of plane is 51x + 15y – 50z + 173 = 0.
23. If the plane \( ax + by = 0 \) is rotated about its line of intersection with the plane \( z = 0 \) through an angle \( \alpha \), then prove that the equation of the plane in its new position is \[ a x + b y \pm \left( \sqrt{a^2 + b^2} \tan \alpha \right) z = 0. \] \section*
{Solution} The original equation of the plane is: \[ ax + by = 0 \quad \text{(i)} \] To find the equation of the plane after rotation, we need to determine how the plane \( ax + by = 0 \) transforms when rotated about its line of intersection with the plane \( z = 0 \). Consider the equation of the plane in its new position after rotation: \[ \frac{a x}{\cos \alpha \sqrt{a^2 + b^2}} + \frac{b y}{\cos \alpha \sqrt{a^2 + b^2}} \pm z \sin \alpha = 0 \] Simplifying, we get: \[ \frac{a x + b y}{\cos \alpha \sqrt{a^2 + b^2}} \pm z \sin \alpha = 0 \] Multiplying through by \( \cos \alpha \sqrt{a^2 + b^2} \): \[ a x + b y \pm z \sqrt{a^2 + b^2} \tan \alpha = 0 \] Thus, the equation of the rotated plane is: \[ a x + b y \pm \left( \sqrt{a^2 + b^2} \tan \alpha \right) z = 0 \] \section*{Alternate Method} Given the planes: \[ ax + by = 0 \quad \text{(i)} \] \[ z = 0 \quad \text{(ii)} \] The equation of any plane passing through the line of intersection of planes (i) and (ii) can be expressed as: \[ ax + by + k z = 0 \quad \text{(iii)} \] The direction cosines of a normal to plane (i) are: \[ \left( \frac{a}{\sqrt{a^2 + b^2}}, \frac{b}{\sqrt{a^2 + b^2}}, 0 \right) \] Since the angle between planes (i) and (ii) is \( \alpha \), we have: \[ \cos \alpha = \frac{a \cdot a + b \cdot b + k \cdot 0}{\sqrt{a^2 + b^2} \sqrt{a^2 + b^2 + k^2}} \] \[ \cos \alpha = \frac{a^2 + b^2}{\sqrt{a^2 + b^2} \sqrt{a^2 + b^2 + k^2}} \] \[ \cos^2 \alpha = \frac{a^2 + b^2}{a^2 + b^2 + k^2} \] \[ k^2 \cos^2 \alpha = a^2 (1 – \cos^2 \alpha) + b^2 (1 – \cos^2 \alpha) \] \[ k^2 = (a^2 + b^2) \frac{\sin^2 \alpha}{\cos^2 \alpha} \] \[ k = \pm \sqrt{a^2 + b^2} \tan \alpha \] Substituting this value into plane (iii), we get: \[ a x + b y \pm z \sqrt{a^2 + b^2} \tan \alpha = 0 \] Hence, the equation of the plane in its new position is: \[ a x + b y \pm \left( \sqrt{a^2 + b^2} \tan \alpha \right) z = 0 \]
24. If the plane \( ax + by = 0 \) is rotated about its line of intersection with the plane \( z = 0 \) through an angle \( \alpha \), then prove that the equation of the plane in its new position is \[ a x + b y \pm \left( \sqrt{a^2 + b^2} \tan \alpha \right) z = 0. \] \section*
{Solution} The original equation of the plane is: \[ ax + by = 0 \quad \text{(i)} \] To find the equation of the plane after rotation, we need to determine how the plane \( ax + by = 0 \) transforms when rotated about its line of intersection with the plane \( z = 0 \). Consider the equation of the plane in its new position after rotation: \[ \frac{a x}{\cos \alpha \sqrt{a^2 + b^2}} + \frac{b y}{\cos \alpha \sqrt{a^2 + b^2}} \pm z \sin \alpha = 0 \] Simplifying, we get: \[ \frac{a x + b y}{\cos \alpha \sqrt{a^2 + b^2}} \pm z \sin \alpha = 0 \] Multiplying through by \( \cos \alpha \sqrt{a^2 + b^2} \): \[ a x + b y \pm z \sqrt{a^2 + b^2} \tan \alpha = 0 \] Thus, the equation of the rotated plane is: \[ a x + b y \pm \left( \sqrt{a^2 + b^2} \tan \alpha \right) z = 0 \] \section*{Alternate Method} Given the planes: \[ ax + by = 0 \quad \text{(i)} \] \[ z = 0 \quad \text{(ii)} \] The equation of any plane passing through the line of intersection of planes (i) and (ii) can be expressed as: \[ ax + by + k z = 0 \quad \text{(iii)} \] The direction cosines of a normal to plane (i) are: \[ \left( \frac{a}{\sqrt{a^2 + b^2}}, \frac{b}{\sqrt{a^2 + b^2}}, 0 \right) \] Since the angle between planes (i) and (ii) is \( \alpha \), we have: \[ \cos \alpha = \frac{a \cdot a + b \cdot b + k \cdot 0}{\sqrt{a^2 + b^2} \sqrt{a^2 + b^2 + k^2}} \] \[ \cos \alpha = \frac{a^2 + b^2}{\sqrt{a^2 + b^2} \sqrt{a^2 + b^2 + k^2}} \] \[ \cos^2 \alpha = \frac{a^2 + b^2}{a^2 + b^2 + k^2} \] \[ k^2 \cos^2 \alpha = a^2 (1 – \cos^2 \alpha) + b^2 (1 – \cos^2 \alpha) \] \[ k^2 = (a^2 + b^2) \frac{\sin^2 \alpha}{\cos^2 \alpha} \] \[ k = \pm \sqrt{a^2 + b^2} \tan \alpha \] Substituting this value into plane (iii), we get: \[ a x + b y \pm z \sqrt{a^2 + b^2} \tan \alpha = 0 \] Hence, the equation of the plane in its new position is: \[ a x + b y \pm \left( \sqrt{a^2 + b^2} \tan \alpha \right) z = 0 \]
NCERT Exemplar For Class 12 Maths
The NCERT exemplars are an effective study material for scoring higher marks in the examination paper. Students must practise these additional questions for their own benefits, as these are curated by the best subject-matter experts to boost both knowledge and confidence. Students can easily access the ncert exemplar for class 12 maths by visiting our website SimplyAcad and solve all the questions listed to secure maximum marks.
Here are some other NCERT exemplar for class 12 maths:
| NCERT exemplar for class 12 maths Chapter 1 | NCERT exemplar for class 12 maths Chapter 7 |
|---|---|
| NCERT exemplar for class 12 maths Chapter 2 | NCERT exemplar for class 12 maths Chapter 8 |
| NCERT exemplar for class 12 maths Chapter 3 | NCERT exemplar for class 12 maths Chapter 9 |
| NCERT exemplar for class 12 maths Chapter 5 | NCERT exemplar for class 12 maths Chapter 10 |
| NCERT exemplar for class 12 maths Chapter 6 | NCERT exemplar for class 12 maths Chapter 12 |
latest video
news via inbox
Nulla turp dis cursus. Integer liberos euismod pretium faucibua




