NCERT Exemplar for Class 12 Maths Chapter 13

NCERT Exemplar Class 12 Maths Probability are prepared to help students comprehend the concepts, formulas, theorems, etc. thoroughly. Students can always refer to the exemplars for additional practice and revision, this increases the chance of scoring better marks in examinations and also boosts confidence in students. The Ncert exemplar for class 12 maths contains step wise explanations and detailed solved answers which is most effective for students. Regular revisions and practice will ensure that students perform incredibly well in their 12th board examinations.

NCERT exemplar for Class 12 Maths Chapter 13 Probability contains a total of 27 important questions of short and long type. Students can easily access them by scrolling below and practise them consistently to score maximum marks. Our subject matter experts at SimplyAcad have put their best to assist students in learning difficult and complex concepts for their effective learning. Along with this, there are several Ncert exemplar for class 12 maths of all the chapters provided on this platform.

NCERT Exemplar Class 12 Maths Probability – Short Answer (S.A.)

1. For a loaded die, the probabilities of outcomes are given as under:

P(1) = P(2) = 0.2, P(3) = P(5) = P(6) = 0.1 and P(4) = 0.3.

The die is thrown two times. Let A and B be the events, ‘same number each time’, and ‘a total score is 10 or more’, respectively. Determine whether or not A and B are independent.

Solution:

Given that a loaded die is thrown such that

P(1) = P(2) = 0.2, P(3) = P(5) = P(6) = 0.1 and P(4) = 0.3 and die is thrown two times. Also given that:

A = same number each time and

B = Total score is 10 or more.

So, P(A) = [P(1, 1) + P(2, 2) + P(3, 3) + P(4, 4) + P(5, 5) + P(6, 6)]

first, = P(1).P(1) + P(2).P(2) + P(3).P(3) + P(4).P(4) + P(5).P(5) + P(6).P(6).

then, = 0.2 x 0.2 + 0.2 x 0.2 + 0.1 x 0.1 + 0.3 x 0.3 + 0.1 x 0.1 + 0.1 x 0.1.

in last ,= 0.04 + 0.04 + 0.01 + 0.09 + 0.01 + 0.01 = 0.20.

Now, B = [(4, 6), (6, 4), (5, 5), (5, 6), (6, 5), (6, 6)].

P(B) = [P(4).P(6) + P(6).P(4) + P(5).P(5) + P(5).P(6) + P(6).P(5) + P(6).P(6)]

= 0.3 x 0.1 + 0.1 x 0.3 + 0.1 x 0.1 + 0.1 x 0.1 + 0.1 x 0.1 + 0.1 x 0.1

= 0.03 + 0.03 + 0.01 + 0.01 + 0.01 + 0.01 = 0.10

A and B both events will be independent if

P(A ⋂ B) = P(A).P(B) …. (i)

And, here (A ⋂ B) = {(5, 5), (6, 6)}

So, P(A ⋂ B) = P(5, 5) + P(6, 6) = P(5).P(5) + P(6).P(6)

= 0.1 x 0.1 + 0.1 x 0.1 = 0.02

From equation (i) we get,

0.02 = 0.20 x 0.10

0.02 = 0.02

Therefore, A and B are independent events.

2. Refer to Exercise 1 above. If the die were fair, determine whether or not the events A and B are independent.

Solution:

According to the solution of exercise 1, we have

A = {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}and n(6) and n(S) = 6 x 6 = 36

So, P(A) = n(A)/n(S) = 6/36 = 1/6

And, B = {(4, 6), (6, 4), (5, 5), (5, 6), (6, 5), (6, 6)}; n(B) = 6 and n(S) = 36

So, P(B) = n(B)/n(S) = 6/36 = 1/6

Now, A ⋂ B = {(5, 5), (6, 6)}

So, P(A ⋂ B) = 2/36 = 1/18

Hence, if A and B are not independent, then

P(A ⋂ B) ≠ P(A).P(B)

1/18 ≠ 1/6 x 1/6 ⇒ 1/18 ≠ 1/36

Therefore, A and B are not independent events.

3. The probability that at least one of the two events A and B occurs is 0.6. If A and B occur simultaneously with probability 0.3, evaluate

Solution:

W.k.t, A ⋃ B denotes that atleast one of the events occurs and A ⋂ B denotes that two events occur simultaneously.

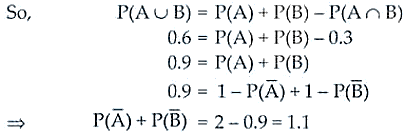
Therefore, the required answer is 1.1.

4. A bag contains 5 red marbles and 3 black marbles. Three marbles are drawn one by one without replacement. What is the probability that at least one of the three marbles drawn is black, given that the first marble is red? \section*

{Solution} Let \( R = \{ \text{5 red marbles} \} \) and \( B = \{ \text{3 black marbles} \} \). For at least one of the three marbles drawn to be black, given that the first marble is red, the following three conditions will be followed: \begin{enumerate} \item[(i)] The second marble is black and the third is red \((E_1)\). \item[(ii)] The second marble is black and the third is also black \((E_2)\). \item[(iii)] The second marble is red and the third is black \((E_3)\). \end{enumerate} \[ P(E_1) = P(R_1) \cdot P(B_1 \mid R_1) \cdot P(R_2 \mid R_1 B_1) = \frac{5}{8} \cdot \frac{3}{7} \cdot \frac{4}{6} = \frac{60}{336} = \frac{5}{28} \] \[ P(E_2) = P(R_1) \cdot P(B_1 \mid R_1) \cdot P(B_2 \mid R_1 B_1) = \frac{5}{8} \cdot \frac{3}{7} \cdot \frac{2}{6} = \frac{30}{336} = \frac{5}{56} \] \[ P(E_3) = P(R_1) \cdot P(R_2 \mid R_1) \cdot P(B_1 \mid R_1 R_2) = \frac{5}{8} \cdot \frac{4}{7} \cdot \frac{3}{6} = \frac{60}{336} = \frac{5}{28} \] \[ \therefore P(E) = P(E_1) + P(E_2) + P(E_3) = \frac{5}{28} + \frac{5}{56} + \frac{5}{28} \] \[ P(E) = \frac{10 + 5 + 10}{56} = \frac{25}{56} \]

5. Two dice are thrown together and the total score is noted. The events E, F and G are ‘a total of 4’, ‘a total of 9 or more’, and ‘a total divisible by 5’, respectively. Calculate P(E), P(F) and P(G) and decide which pairs of events, if any, are independent.

Solution:

If two dice are thrown together, we have

n(S) = 36

Now, let’s consider:

E = A total of 4 = {(2, 2), (1, 3), (3, 1)} ⇒ n(E) = 3

F = A total of 9 or more

= {(3, 6), (6, 3), (5, 4), (4, 5), (5, 5), (4, 6), (6, 4), (5, 6), (6, 5), (6, 6)}

So, n(F) = 10

G = A total divisible by 5

= {(1, 4), (4, 1), (2, 3), (3, 2), (4, 6), (6, 4), (5, 5)}

So, n(G) = 7

It’s seen that (E ⋂ F) = Ø and (E ⋂ G) = Ø

And, (F ⋂ G) = {(4, 6), (6, 4), (5, 5)}

⇒ n(F ⋂ G) = 3 and (E ⋂ F⋂ G) = Ø

Hence, the probabilities if the events are:

As, P(F ⋂ G) ≠ P(F). P(G)

Therefore, there is no pair of independent events.

6. Explain why the experiment of tossing a coin three times is said to have binomial distribution.

Solution:

As the random variable X takes 0, 1, 2, 3, …, n is said to be binomial distribution having parameters n and p, if the probability is given by

P(X = r) = nCr pr qn-r, where q = 1 – p and r = 0, 1, 2, 3, …

Similarly, in case of tossing a coin 3 times, we have

n = 3 and X has the values 0, 1, 2, 3 with p = ½, q = ½.

Therefore, it is said that the experiment of tossing a coin three times have binomial distribution.

7. \textbf{Assertion}: For two events \( A \) and \( B \) such that \( P(A) = P\left(\frac{A}{B}\right) = \frac{1}{4} \) and \( P\left(\frac{B}{A}\right) = \frac{1}{2} \), then \( P\left(\frac{\overline{A}}{B}\right) = \frac{3}{4} \) and \( P\left(\frac{\overline{B}}{A}\right) = \frac{1}{2} \). \textbf{Reason}: If two events \( A \) and \( B \) are independent, then \( P\left(\frac{B}{A}\right) = P(B) \). \section*

{Solution} The correct option is \textbf{A}: Both Assertion and Reason are individually true and Reason is the correct explanation of the Assertion. Since \( P(A) = P\left(\frac{A}{B}\right) = \frac{1}{4} \), \[ \Rightarrow \text{events } A \text{ and } B \text{ are independent}. \] \[ \therefore P(B) = \frac{1}{2} = P\left(\frac{B}{A}\right) \] Now, \[ P\left(\frac{A}{B}\right) = \frac{1}{4} \quad \text{and} \quad P\left(\frac{B}{A}\right) = \frac{1}{2} \] \[ \therefore P\left(\frac{\overline{A}}{B}\right) = 1 – P\left(\frac{A}{B}\right) = 1 – \frac{1}{4} = \frac{3}{4} \] \[ \text{and} \quad P\left(\frac{\overline{B}}{A}\right) = 1 – P\left(\frac{B}{A}\right) = 1 – \frac{1}{2} = \frac{1}{2} \]

8. Three events A, B and C have probabilities 2/5, 1/3 and ½ respectively. Given that P(AÇ C) = 1/5 and P(B Ç C) = ¼, find the values of P(C | B) and P(A’Ç C’).

Solution:

Given, P(A) = 2/5, P(B) = 1/3 and P(C) = ½

P(A Ç C) = 1/5 and P(B Ç C) = ¼

So, P(C/B) = P(B Ç C)/ P(B) = (¼)/ (1/3) = ¾

P(A’ Ç C’) = 1 – P(A ⋃ C)

= 1 – [P(A) + P(C) – P(A Ç C)]

= 1 – [2/5 + ½ – 1/5] = 1 – 7/10 = 3/10

Therefore, the required probabilities are ¾ and 3/10.

9. Let \( E_1 \) and \( E_2 \) be two independent events such that \( P(E_1) = P_1 \) and \( P(E_2) = P_2 \). Describe in words the events whose probabilities are: \begin{enumerate} \item \( P_1 P_2 \) \item \( (1 – P_1) P_2 \) \item \( 1 – (1 – P_1)(1 – P_2) \) \item \( P_1 + P_2 – 2P_1 P_2 \) \end{enumerate} \section*

{Solution} Given that \( P(E_1) = P_1 \) and \( P(E_2) = P_2 \): \begin{enumerate} \item \( P_1 P_2 \Rightarrow P(E_1) \cdot P(E_2) = P(E_1 \cap E_2) \) \textbf{Interpretation:} The probability that both events \( E_1 \) and \( E_2 \) occur. \item \( (1 – P_1) P_2 = P(E_1′) \cdot P(E_2) = P(E_1′ \cap E_2) \) \textbf{Interpretation:} The probability that event \( E_1 \) does not occur but event \( E_2 \) occurs. \item \( 1 – (1 – P_1)(1 – P_2) = 1 – P(E_1′) \cdot P(E_2′) = 1 – P(E_1′ \cap E_2′) = P(E_1 \cup E_2) \) \textbf{Interpretation:} The probability that either event \( E_1 \) or \( E_2 \), or both occur. \item \( P_1 + P_2 – 2P_1 P_2 = P(E_1) + P(E_2) – 2P(E_1 \cap E_2) = P(E_1 \cup E_2) – P(E_1 \cap E_2) \) \textbf{Interpretation:} The probability that either event \( E_1 \) or \( E_2 \) occurs, but not both. \end{enumerate}

10. A discrete random variable \( X \) has the probability distribution as given below: \[ \begin{array}{|c|c|} \hline X & 0.5 \quad 1 \quad 1.5 \quad 2 \\ \hline P(X) & k \quad k \quad \frac{2k}{2} \quad k \\ \hline \end{array} \] Determine the mean of the distribution. \section*

{Solution} We have: \[ \begin{array}{|c|c|} \hline X & 0.5 \quad 1 \quad 1.5 \quad 2 \\ \hline P(X) & k \quad k \quad \frac{2k}{2} \quad k \\ \hline \end{array} \] The probability distribution should satisfy: \[ k + k + k + \frac{2k}{2} = 1 \] \[ k + k + k + k = 1 \] \[ 4k = 1 \quad \Rightarrow \quad k = \frac{1}{4} \] Now, the mean of the distribution \( (\mu) \) is given by: \[ \mu = E(X) = \sum_{i=1}^{n} x_i P(x_i) \] Substitute the values: \[ \mu = 0.5 \cdot k + 1 \cdot k + 1.5 \cdot \frac{2k}{2} + 2 \cdot k \] \[ = 0.5 \cdot \frac{1}{4} + 1 \cdot \frac{1}{4} + 1.5 \cdot \frac{1}{2} + 2 \cdot \frac{1}{4} \] \[ = \frac{0.5}{4} + \frac{1}{4} + \frac{1.5}{2} + \frac{2}{4} \] \[ = \frac{0.5 + 1 + 3 + 2}{4} \] \[ = \frac{6.5}{4} = \frac{13}{8} \] Thus, the mean of the distribution is \( \frac{13}{8} \).

 

12. If X is the number of tails in three tosses of a coin, determine the standard deviation of X.

Solution:

Given, X = 0, 1, 2, 3

P(X = r) = nCr pr qn-r

Where n = 3, p = ½, q = ½ and r = 0, 1, 2, 3

then P(X = 0) = ½ x ½ x ½ = 1/8.

after that P(X = 1) = 3 x ½ x ½ x ½ = 3/8/.

then P(X = 2) = 3 x ½ x ½ x ½ = 3/8.

in last P(X = 3) = ½ x ½ x ½ = 3/8.

The probability distribution table is:

X	0	1	2	3
P(X)	1/8	3/8	3/8	1/8

Now,

E(X) = 0 + 1 x 3/8 + 2 x 3/8 + 3 x 1/8 = 3/8 + 6/8 + 3/8 = 12/8 = 3/2

E(X2) = 0 + 1 x 3/8 + 4 x 3/8 + 9 x 1/8 = 3/8 + 12/8 + 9/8 = 24/8 = 3

W.k.t, Var(X) = E(X2) – [E(X)]2 = 3 – (3/2)2 = 3 – (3/2)2 = 3 – 9/4 = ¾

Thus, the standard deviation = Var(X) = √(¾) = √3/2

 

14. Three dice are thrown at the same time. Find the probability of getting three two’s, if it is known that the sum of the numbers on the dice was six.

Solution:

Given that the dice is thrown three times

So, the sample space n(S) = 63 = 216

Let E1 be the event when the sum of number on the dice was 6 and E2 be the event when three 2’s occur.

E1 = {(1, 1, 4), (1, 2, 3), (1, 4, 1), (2, 1, 3), (2, 2, 2), (2, 3, 1), (3, 1, 2), (3, 2, 1), (4, 1, 1)}

n(E1) =10 and n(E2) = 1 [Since, E2 = (2, 2, 2)]

Thus, P(E2/E1) = P(E1 ⋂ E2)/P(E1) = (1/216)/(10/216) = 1/10.

15. Suppose 10,000 tickets are sold in a lottery each for Re 1. First prize is of Rs 3000 and the second prize is of Rs. 2000. There are three third prizes of Rs. 500 each. If you buy one ticket, what is your expectation.

Solution:

Let’s take X to be the random variable where X = 0, 500, 2000 and 3000

X	0	500	2000	3000
P(X)	9995/10000	3/10000	1/10000	1/10000

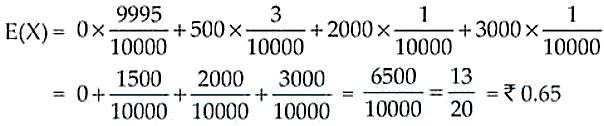
16. A bag contains 4 white and 5 black balls. Another bag contains 9 white and 7 black balls. A ball is transferred from the first bag to the second and then a ball is drawn at random from the second bag. Find the probability that the ball drawn is white.

Solution:

Let’s take W1 and W2 to be two bags containing (4W, 5B) and (9W, 7B) balls respectively.

Let E1 be the event that the transferred ball from the bag W1 to W2 is white and E2 the event that the transferred ball is black.

And, E be the event that the ball drawn from the second bag is white.

So, the probabilities are:

P(E/E1) = 10/17, P(E/E2) = 9/17

P(E1) = 4/9 and P(E2) = 5/9

Now, P(E) = P(E1).P(E/E1) + P(E2).P(E/E2)

= 4/9 x 10/17 + 5/9 x 9/17 = 40/153 + 45/153 = 85/153 = 5/9

Therefore, the required probability is 5/9.

17. Bag I contains 3 black and 2 white balls, Bag II contains 2 black and 4 white balls. A bag and a ball is selected at random. Determine the probability of selecting a black ball.

Solution:

Given that:

Bag 1 has 3B, 2W balls and Bag 2 has 2B, 4W balls.

Let E1 = The event that bag 1 is selected

E2 = The event that bag 2 is selected

And, E = The event that a black ball is selected

Now, the probabilities are:

Therefore, the required probability is 7/15.

18. A box has 5 blue and 4 red balls. One ball is drawn at random and not replaced. Its colour is also not noted. Then another ball is drawn at random. What is the probability of the second ball being blue? \section*

{Solution} Let \( E_1 \) be the event that the first ball drawn is blue, \( E_2 \) be the event that the first ball drawn is red, and \( E \) be the event that the second ball drawn is blue. We need to calculate \( P(E) \), the probability that the second ball drawn is blue. By the law of total probability: \[ P(E) = P(E_1) \cdot P(E | E_1) + P(E_2) \cdot P(E | E_2) \] Now, let’s calculate each term: – \( P(E_1) = \frac{5}{9} \), since there are 5 blue balls out of 9 total balls. – \( P(E_2) = \frac{4}{9} \), since there are 4 red balls out of 9 total balls. – \( P(E | E_1) = \frac{4}{8} = \frac{1}{2} \), since after drawing one blue ball (without replacement), there are 4 blue balls left out of 8 total balls. – \( P(E | E_2) = \frac{5}{8} \), since after drawing one red ball (without replacement), there are still 5 blue balls left out of 8 total balls. Substituting these values: \[ P(E) = \frac{5}{9} \cdot \frac{4}{8} + \frac{4}{9} \cdot \frac{5}{8} \] \[ P(E) = \frac{5}{9} \cdot \frac{1}{2} + \frac{4}{9} \cdot \frac{5}{8} \] \[ P(E) = \frac{5 \times 1}{18} + \frac{4 \times 5}{72} \] \[ P(E) = \frac{5}{18} + \frac{20}{72} \] \[ P(E) = \frac{5}{18} + \frac{5}{18} = \frac{10}{18} = \frac{5}{9} \] Hence, the probability that the second ball drawn is blue is \( \frac{5}{9} \).

23. A lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, what is the probability that there will be at least one defective watch?

Solution:

Given: Total number of watches = 100 and number of defective watches = 10

So, the probability of selecting a detective watch = 10/100 = 1/10

Now,

n = 8, p = 1/10 and q = 1 – 1/10 = 9/10, r ≥ 1

P(X ≥ 1) = 1 – P(x = 0) = 1 – 8C0 (1/10)0(9/10)8 – 0 = 1 – (9/10)8

Therefore, the required probability is 1 – (9/10)8.

24. Consider the probability distribution of a random variable \(X\): \[ \begin{array}{c|c|c|c|c|c} X & 0 & 1 & 2 & 3 & 4 \\ \hline P(X) & 0.1 & 0.25 & 0.3 & 0.2 & 0.15 \\ \end{array} \] Calculate the variance of \(X\). \textbf

{Solution:} We have the following values for \(X\) and \(P(X)\): \[ \begin{array}{c|c|c|c|c|c} X & 0 & 1 & 2 & 3 & 4 \\ \hline P(X) & 0.1 & 0.25 & 0.3 & 0.2 & 0.15 \\ \end{array} \] To calculate the variance, we first need to find \(E(X)\) and \(E(X^2)\). \[ E(X) = \sum_{i=1}^{n} x_i P(x_i) \] Calculating \(X \times P(X)\): \[ \begin{array}{c|c|c|c|c|c} X & 0 & 1 & 2 & 3 & 4 \\ \hline P(X) & 0.1 & 0.25 & 0.3 & 0.2 & 0.15 \\ \hline X \times P(X) & 0 \times 0.1 & 1 \times 0.25 & 2 \times 0.3 & 3 \times 0.2 & 4 \times 0.15 \\ & = 0 & = 0.25 & = 0.6 & = 0.6 & = 0.6 \\ \end{array} \] Summing these values: \[ E(X) = 0 + 0.25 + 0.6 + 0.6 + 0.6 = 2.05 \] Next, calculate \(X^2 \times P(X)\): \[ \begin{array}{c|c|c|c|c|c} X & 0 & 1 & 2 & 3 & 4 \\ \hline P(X) & 0.1 & 0.25 & 0.3 & 0.2 & 0.15 \\ \hline X^2 \times P(X) & 0^2 \times 0.1 & 1^2 \times 0.25 & 2^2 \times 0.3 & 3^2 \times 0.2 & 4^2 \times 0.15 \\ & = 0 & = 0.25 & = 1.2 & = 1.8 & = 2.4 \\ \end{array} \] Summing these values: \[ E(X^2) = 0 + 0.25 + 1.2 + 1.8 + 2.4 = 5.65 \] Now, the variance \(V(X)\) is calculated using the formula: \[ V(X) = E(X^2) – [E(X)]^2 \] Substituting the values: \[ V(X) = 5.65 – (2.05)^2 = 5.65 – 4.2025 = 1.4475 \] Therefore, the variance \(V(X)\) is \(1.4475\).

25. The probability distribution of a random variable X is given below:

X	0	1	2	3
P(X)	k	k/2	k/4	k/8

(i) Determine the value of k.

(ii) Determine P(X £ 2) and P(X > 2)

(iii) Find P(X £ 2) + P (X > 2).

Solution:

(i) W.k.t P(0) + P(1) + P(2) + P(3) = 1

⇒ k + k/2 + k/4 + k/8 = 1

(8k + 4k + 2k + k)/8 = 1

15k = 8

Hence, k = 8/15

(ii) P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)

= k + k/2 + k/4 = 7k/4 = 7/4 x 8/15 = 14/15

And P(X > 2) = P(X = 3) = k/8 = 1/8 x 8/15 = 1/15

(iii) P(X ≤ 2) + P(X ≥ 2) = 14/15 + 1/15 = (14 + 1)/15 = 15/15 = 1

26. For the following probability distribution, determine the standard deviation of the random variable \(X\): \[ \begin{array}{c|c|c|c} X & 2 & 3 & 4 \\ \hline P(X) & 0.2 & 0.5 & 0.3 \\ \end{array} \] \textbf

{Solution:} To find the standard deviation, we first calculate the expected value \(E(X)\) and \(E(X^2)\). \[ E(X) = 2 \times 0.2 + 3 \times 0.5 + 4 \times 0.3 \] \[ E(X) = 0.4 + 1.5 + 1.2 = 3.1 \] Next, we calculate \(E(X^2)\): \[ E(X^2) = 2^2 \times 0.2 + 3^2 \times 0.5 + 4^2 \times 0.3 \] \[ E(X^2) = 4 \times 0.2 + 9 \times 0.5 + 16 \times 0.3 \] \[ E(X^2) = 0.8 + 4.5 + 4.8 = 10.1 \] Now, the variance \( \text{Var}(X) \) is calculated using the formula: \[ \text{Var}(X) = E(X^2) – \left[E(X)\right]^2 \] \[ \text{Var}(X) = 10.1 – (3.1)^2 = 10.1 – 9.61 = 0.49 \] Finally, the standard deviation \( \sigma \) is the square root of the variance: \[ \sigma = \sqrt{\text{Var}(X)} = \sqrt{0.49} = 0.7 \] Hence, the required standard deviation is \( 0.7 \).

 

29. Two biased dice are thrown together. For the first die, \( P(6) = \frac{1}{2} \) and the other scores are equally likely, while for the second die, \( P(1) = \frac{2}{5} \) and the other scores are equally likely. Find the probability distribution of the number of ones seen. \textbf

{Solution:} **For the first die:** Given \( P(6) = \frac{1}{2} \), the probability of not rolling a 6 is: \[ P(\text{not } 6) = 1 – \frac{1}{2} = \frac{1}{2} \] The remaining probability is equally distributed among the numbers 1 through 5: \[ P(1) = P(2) = P(3) = P(4) = P(5) \] Let \( P(1) = p \). Thus: \[ 5p = \frac{1}{2} \implies p = \frac{1}{10} \] Therefore: \[ P(\text{not } 1) = 1 – \frac{1}{10} = \frac{9}{10} \] **For the second die:** Given \( P(1) = \frac{2}{5} \), the probability of not rolling a 1 is: \[ P(\text{not } 1) = 1 – \frac{2}{5} = \frac{3}{5} \] The remaining probability is equally distributed among the numbers 2 through 6. Let \( P(2) = P(3) = P(4) = P(5) = P(6) = q \). Thus: \[ 5q = \frac{3}{5} \implies q = \frac{3}{25} \] **Probability Distribution of \( X \) (the number of ones seen):** Let \( X \) be the number of ones seen. \( X \) can be \( 0, 1, \) or \( 2 \). 1. **For \( X = 0 \):** \[ P(X = 0) = P(\text{not } 1 \text{ on first die}) \times P(\text{not } 1 \text{ on second die}) \] \[ P(X = 0) = \frac{9}{10} \times \frac{3}{5} = \frac{27}{50} = 0.54 \] 2. **For \( X = 1 \):** \[ P(X = 1) = P(\text{not } 1 \text{ on first die}) \times P(1 \text{ on second die}) + P(1 \text{ on first die}) \times P(\text{not } 1 \text{ on second die}) \] \[ P(X = 1) = \frac{9}{10} \times \frac{2}{5} + \frac{1}{10} \times \frac{3}{5} = \frac{18}{50} + \frac{3}{50} = \frac{21}{50} = 0.42 \] 3. **For \( X = 2 \):** \[ P(X = 2) = P(1 \text{ on first die}) \times P(1 \text{ on second die}) \] \[ P(X = 2) = \frac{1}{10} \times \frac{2}{5} = \frac{2}{50} = 0.04 \] **Hence, the probability distribution of \( X \) is:** \[ \begin{array}{c|ccc} X & 0 & 1 & 2 \\ \hline P(X) & 0.54 & 0.42 & 0.04 \end{array} \]

30. Two probability distributions of the discrete random variable X and Y are given below.

X	0	1	2	3
P(X)	1/5	2/5	1/5	1/5
Y	0	1	2	3
P(Y)	1/5	3/10	2/5	1/10

Prove that E(Y2) = 2 E(X).

Solution:

The probability distribution of random variable X is

X	0	1	2	3
P(X)	1/5	2/5	1/5	1/5

We know that,

E(X) 0. 1/5 + 1. 2/5 + 2. 1/5 + 3. 1/5 = 0 + 2/5 + 2/5 + 3/5 = 7/5

For the second probability distribution of random variable Y,

Y	0	1	2	3
P(Y)	1/5	3/10	2/5	1/10

E(Y2) = 0. 1/5 + 1. 3/10 + 4. 2/5 + 9. 1/10

= 0 + 3/10 + 8/5 + 9/10 = 28/10 = 14/5

Now, E(Y2) = 14/5 and 2 E(X) = 2.7/5 = 14/5

Therefore, E(Y2) = 2E(X)

31. A factory produces bulbs. The probability that any one bulb is defective is 1/50 and they are packed in boxes of 10. From a single box, find the probability that

(i) none of the bulbs is defective

(ii) exactly two bulbs are defective

(iii) more than 8 bulbs work properly

Solution:

Let’s assume X to be the random variable denoting a bulb to be defective.

Here, n = 10, p = 1/50, q = 1 – 1/50 = 49/50

We know that, P(X = r) = nCr pr qn – r

(i) None of the bulbs is defective, i.e., r = 0

P(x = 0) = 10C0 (1/50)0(49/50)10 – 0 = (49/50)10

(ii) Exactly two bulbs are defective

So, P(x = 2) = 10C2 (1/50)2(49/50)10 – 2

= 45.498/5010 = 45 x (1/50)10 x 498

(iii) More than 8 bulbs work properly

We can say that less than 2 bulbs are defective

P(x < 2) = P(x = 0) + P(x = 1)

32. Suppose you have two coins which appear identical in your pocket. You know that one is fair and the other is two-headed. If you take one out, toss it, and get a head, what is the probability that it was a fair coin? \textbf

{Solution:} Let: – \( E_1 \) be the event that the fair coin is drawn. – \( E_2 \) be the event that the two-headed coin is drawn. – \( E \) be the event that a head is obtained from the tossed coin. We need to find \( P(E_1 \mid E) \), the probability that the coin is fair given that a head was observed. **Step 1: Calculate \( P(E_1) \) and \( P(E_2) \).** Since there are two coins and they are equally likely to be drawn: \[ P(E_1) = P(E_2) = \frac{1}{2} \] **Step 2: Calculate \( P(E \mid E_1) \) and \( P(E \mid E_2) \).** – For the fair coin: \[ P(E \mid E_1) = \frac{1}{2} \] – For the two-headed coin: \[ P(E \mid E_2) = 1 \] **Step 3: Use Bayes’ Theorem to find \( P(E_1 \mid E) \).** Bayes’ Theorem states: \[ P(E_1 \mid E) = \frac{P(E \mid E_1) \cdot P(E_1)}{P(E)} \] where \( P(E) \) is the total probability of observing a head, calculated as: \[ P(E) = P(E \mid E_1) \cdot P(E_1) + P(E \mid E_2) \cdot P(E_2) \] Substitute the known values: \[ P(E) = \frac{1}{2} \cdot \frac{1}{2} + 1 \cdot \frac{1}{2} = \frac{1}{4} + \frac{1}{2} = \frac{3}{4} \] Thus: \[ P(E_1 \mid E) = \frac{P(E \mid E_1) \cdot P(E_1)}{P(E)} = \frac{\frac{1}{2} \cdot \frac{1}{2}}{\frac{3}{4}} = \frac{\frac{1}{4}}{\frac{3}{4}} = \frac{1}{3} \] Hence, the required probability is \( \frac{1}{3} \).

33. Suppose that 6\% of the people with blood group O are left-handed and 10\% of those with other blood groups are left-handed. 30\% of the people have blood group O. If a left-handed person is selected at random, what is the probability that they will have blood group O? \textbf

{Solution:} Let: – \( E_1 \) be the event that the person has blood group O. – \( E_2 \) be the event that the person has blood group other than O. – \( E \) be the event that the person is left-handed. We are given: – \( P(E_1) = 0.3 \) – \( P(E_2) = 0.7 \) – \( P(E \mid E_1) = 0.06 \) – \( P(E \mid E_2) = 0.10 \) We need to find \( P(E_1 \mid E) \), the probability that a left-handed person has blood group O. Using Bayes’ Theorem: \[ P(E_1 \mid E) = \frac{P(E \mid E_1) \cdot P(E_1)}{P(E)} \] where \( P(E) \) is the total probability of being left-handed: \[ P(E) = P(E \mid E_1) \cdot P(E_1) + P(E \mid E_2) \cdot P(E_2) \] Substitute the known values: \[ P(E) = 0.06 \cdot 0.3 + 0.10 \cdot 0.7 = 0.018 + 0.07 = 0.088 \] Thus: \[ P(E_1 \mid E) = \frac{P(E \mid E_1) \cdot P(E_1)}{P(E)} = \frac{0.06 \cdot 0.3}{0.088} = \frac{0.018}{0.088} = \frac{9}{44} \] Therefore, the probability that a left-handed person will have blood group O is \( \frac{9}{44} \).

34. Two natural numbers r, s are drawn one at a time, without replacement from the set S={1, 2, 3, …., n} . Find P[r £ p|s £ p] , where pÎS.

Solution:

Given, S = {1, 2, 3, …, n}

So, P(r ≤ p/s ≤ p) = P(P ⋂ S)/ P(S)

= p – 1/n x n/(n – 1)

= (p – 1)/(n – 1)

Therefore, the required probability is (p – 1)/(n – 1).

 

36. The random variable X can take only the values 0, 1, 2. Given that P(X = 0) = P (X = 1) = p and that E(X2) = E[X], find the value of p.

Solution:

Given, X = 0, 1, 2 and P(X = 0) = P (X = 1) = p

Let P(X) at X = 2 is x

⇒ p + p + x = 1 ⇒ x = 1 – 2p

Now, we have the following distribution: So,

E(X) = 0.p + 1.p + 2(1 – 2p) = p + 2 – 4p = 2 – 3p

And, E(X2) = 0.p + 1.p + 4(1 – 2p) = p + 4 – 8p = 4 – 7p

Also, given E(X) = E(X2)

2 – 3p = 4 – 7p

4p = 2

p = ½

Therefore, the required value of p is ½.

37. Find the variance of the distribution:

x	0	1	2	3	4	5
P(x)	1/6	5/18	2/9	1/6	1/9	1/18

Solution:

We know that,

Variance(X) = E(X2) – [E(X)]2

Therefore, the required variance is 665/324.

38. A and B throw a pair of dice alternately. A wins the game if he gets a total of 6 and B wins if she gets a total of 7. If A starts the game, find the probability of winning the game by A in the third throw of the pair of dice. \textbf

{Solution:} Let’s first calculate the probabilities of A and B winning in a single throw of the pair of dice: \[ \text{Total number of outcomes when two dice are thrown} = 6 \times 6 = 36 \] \[ \text{A wins with a total of 6} \quad \text{(possible outcomes: (2,4), (1,5), (5,1), (4,2), (3,3))} \implies P(A) = \frac{5}{36} \] \[ \text{B wins with a total of 7} \quad \text{(possible outcomes: (2,5), (1,6), (6,1), (5,2), (3,4), (4,3))} \implies P(B) = \frac{6}{36} = \frac{1}{6} \] The probability of neither A nor B winning in a single throw is: \[ P(A’) = 1 – P(A) = 1 – \frac{5}{36} = \frac{31}{36} \] \[ P(B’) = 1 – P(B) = 1 – \frac{1}{6} = \frac{5}{6} \] We want to find the probability that A wins on the third throw. For A to win on the third throw, the following conditions must be satisfied: 1. Neither A nor B wins in the first throw. 2. Neither A nor B wins in the second throw. 3. A wins on the third throw. The required probability is: \[ P(\text{A wins on the third throw}) = P(A’) \times P(B’) \times P(A) \] Substituting the values: \[ P(\text{A wins on the third throw}) = \left(\frac{31}{36}\right) \times \left(\frac{5}{6}\right) \times \frac{5}{36} \] \[ = \frac{31 \times 5 \times 5}{36 \times 6 \times 36} \] \[ = \frac{775}{7776} \] Hence, the required probability is \( \frac{775}{7776} \).

39. Two dice are tossed. Find whether the following two events A and B are independent:

A = {(x, y) : x + y = 11} B = {(x, y) : x ¹ 5}

where (x, y) denotes a typical sample point.

Solution:

Given, two events A and B are independent such that A = {(x, y) : x + y = 11} B = {(x, y) : x ¹ 5}

Now,

A = {(5, 6), (6, 5)}

B = {(1, 1), (1, 2), (1, 3), (1, 5), (1, 6), (2, 1), (2, 2), (2, 4), (2, 5), (2, 6), (3, 1), (3, 3), (3, 4), (3, 5), (3, 6), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}

n(A) = 2, n(B) = 30 and n(A ⋂ B) = 1

So, P(A) = 2/36 = 1/18 and P(B) = 30/36 = 5/6

Now,

P(A).P(B) = 1/18. 5/6 = 5/108 and P(A ⋂ B) 1/36

As P(A). P(B) ≠ P(A ⋂ B)

Therefore, events A and B are not independent.

 

NCERT Exemplar Class 12 Maths Probability – Long Answer (L.A.)

41. Three bags contain a number of red and white balls as follows:

Bag 1 : 3 red balls, Bag 2 : 2 red balls and 1 white ball

Bag 3 : 3 white balls.

The probability that bag i will be chosen and a ball is selected from it is i/6, i = 1, 2, 3. What is the probability that

(i) a red ball will be selected? (ii) a white ball is selected?

Solution:

Given:

Bag 1 : 3 red balls,

Bag 2 : 2 red balls and 1 white ball

Bag 3 : 3 white balls

Now, let E1, E2 and E3 be the events of choosing Bag 1, Bag 2 and Bag 3 respectively and a ball is drawn from it.

And, we have

P(E1) = 1/6, P(E2) = 2/6 and P(E3) = 3/6

Therefore, the required probabilities are 7/18 and 11/18.

 

Note: Questions are provided by simplyacad for Ncert exemplar for class 12 maths

42. Three bags contain a number of red and white balls as follows: \begin{itemize} \item Bag I: 3 red balls \item Bag II: 2 red balls, 1 white ball \item Bag III: 3 white balls \end{itemize} The probability that bag \(i\) will be chosen and a ball is selected from it is \(\frac{i}{6}\), where \(i = 1, 2, 3\). What is the probability that: \begin{enumerate} \item A red ball will be selected \item A white ball will be selected? \end{enumerate} \textbf

{Solution:} Let \(E_1\), \(E_2\), and \(E_3\) be the events of choosing Bag I, Bag II, and Bag III respectively, and a ball is drawn from it. The probabilities are: \[ P(E_1) = \frac{1}{6}, \quad P(E_2) = \frac{2}{6}, \quad P(E_3) = \frac{3}{6} \] \begin{enumerate} \item Let \(E\) be the event that a red ball is selected. \[ P(E) = P(E_1) \cdot P(E \mid E_1) + P(E_2) \cdot P(E \mid E_2) + P(E_3) \cdot P(E \mid E_3) \] Where: \[ P(E \mid E_1) = 1 \quad \text{(since all balls in Bag I are red)} \] \[ P(E \mid E_2) = \frac{2}{3} \quad \text{(since Bag II contains 2 red balls out of 3)} \] \[ P(E \mid E_3) = 0 \quad \text{(since Bag III contains no red balls)} \] Substituting these values: \[ P(E) = \frac{1}{6} \cdot 1 + \frac{2}{6} \cdot \frac{2}{3} + \frac{3}{6} \cdot 0 \] \[ P(E) = \frac{1}{6} + \frac{4}{18} \] \[ P(E) = \frac{3}{18} + \frac{4}{18} = \frac{7}{18} \] \item Let \(F\) be the event that a white ball is selected. \[ P(F) = 1 – P(E) \] \[ P(F) = 1 – \frac{7}{18} \] \[ P(F) = \frac{18}{18} – \frac{7}{18} = \frac{11}{18} \] \end{enumerate} Hence, the required probabilities are: \begin{itemize} \item Probability of selecting a red ball: \(\frac{7}{18}\) \item Probability of selecting a white ball: \(\frac{11}{18}\) \end{itemize}

43. A shopkeeper sells three types of flower seeds \(A_1\), \(A_2\), and \(A_3\). They are sold as a mixture with proportions \(4:4:2\) respectively. The germination rates of the three types of seeds are \(45\%\), \(60\%\), and \(35\%\) respectively. Calculate the probability that the seed is of type \(A_2\) given that a randomly chosen seed does not germinate. \textbf

{Solution:} The proportion of seeds is given by: \[ A_1 : A_2 : A_3 = 4 : 4 : 2 \] Thus, \[ P(A_1) = \frac{4}{10}, \quad P(A_2) = \frac{4}{10}, \quad P(A_3) = \frac{2}{10} \] Where \(A_1\), \(A_2\), and \(A_3\) are the three types of seeds. Let \(E\) be the event that a seed germinates. The germination rates are: \[ P(E \mid A_1) = \frac{45}{100} = 0.45 \] \[ P(E \mid A_2) = \frac{60}{100} = 0.60 \] \[ P(E \mid A_3) = \frac{35}{100} = 0.35 \] Let \(\overline{E}\) be the event that a seed does not germinate. Thus: \[ P(\overline{E} \mid A_1) = 1 – 0.45 = 0.55 \] \[ P(\overline{E} \mid A_2) = 1 – 0.60 = 0.40 \] \[ P(\overline{E} \mid A_3) = 1 – 0.35 = 0.65 \] We need to find \(P(A_2 \mid \overline{E})\). Using Bayes’ theorem: \[ P(A_2 \mid \overline{E}) = \frac{P(A_2) \cdot P(\overline{E} \mid A_2)}{P(\overline{E})} \] First, compute \(P(\overline{E})\) using the law of total probability: \[ P(\overline{E}) = P(A_1) \cdot P(\overline{E} \mid A_1) + P(A_2) \cdot P(\overline{E} \mid A_2) + P(A_3) \cdot P(\overline{E} \mid A_3) \] \[ P(\overline{E}) = \frac{4}{10} \cdot 0.55 + \frac{4}{10} \cdot 0.40 + \frac{2}{10} \cdot 0.65 \] \[ P(\overline{E}) = \frac{4}{10} \cdot 0.55 + \frac{4}{10} \cdot 0.40 + \frac{2}{10} \cdot 0.65 \] \[ P(\overline{E}) = 0.22 + 0.16 + 0.13 = 0.51 \] Now, calculate \(P(A_2 \mid \overline{E})\): \[ P(A_2 \mid \overline{E}) = \frac{\frac{4}{10} \cdot 0.40}{0.51} \] \[ P(A_2 \mid \overline{E}) = \frac{0.16}{0.51} = \frac{16}{51} \approx 0.314 \] Hence, the probability that the seed is of type \(A_2\) given that it does not germinate is approximately \(0.314\).

44. A letter is known to have come either from \textit{TATA NAGAR} or from \textit{CALCUTTA}. On the envelope, just two consecutive letters “TA” are visible. What is the probability that the letter came from \textit{TATA NAGAR}? \textbf

{Solution:} Let \( E_1 \) be the event that the letter is from \textit{TATA NAGAR} and \( E_2 \) be the event that the letter is from \textit{CALCUTTA}. Let \( E \) be the event that two consecutive letters “TA” are visible. The probabilities of choosing the letter from either city are: \[ P(E_1) = \frac{1}{2}, \quad P(E_2) = \frac{1}{2} \] For \textit{TATA NAGAR}, the set of consecutive letters is: \[ \{TA, AT, TA, AN, NA, AG, GA, AR\} \] Thus, the probability of seeing “TA” given the letter is from \textit{TATA NAGAR} is: \[ P(E \mid E_1) = \frac{\text{Number of “TA”}}{\text{Total pairs}} = \frac{2}{8} = \frac{1}{4} \] For \textit{CALCUTTA}, the set of consecutive letters is: \[ \{CA, AL, LC, CU, UT, TT, TA\} \] Thus, the probability of seeing “TA” given the letter is from \textit{CALCUTTA} is: \[ P(E \mid E_2) = \frac{\text{Number of “TA”}}{\text{Total pairs}} = \frac{1}{7} \] Using Bayes’ Theorem, we need to find \( P(E_1 \mid E) \): \[ P(E_1 \mid E) = \frac{P(E_1) \cdot P(E \mid E_1)}{P(E)} \] First, compute \( P(E) \) using the law of total probability: \[ P(E) = P(E_1) \cdot P(E \mid E_1) + P(E_2) \cdot P(E \mid E_2) \] \[ P(E) = \frac{1}{2} \cdot \frac{1}{4} + \frac{1}{2} \cdot \frac{1}{7} \] \[ P(E) = \frac{1}{8} + \frac{1}{14} \] \[ P(E) = \frac{7 + 4}{56} = \frac{11}{56} \] Now, calculate \( P(E_1 \mid E) \): \[ P(E_1 \mid E) = \frac{\frac{1}{2} \cdot \frac{1}{4}}{\frac{11}{56}} \] \[ P(E_1 \mid E) = \frac{\frac{1}{8}}{\frac{11}{56}} = \frac{56}{88} = \frac{7}{11} \] Thus, the probability that the letter came from \textit{TATA NAGAR} given that two consecutive letters “TA” are visible is \(\frac{7}{11}\).

45. There are two bags, one of which contains 3 black and 4 white balls while the other contains 4 black and 3 white balls. A die is thrown. If it shows up 1 or 3, a ball is taken from the Ist bag; but it shows up any other number, a ball is chosen from the second bag. Find the probability of choosing a black ball.

Solution:

Let E1 be the event of selecting Bag 1 and E2 be the event of selecting Bag 2.

Also, let E3 be the event that black ball is selected

Now,

P(E1) = 2/6 = 1/3 and P(E2) = 1 – 1/3 = 2/3

P(E3/E1) = 3/7 and P(E3/E2) = 4/7

So,

P(E3) = P(E1). P(E3/E1) + P(E2). P(E3/E2)

= 1/3. 3/7 + 2/3. 4/7 = (3 + 8)/ 21 = 11/21

Therefore, the required probability is 11/21.

46. There are three urns containing: \begin{itemize} \item Urn I: 2 white and 3 black balls \item Urn II: 3 white and 2 black balls \item Urn III: 4 white and 1 black ball \end{itemize} Each urn is chosen with equal probability. A ball is drawn at random from the chosen urn and it is found to be white. Find the probability that the ball drawn was from the second urn. \textbf

{Solution:} Let \( E_1 \), \( E_2 \), and \( E_3 \) be the events that a ball is chosen from Urn I, Urn II, and Urn III, respectively. The probabilities of choosing each urn are: \[ P(E_1) = P(E_2) = P(E_3) = \frac{1}{3} \] Let \( W \) be the event that a white ball is drawn. The conditional probabilities of drawing a white ball given the urn are: \[ P(W \mid E_1) = \frac{2}{5} \] \[ P(W \mid E_2) = \frac{3}{5} \] \[ P(W \mid E_3) = \frac{4}{5} \] Using Bayes’ Theorem, we need to find \( P(E_2 \mid W) \): \[ P(E_2 \mid W) = \frac{P(E_2) \cdot P(W \mid E_2)}{P(W)} \] First, compute \( P(W) \) using the law of total probability: \[ P(W) = P(E_1) \cdot P(W \mid E_1) + P(E_2) \cdot P(W \mid E_2) + P(E_3) \cdot P(W \mid E_3) \] \[ P(W) = \frac{1}{3} \cdot \frac{2}{5} + \frac{1}{3} \cdot \frac{3}{5} + \frac{1}{3} \cdot \frac{4}{5} \] \[ P(W) = \frac{2}{15} + \frac{3}{15} + \frac{4}{15} \] \[ P(W) = \frac{9}{15} = \frac{3}{5} \] Now, calculate \( P(E_2 \mid W) \): \[ P(E_2 \mid W) = \frac{\frac{1}{3} \cdot \frac{3}{5}}{\frac{3}{5}} \] \[ P(E_2 \mid W) = \frac{\frac{3}{15}}{\frac{3}{5}} = \frac{\frac{3}{15}}{\frac{9}{15}} = \frac{1}{3} \] Thus, the probability that the white ball drawn came from the second urn is \(\frac{1}{3}\).

47. By examining the chest X-ray, the probability that tuberculosis (TB) is detected when a person is actually suffering from it is \(0.99\). The probability of a healthy person being diagnosed with TB is \(0.001\). In a certain city, \(1\) in \(1000\) people suffers from TB. A person is selected at random and is diagnosed with TB. What is the probability that they actually has TB? \textbf

{Solution:} Let: \begin{itemize} \item \(E_1\) be the event that a person actually has TB. \item \(E_2\) be the event that a person does not have TB. \item \(A\) be the event that a person is diagnosed with TB. \end{itemize} The given probabilities are: \[ P(E_1) = \frac{1}{1000} \] \[ P(E_2) = 1 – P(E_1) = \frac{999}{1000} \] \[ P(A \mid E_1) = 0.99 \] \[ P(A \mid E_2) = 0.001 \] We need to find the probability that a person actually has TB given that they have been diagnosed with it, \(P(E_1 \mid A)\). Using Bayes’ Theorem: \[ P(E_1 \mid A) = \frac{P(E_1) \cdot P(A \mid E_1)}{P(A)} \] First, compute \(P(A)\) using the law of total probability: \[ P(A) = P(E_1) \cdot P(A \mid E_1) + P(E_2) \cdot P(A \mid E_2) \] \[ P(A) = \frac{1}{1000} \cdot 0.99 + \frac{999}{1000} \cdot 0.001 \] \[ P(A) = \frac{0.99}{1000} + \frac{999}{1000} \cdot 0.001 \] \[ P(A) = \frac{0.99}{1000} + \frac{0.999}{1000} \] \[ P(A) = \frac{0.99 + 0.999}{1000} \] \[ P(A) = \frac{1.989}{1000} = 0.001989 \] Now, calculate \(P(E_1 \mid A)\): \[ P(E_1 \mid A) = \frac{P(E_1) \cdot P(A \mid E_1)}{P(A)} \] \[ P(E_1 \mid A) = \frac{\frac{1}{1000} \cdot 0.99}{0.001989} \] \[ P(E_1 \mid A) = \frac{0.00099}{0.001989} \] \[ P(E_1 \mid A) \approx \frac{99}{199} = \frac{55}{111} \approx 0.495 \] Thus, the probability that a person actually has TB given that they are diagnosed with it is approximately \(\frac{55}{111}\).

48. An item is manufactured by three machines A, B and C. Out of the total number of items manufactured during a specified period, 50% are manufactured on A, 30% on B and 20% on C. 2% of the items produced on A and 2% of items produced on B are defective, and 3% of these produced on C are defective. All the items are stored at one godown. One item is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?

Solution:

Let’s consider:

E1 = The event that the item is manufactured on machine A

E2 = The event that the item is manufactured on machine B

E3 = The event that the item is manufactured on machine C

Let H be the event that the selected item is defective.

Thus, by using Baye’s theorem we have

P(E1) = 50/100, P(E2) = 30/100, P(E3) = 20/100

P(H/E1) = 2/100, P(H/E2) = 2/100 and P(H/E3) = 3/100

Therefore, the required probability is 5/11.

49. Let \(X\) be a discrete random variable whose probability distribution is defined as follows: \[ P(X = x) = \begin{cases} k(x + 1) & \text{for } x = 1, 2, 3, 4 \\ 2k x & \text{for } x = 5, 6, 7 \\ 0 & \text{otherwise} \end{cases} \] where \(k\) is a constant. Calculate \(E(X)\). \textbf

{Solution:} First, we need to determine the value of \(k\). Since the sum of all probabilities must equal 1, we have: \[ \sum_{x} P(X = x) = 1 \] The probabilities are: \[ P(X = 1) = k(1 + 1) = 2k \] \[ P(X = 2) = k(2 + 1) = 3k \] \[ P(X = 3) = k(3 + 1) = 4k \] \[ P(X = 4) = k(4 + 1) = 5k \] \[ P(X = 5) = 2k \cdot 5 = 10k \] \[ P(X = 6) = 2k \cdot 6 = 12k \] \[ P(X = 7) = 2k \cdot 7 = 14k \] Adding these probabilities: \[ 2k + 3k + 4k + 5k + 10k + 12k + 14k = 50k \] Setting this equal to 1: \[ 50k = 1 \implies k = \frac{1}{50} \] Now, we calculate \(E(X)\), the expected value of \(X\), using the formula: \[ E(X) = \sum_{x} x \cdot P(X = x) \] Substituting the values: \[ E(X) = 1 \cdot 2k + 2 \cdot 3k + 3 \cdot 4k + 4 \cdot 5k + 5 \cdot 10k + 6 \cdot 12k + 7 \cdot 14k \] \[ E(X) = 2k + 6k + 12k + 20k + 50k + 72k + 98k \] \[ E(X) = 260k \] Substituting \(k = \frac{1}{50}\): \[ E(X) = 260 \cdot \frac{1}{50} = \frac{260}{50} = 5.2 \] Thus, the expected value \(E(X)\) is \(5.2\).

50. The probability distribution of a discrete random variable X is given as under:

X	1	2	4	2A	3A	5A
P(X)	1/2	1/5	3/25	1/10	1/25	1/25

Calculate:

(i) The value of A if E(X) = 2.94

(ii) Variance of X.

Solution:

(i) We know that:

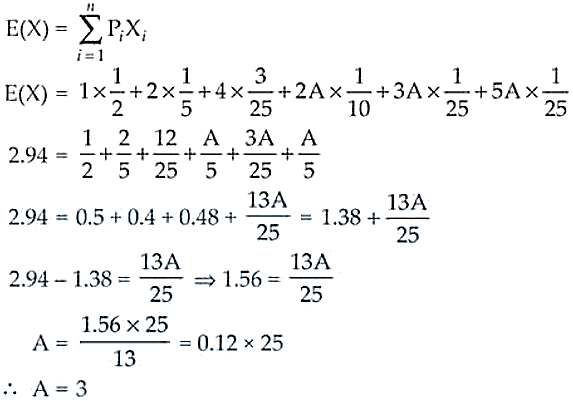
(ii) Now, the distribution becomes

X	1	2	4	6	9	15
P(X)	1/2	1/5	3/25	1/10	1/25	1/25

E(X2) = 1 x ½ + 4 x 1/5 + 16 x 3/25 + 36 x 1/10 + 81 x 1/25 + 225 x 1/25

= ½ + 4/5 + 48/25 + 36/10 + 81/25 + 225/25

= 0.5 + 0.8 + 1.92 + 3.6 + 3.24 + 9 = 19.06

Variance (X) = E(X2) – [E(X)]2

= 19.06 – (2.94)2 = 19.06 – 8.64 = 10.42

51. Let \( X \) be a discrete random variable whose probability distribution is defined as follows: \[ P(X = x) = \begin{cases} k(x + 1) & \text{for } x = 1, 2, 3, 4 \\ 2kx & \text{for } x = 5, 6, 7 \\ 0 & \text{otherwise} \end{cases} \] where \( k \) is a constant. Calculate: \begin{enumerate} \item [(ii)] \( E(X) \) \end{enumerate} \section*

{Solution} To find the constant \( k \), use the fact that the sum of all probabilities must equal 1: \[ \sum_{x} P(X = x) = 1 \] The probabilities are: \[ P(X = 1) = k(1 + 1) = 2k \] \[ P(X = 2) = k(2 + 1) = 3k \] \[ P(X = 3) = k(3 + 1) = 4k \] \[ P(X = 4) = k(4 + 1) = 5k \] \[ P(X = 5) = 2k \cdot 5 = 10k \] \[ P(X = 6) = 2k \cdot 6 = 12k \] \[ P(X = 7) = 2k \cdot 7 = 14k \] Adding these probabilities: \[ 2k + 3k + 4k + 5k + 10k + 12k + 14k = 50k \] Setting this equal to 1: \[ 50k = 1 \implies k = \frac{1}{50} \] Now, compute \( E(X) \), the expected value of \( X \), using: \[ E(X) = \sum_{x} x \cdot P(X = x) \] Substitute the values: \[ E(X) = 1 \cdot 2k + 2 \cdot 3k + 3 \cdot 4k + 4 \cdot 5k + 5 \cdot 10k + 6 \cdot 12k + 7 \cdot 14k \] \[ E(X) = 2k + 6k + 12k + 20k + 50k + 72k + 98k \] \[ E(X) = 260k \] Substitute \( k = \frac{1}{50} \): \[ E(X) = 260 \cdot \frac{1}{50} = \frac{260}{50} = 5.2 \] Thus, the expected value \( E(X) \) is \( 5.2 \).

52. A bag contains (2n + 1) coins. It is known that n of these coins has a head on both sides whereas the rest of the coins are fair. A coin is picked up at random from the bag and is tossed. If the probability that the toss results in a head is 31/42, determine the value of n.

Solution:

Given, n coins are two headed coins and the remaining (n + 1) coins are fair.

Let E1: the event that unfair coin is selected

E2: the event that the fair coin is selected

E: the event that the toss results in a head

So,

P(E1) = n/(2n + 1) and P(E2) = (n + 1)/ (2n +1)

P(E/E1) = 1 (As it’s a sure event)

P(E/E2) = ½

Therefore, the required value of n is 10.

Note: Questions are provided by simplyacad for Ncert exemplar for class 12 maths

53. Two cards are drawn successively without replacement from a well shuffled deck of cards. Find the mean and standard deviation of the random variable \( X \) where \( X \) is the number of aces. \section*

{Solution} Let \( X \) be the random variable which represents the number of aces when two cards are drawn successively without replacement. Then \( X \) can take the values 0, 1, or 2. Let \( E \) denote the event that an ace is drawn, and \( E’ \) denote the event that a non-ace card is drawn. In a deck of 52 cards, there are 4 aces and 48 non-ace cards. \subsection*{For \( X = 0 \)} The probability that both cards drawn are non-aces is: \[ P(X = 0) = P(\text{Both cards drawn are non-aces}) \] \[ P(X = 0) = P(\text{First card drawn is non-ace}) \times P(\text{Second card drawn is non-ace}) \] \[ P(X = 0) = \frac{48}{52} \times \frac{47}{51} = \frac{188}{221} \] \subsection*{For \( X = 1 \)} The probability of drawing exactly one ace is: \[ P(X = 1) = P(\text{One ace is drawn}) \] \[ P(X = 1) = P(\text{First card is ace}) \times P(\text{Second card is non-ace}) + P(\text{First card is non-ace}) \times P(\text{Second card is ace}) \] \[ P(X = 1) = \frac{4}{52} \times \frac{48}{51} + \frac{48}{52} \times \frac{4}{51} = \frac{32}{221} \] \subsection*{For \( X = 2 \)} The probability that both cards drawn are aces is: \[ P(X = 2) = P(\text{Both cards drawn are aces}) \] \[ P(X = 2) = P(\text{First card is ace}) \times P(\text{Second card is ace}) \] \[ P(X = 2) = \frac{4}{52} \times \frac{3}{51} = \frac{1}{221} \] Thus, the probability distribution table is: \[ \begin{array}{c|ccc} X & 0 & 1 & 2 \\ \hline P(X) & \frac{188}{221} & \frac{32}{221} & \frac{1}{221} \end{array} \] \subsection*{Mean \( E(X) \)} \[ E(X) = \sum_{x} x \cdot P(X = x) \] \[ E(X) = 0 \times \frac{188}{221} + 1 \times \frac{32}{221} + 2 \times \frac{1}{221} \] \[ E(X) = \frac{32}{221} + \frac{2}{221} = \frac{34}{221} = \frac{2}{13} \] \subsection*{Variance \( \text{Var}(X) \)} First, compute \( E(X^2) \): \[ E(X^2) = \sum_{x} x^2 \cdot P(X = x) \] \[ E(X^2) = 0^2 \times \frac{188}{221} + 1^2 \times \frac{32}{221} + 2^2 \times \frac{1}{221} \] \[ E(X^2) = \frac{32}{221} + \frac{4}{221} = \frac{36}{221} \] The variance is: \[ \text{Var}(X) = E(X^2) – [E(X)]^2 \] \[ \text{Var}(X) = \frac{36}{221} – \left(\frac{2}{13}\right)^2 \] \[ \left(\frac{2}{13}\right)^2 = \frac{4}{169} \] \[ \text{Var}(X) = \frac{36}{221} – \frac{4}{169} \] \[ \text{Var}(X) = \frac{36 \cdot 169 – 4 \cdot 221}{221 \cdot 169} \] \[ \text{Var}(X) = \frac{6084 – 884}{37309} = \frac{5200}{37309} \] \subsection*{Standard Deviation} \[ \text{Standard Deviation} = \sqrt{\text{Var}(X)} = \sqrt{\frac{5200}{37309}} \approx 0.373 \]

54. A die is tossed twice. A ‘success’ is getting an even number on a toss. Find the variance of the number of successes. \section*

{Solution} Let \( X \) be a random variable representing the number of successes (even numbers) when a die is tossed twice. Then \( X \) can take the values 0, 1, or 2. There are 6 numbers on a die, among which 3 are even and 3 are odd. \subsection*{For \( X = 0 \)} The probability that both numbers are odd (and hence no successes) is: \[ P(X = 0) = P(\text{both numbers are odd}) \] \[ P(X = 0) = P(\text{first number is odd}) \times P(\text{second number is odd}) \] \[ P(X = 0) = \frac{3}{6} \times \frac{3}{6} = \frac{1}{4} \] \subsection*{For \( X = 1 \)} The probability of exactly one success is: \[ P(X = 1) = P(\text{one number is even}) \] \[ P(X = 1) = P(\text{first number is even} \text{ and second number is odd}) + P(\text{first number is odd} \text{ and second number is even}) \] \[ P(X = 1) = \frac{3}{6} \times \frac{3}{6} + \frac{3}{6} \times \frac{3}{6} = \frac{1}{4} + \frac{1}{4} = \frac{1}{2} \] \subsection*{For \( X = 2 \)} The probability that both numbers are even (and hence two successes) is: \[ P(X = 2) = P(\text{both numbers are even}) \] \[ P(X = 2) = P(\text{first number is even}) \times P(\text{second number is even}) \] \[ P(X = 2) = \frac{3}{6} \times \frac{3}{6} = \frac{1}{4} \] Thus, the probability distribution table is: \[ \begin{array}{c|ccc} X & 0 & 1 & 2 \\ \hline P(X) & \frac{1}{4} & \frac{1}{2} & \frac{1}{4} \end{array} \] \subsection*{Mean \( E(X) \)} \[ E(X) = \sum_{x} x \cdot P(X = x) \] \[ E(X) = 0 \times \frac{1}{4} + 1 \times \frac{1}{2} + 2 \times \frac{1}{4} \] \[ E(X) = 0 + \frac{1}{2} + \frac{2}{4} = \frac{1}{2} + \frac{1}{2} = 1 \] \subsection*{Variance \( \text{Var}(X) \)} First, compute \( E(X^2) \): \[ E(X^2) = \sum_{x} x^2 \cdot P(X = x) \] \[ E(X^2) = 0^2 \times \frac{1}{4} + 1^2 \times \frac{1}{2} + 2^2 \times \frac{1}{4} \] \[ E(X^2) = 0 + \frac{1}{2} + \frac{4}{4} = \frac{1}{2} + 1 = \frac{3}{2} \] The variance is: \[ \text{Var}(X) = E(X^2) – [E(X)]^2 \] \[ \text{Var}(X) = \frac{3}{2} – 1 = \frac{1}{2} = 0.5 \] Hence, the variance of the number of successes is \( 0.5 \).

NCERT Exemplar For Class 12 Maths

The NCERT exemplars are an effective study material for scoring higher marks in the examination paper. Students must practise these additional questions for their own benefits, as these are curated by the best subject-matter experts to boost both knowledge and confidence. Students can easily access the ncert exemplar for class 12 maths by visiting our website SimplyAcad and solve all the questions listed to secure maximum marks.

Here are some other NCERT exemplar for class 12 maths:

NCERT exemplar for class 12 maths Chapter 1	NCERT exemplar for class 12 maths Chapter 7
NCERT exemplar for class 12 maths Chapter 2	NCERT exemplar for class 12 maths Chapter 8
NCERT exemplar for class 12 maths Chapter 3	NCERT exemplar for class 12 maths Chapter 9
NCERT exemplar for class 12 maths Chapter 4	NCERT exemplar for class 12 maths Chapter 10
NCERT exemplar for class 12 maths Chapter 5	NCERT exemplar for class 12 maths Chapter 11