NCERT Exemplar for Class 12 Maths Chapter 2

NCERT Exemplar for Class 12 Maths are prepared to help students comprehend the concepts, formulas, theorems, etc. thoroughly. Students can always refer to the exemplars for additional practice and revision, this increases the chance of scoring better marks in examinations and also boosts confidence in students. The NCERT exemplar for class 12 Maths contains step wise explanations and detailed solved answers which is most effective for students. Regular revisions and practice will ensure that students perform incredibly well in their 12th board examinations.

NCERT exemplar for Class 12 Maths Chapter 2 Inverse Trigonometric Functions contains a total of 27 important questions. Students can easily access them by scrolling below and practise them consistently to score maximum marks. Our subject matter experts at SimplyAcad have put their best to assist students in learning difficult and complex concepts for their effective learning. Along with this, there are several NCERT exemplar for class 12 maths of all the chapters provided on this platform.

Access Solutions of the NCERT Exemplar Class 12 Maths Chapter 2 Inverse Trigonometric Function

Short Answer (S.A)

1. Find the value of tan-1 [tan (5π/6)] + cos-1 [cos (13π/6)]

Solution:

We know that,

tan-1 tan x = x, x ∈ (-π/2, π/2)

And, here

tan-1 tan (5π/6) ≠ 5π/6 as 5π/6 ∉ (-π/2, π/2)

Also,

cos-1 cos x = x; x ∈ [0, π]

So,

cos-1 cos (13π/6) ≠ 13π/6 as 13π/6 ∉ [0, π]

Now,

tan-1 [tan (5π/6)] + cos-1 [cos (13π/6)]

first, = tan-1 [tan (π – π /6)] + cos-1 [cos (2π + π/6)]

then, = tan-1 [ -tan π /6] + cos-1 [ -cos (7π/6)]

after that, = – tan-1 [tan π /6] + cos-1 [cos (π/6)]

= – π /6 + π /6

= 0

2. Evaluate: \[ \cos\left[\cos^{-1}\left(-\frac{\sqrt{3}}{2}\right) + \frac{\pi}{6}\right] \] \section*

{Solution} Consider the given expression: \[ \cos\left[\cos^{-1}\left(-\frac{\sqrt{3}}{2}\right) + \frac{\pi}{6}\right] \] We know that: \[ \cos^{-1}\left(-\frac{\sqrt{3}}{2}\right) = \cos^{-1}\left(\cos\left(\frac{5\pi}{6}\right)\right) \] So, the expression becomes: \[ \cos\left[\cos^{-1}\left(\cos\left(\frac{5\pi}{6}\right)\right) + \frac{\pi}{6}\right] \] This simplifies to: \[ \cos\left[\frac{5\pi}{6} + \frac{\pi}{6}\right] \] \[ \cos(\pi) \] \[ -1 \] Hence, the required result is \(-1\).

3. Prove that \[ \cot\left(\frac{\pi}{4} – 2\cot^{-1} 3\right) = 7 \] \section*

{Solution} We have to prove: \[ \cot\left(\frac{\pi}{4} – 2\cot^{-1} 3\right) = 7 \] Starting with: \[ \frac{\pi}{4} – 2\cot^{-1} 3 = \cot^{-1} 7 \] This implies: \[ 2\cot^{-1} 3 = \frac{\pi}{4} – \cot^{-1} 7 \] We know that: \[ 2\tan^{-1} \frac{1}{3} = \frac{\pi}{4} – \tan^{-1} \frac{1}{7} \] Next, applying the identity for the sum of arctangents: \[ 2\tan^{-1} \frac{1}{3} + \tan^{-1} \frac{1}{7} = \frac{\pi}{4} \] Using the tangent addition formula: \[ \tan^{-1}\left(\frac{2/3}{1 – (1/3)^2}\right) + \tan^{-1} \frac{1}{7} = \frac{\pi}{4} \] Simplify the first term: \[ \tan^{-1}\left(\frac{2/3}{8/9}\right) + \tan^{-1} \frac{1}{7} = \frac{\pi}{4} \] \[ \tan^{-1}\left(\frac{3}{4}\right) + \tan^{-1} \frac{1}{7} = \frac{\pi}{4} \] Again, apply the tangent addition formula: \[ \tan^{-1}\left(\frac{\frac{3}{4} + \frac{1}{7}}{1 – \frac{3}{4} \cdot \frac{1}{7}}\right) = \frac{\pi}{4} \] Simplify the expression: \[ \tan^{-1}\left(\frac{21 + 4}{28 – 3}\right) = \frac{\pi}{4} \] \[ \tan^{-1}\left(\frac{25}{25}\right) = \frac{\pi}{4} \] \[ \tan^{-1}(1) = \frac{\pi}{4} \] Since: \[ \tan\left(\frac{\pi}{4}\right) = 1 \] Hence, \[ LHS = RHS \] Thus, the proof is complete.

4. Find the value of \[ \tan^{-1}\left(-\frac{1}{\sqrt{3}}\right) + \cot^{-1}\left(\frac{1}{\sqrt{3}}\right) + \tan^{-1}\left[\sin\left(-\frac{\pi}{2}\right)\right]. \] \section*

{Solution} We have, \[ \tan^{-1}\left(-\frac{1}{\sqrt{3}}\right) + \cot^{-1}\left(\frac{1}{\sqrt{3}}\right) + \tan^{-1}\left[\sin\left(-\frac{\pi}{2}\right)\right] \] \[ = \tan^{-1}\left(\tan \frac{5\pi}{6}\right) + \cot^{-1}\left(\cot \frac{\pi}{3}\right) + \tan^{-1}(-1) \] \[ = \tan^{-1}\left[\tan\left(\pi – \frac{\pi}{6}\right)\right] + \cot^{-1}\left[\cot\left(\frac{\pi}{3}\right)\right] + \tan^{-1}\left(\tan\left(\pi – \frac{\pi}{4}\right)\right) \] \[ = \tan^{-1}\left(-\tan \frac{\pi}{6}\right) + \cot^{-1}\left(\cot \frac{\pi}{3}\right) + \tan^{-1}\left(-\tan \frac{\pi}{4}\right) \] \[ \text{Since, } \tan^{-1}(\tan x) = x \text{ for } x \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right), \] \[ \cot^{-1}(\cot x) = x \text{ for } x \in (0, \pi) \text{ and } \tan^{-1}(-x) = -\tan^{-1}(x), \] we get: \[ = -\frac{\pi}{6} + \frac{\pi}{3} – \frac{\pi}{4} \] Simplify: \[ = \frac{-2\pi}{12} + \frac{4\pi}{12} – \frac{3\pi}{12} \] \[ = \frac{-5\pi + 4\pi}{12} \] \[ = -\frac{\pi}{12} \] Hence, the required value is: \[ -\frac{\pi}{12} \]

5. Find the value of tan-1 (tan 2π/3).

Solution:

We know that,

tan-1 tan x = x, x ∈ (-π/2, π/2)

6. Show that \[ 2 \tan^{-1}(-3) = -\frac{\pi}{2} + \tan^{-1}\left(-\frac{4}{3}\right). \] \section*

{Solution} \textbf{LHS}: \[ 2 \tan^{-1}(-3) = -2 \tan^{-1}(3) \] \[ \text{(since } \tan^{-1}(-x) = -\tan^{-1}(x) \text{ for } x \in \mathbb{R}) \] \[ = -\cos^{-1}\left(\frac{1 – 3^2}{1 + 3^2}\right) \] \[ \text{(since } 2\tan^{-1}x = \cos^{-1}\left(\frac{1-x^2}{1+x^2}\right) \text{ for } x \geq 0) \] \[ = -\cos^{-1}\left(\frac{-8}{10}\right) = -\cos^{-1}\left(-\frac{4}{5}\right) \] \[ = \pi – \cos^{-1}\left(\frac{4}{5}\right) \] \[ \text{(since } \cos^{-1}(-x) = \pi – \cos^{-1}(x) \text{ for } x \in [-1, 1]) \] \[ = -\pi + \cos^{-1}\left(\frac{4}{5}\right) \] Let \(\cos^{-1}\left(\frac{4}{5}\right) = \theta\), so \(\cos \theta = \frac{4}{5}\). Then: \[ \tan \theta = \frac{3}{4} \] \[ \therefore \theta = \tan^{-1}\left(\frac{3}{4}\right) \] Thus: \[ -\pi + \tan^{-1}\left(\frac{3}{4}\right) \] \[ = -\pi + \left(\frac{\pi}{2} – \cot^{-1}\left(\frac{3}{4}\right)\right) \] \[ = -\frac{\pi}{2} – \cot^{-1}\left(\frac{3}{4}\right) \] Since \(\cot^{-1}\left(\frac{3}{4}\right) = \tan^{-1}\left(\frac{4}{3}\right)\), we have: \[ -\frac{\pi}{2} – \tan^{-1}\left(\frac{4}{3}\right) = -\frac{\pi}{2} + \tan^{-1}\left(-\frac{4}{3}\right) \] \[ \text{(since } \tan^{-1}(-x) = -\tan^{-1}(x)) \] \textbf{RHS}: \[ \text{Hence, } \text{LHS} = \text{RHS}. \] \[ \text{Therefore, the equality is proved.} \]

7. Find the real solution of the equation

Solution:

Given equation,

Hence, the real solutions of the given trigonometric equation are 0 and -1.

8. Find the value of the expression \[ \sin\left(2 \tan^{-1}\left(\frac{1}{3}\right)\right) + \cos\left(\tan^{-1}\left(2\sqrt{2}\right)\right). \] \section*

{Solution} Given expression: \[ \sin\left(2 \tan^{-1}\left(\frac{1}{3}\right)\right) + \cos\left(\tan^{-1}\left(2\sqrt{2}\right)\right). \] \subsection*{Step 1: Calculate \( \sin\left(2 \tan^{-1}\left(\frac{1}{3}\right)\right) \)} We know that: \[ \sin\left(2 \tan^{-1}x\right) = \sin\left(\sin^{-1}\left(\frac{2x}{1+x^2}\right)\right), \quad \text{for } x \in \left[-1, 1\right]. \] Therefore, \[ \sin\left(2 \tan^{-1}\left(\frac{1}{3}\right)\right) = \sin\left(\sin^{-1}\left(\frac{2 \times \frac{1}{3}}{1 + \left(\frac{1}{3}\right)^2}\right)\right) \] \[ = \sin\left(\sin^{-1}\left(\frac{\frac{2}{3}}{\frac{10}{9}}\right)\right) = \sin\left(\sin^{-1}\left(\frac{3}{5}\right)\right) = \frac{3}{5}. \] \[ \text{(Since } \sin(\sin^{-1}(x)) = x, \text{ for } x \in \left[-1, 1\right].) \] \subsection*{Step 2: Calculate \( \cos\left(\tan^{-1}\left(2\sqrt{2}\right)\right) \)} We know that: \[ \cos\left(\tan^{-1}x\right) = \cos\left(\cos^{-1}\left(\frac{1}{\sqrt{1+x^2}}\right)\right). \] Therefore, \[ \cos\left(\tan^{-1}\left(2\sqrt{2}\right)\right) = \cos\left(\cos^{-1}\left(\frac{1}{3}\right)\right) = \frac{1}{3}. \] \[ \text{(Since } \cos(\cos^{-1}(x)) = x, \text{ for } x \in \left[-1, 1\right].) \] \subsection*{Step 3: Add the results} \[ \sin\left(2 \tan^{-1}\left(\frac{1}{3}\right)\right) + \cos\left(\tan^{-1}\left(2\sqrt{2}\right)\right) = \frac{3}{5} + \frac{1}{3}. \] Simplifying: \[ \sin\left(2 \tan^{-1}\left(\frac{1}{3}\right)\right) + \cos\left(\tan^{-1}\left(2\sqrt{2}\right)\right) = \frac{9 + 5}{15} = \frac{14}{15}. \] \textbf{Final Answer:} \[ \frac{14}{15}. \]

9. If \[ 2 \tan^{-1}(\cos \theta) = \tan^{-1}\left(2 \csc \theta \right), \] then show that \[ \theta = \frac{\pi}{4}. \] \section*

{Solution} Given: \[ 2 \tan^{-1}(\cos \theta) = \tan^{-1}\left(2 \csc \theta \right). \] Using the identity: \[ 2 \tan^{-1}x = \tan^{-1}\left(\frac{2x}{1-x^2}\right), \quad x \in (-1, 1), \] we can rewrite the left-hand side as: \[ \tan^{-1}\left(\frac{2 \cos \theta}{1 – \cos^2 \theta}\right) = \tan^{-1}\left(2 \csc \theta\right). \] Since the arctan functions are equal, we equate the arguments: \[ \frac{2 \cos \theta}{\sin^2 \theta} = 2 \csc \theta. \] Simplifying, using \( \sin^2 \theta = 1 – \cos^2 \theta \) and \( \csc \theta = \frac{1}{\sin \theta} \): \[ \frac{2 \cos \theta}{\sin^2 \theta} = \frac{2}{\sin \theta}. \] This simplifies to: \[ \frac{\cos \theta}{\sin \theta} = 1. \] Thus: \[ \cot \theta = 1. \] The general solution for \( \cot \theta = 1 \) is: \[ \theta = \frac{\pi}{4}. \] \textbf{Hence, proved.}

10. Show that cos (2 tan-1 1/7) = sin (4 tan-1 1/3).

Solution:

Taking L.H.S, we have

Thus, L.H.S = R.H.S

– Hence proved

11. Solve the equation for \(x\): \[ \cos\left(\tan^{-1} x \right) = \sin\left(\cot^{-1} \frac{3}{4}\right). \] \section*

{Solution} Given: \[ \cos\left(\tan^{-1} x \right) = \sin\left(\cot^{-1} \frac{3}{4}\right). \] We know that: \[ \cos(x) = \sin\left(\frac{\pi}{2} – x\right). \] Therefore, \[ \sin\left(\frac{\pi}{2} – \tan^{-1} x\right) = \sin\left(\cot^{-1} \frac{3}{4}\right). \] Since the sine functions are equal, we equate the arguments: \[ \frac{\pi}{2} – \tan^{-1} x = \cot^{-1} \frac{3}{4}. \] We know that: \[ \frac{\pi}{2} – \tan^{-1} x = \cot^{-1} x. \] So, the equation becomes: \[ \cot^{-1} x = \cot^{-1} \frac{3}{4}. \] Taking the cotangent of both sides: \[ x = \frac{3}{4}. \] \textbf{Hence, the solution is \( x = \frac{3}{4} \).}

12. Prove that

Solution:

Taking L.H.S,

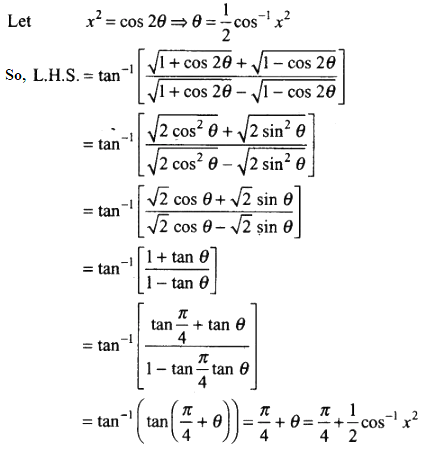
= R.H.S

– Hence Proved

13. Find the simplified form of cos-1 [3/5 cos x + 4/5 sin x], x ∈ [-3π/4, π/4].

Solution:

We have,

cos-1 [3/5 cos x + 4/5 sin x], x ∈ [-3π/4, π/4]

Now, let cos α = 3/5

So, sin α = 4/5 and tan α = 4/3

cos-1 [3/5 cos x + 4/5 sin x]

⇒ cos-1 [3/5 cos x + 4/5 sin x] = cos-1 [cos α cos x + sin α sin x]

= cos-1 [cos (α – x)] = α – x = tan-1 4/3 – x

14. Prove that \[ \sin^{-1}\left(\frac{3}{5}\right) + \sin^{-1}\left(\frac{8}{17}\right) = \sin^{-1}\left(\frac{77}{85}\right). \] \section*

{Solution} We will use the identity: \[ \sin^{-1}a + \sin^{-1}b = \sin^{-1}\left(a\sqrt{1-b^2} + b\sqrt{1-a^2}\right) \] where \(a = \frac{3}{5}\) and \(b = \frac{8}{17}\). Substituting these values, we get: \[ \sin^{-1}\left(\frac{3}{5}\right) + \sin^{-1}\left(\frac{8}{17}\right) = \sin^{-1}\left(\frac{3}{5} \cdot \sqrt{1-\left(\frac{8}{17}\right)^2} + \frac{8}{17} \cdot \sqrt{1-\left(\frac{3}{5}\right)^2}\right). \] First, calculate \( \sqrt{1-\left(\frac{8}{17}\right)^2} \) and \( \sqrt{1-\left(\frac{3}{5}\right)^2} \): \[ \sqrt{1-\left(\frac{8}{17}\right)^2} = \sqrt{1-\frac{64}{289}} = \sqrt{\frac{225}{289}} = \frac{15}{17}, \] \[ \sqrt{1-\left(\frac{3}{5}\right)^2} = \sqrt{1-\frac{9}{25}} = \sqrt{\frac{16}{25}} = \frac{4}{5}. \] Now, substitute these values back: \[ \sin^{-1}\left(\frac{3}{5}\right) + \sin^{-1}\left(\frac{8}{17}\right) = \sin^{-1}\left(\frac{3}{5} \cdot \frac{15}{17} + \frac{8}{17} \cdot \frac{4}{5}\right) = \sin^{-1}\left(\frac{45}{85} + \frac{32}{85}\right). \] Simplify the expression: \[ \sin^{-1}\left(\frac{45}{85} + \frac{32}{85}\right) = \sin^{-1}\left(\frac{77}{85}\right). \] \textbf{Hence Proved.}

15. Show that \[ \sin^{-1}\left(\frac{5}{13}\right) + \cos^{-1}\left(\frac{3}{5}\right) = \tan^{-1}\left(\frac{63}{16}\right). \] \section*

{Solution} We need to prove: \[ \sin^{-1}\left(\frac{5}{13}\right) + \cos^{-1}\left(\frac{3}{5}\right) = \tan^{-1}\left(\frac{63}{16}\right). \] Given: \[ \sin^{-1}\left(\frac{5}{13}\right) = \tan^{-1}\left(\frac{5}{12}\right) \] \[ \cos^{-1}\left(\frac{3}{5}\right) = \tan^{-1}\left(\frac{4}{3}\right) \] \[ \text{(Using the identities: } \sin^{-1}\left(\frac{x}{y}\right) = \tan^{-1}\left(\frac{x}{\sqrt{y^2 – x^2}}\right) \text{ and } \cos^{-1}\left(\frac{x}{y}\right) = \tan^{-1}\left(\frac{\sqrt{y^2 – x^2}}{x}\right)) \] Thus, \[ \sin^{-1}\left(\frac{5}{13}\right) + \cos^{-1}\left(\frac{3}{5}\right) = \tan^{-1}\left(\frac{5}{12}\right) + \tan^{-1}\left(\frac{4}{3}\right) \] Now, use the sum of inverse tangent identity: \[ \tan^{-1}x + \tan^{-1}y = \tan^{-1}\left(\frac{x + y}{1 – xy}\right) \] Substituting the values: \[ \tan^{-1}\left(\frac{5}{12}\right) + \tan^{-1}\left(\frac{4}{3}\right) = \tan^{-1}\left(\frac{\frac{5}{12} + \frac{4}{3}}{1 – \frac{5}{12} \cdot \frac{4}{3}}\right) \] Simplify the expression: \[ = \tan^{-1}\left(\frac{\frac{5}{12} + \frac{16}{12}}{1 – \frac{20}{36}}\right) = \tan^{-1}\left(\frac{\frac{21}{12}}{\frac{16}{36}}\right) = \tan^{-1}\left(\frac{63}{16}\right) \] \textbf{Hence, proved.}

16. Prove that: \[ \tan^{-1}\left(\frac{1}{4}\right) + \tan^{-1}\left(\frac{2}{9}\right) = \sin^{-1}\left(\frac{1}{\sqrt{5}}\right) \] \section*

{Solution} Let’s start with the left-hand side (LHS) of the equation: \[ \tan^{-1}\left(\frac{1}{4}\right) + \tan^{-1}\left(\frac{2}{9}\right) \] Using the sum of inverse tangent identity: \[ \tan^{-1}x + \tan^{-1}y = \tan^{-1}\left(\frac{x + y}{1 – xy}\right) \] Substitute \(x = \frac{1}{4}\) and \(y = \frac{2}{9}\): \[ \tan^{-1}\left(\frac{1}{4}\right) + \tan^{-1}\left(\frac{2}{9}\right) = \tan^{-1}\left(\frac{\frac{1}{4} + \frac{2}{9}}{1 – \frac{1}{4} \times \frac{2}{9}}\right) \] Simplify the expression: \[ = \tan^{-1}\left(\frac{\frac{9 + 8}{36}}{\frac{36 – 2}{36}}\right) = \tan^{-1}\left(\frac{17}{34}\right) = \tan^{-1}\left(\frac{1}{2}\right) \] Now, consider the right-hand side (RHS) of the equation: \[ \sin^{-1}\left(\frac{1}{\sqrt{5}}\right) \] We know: \[ \sin^{-1}\left(\frac{1}{\sqrt{5}}\right) = \tan^{-1}\left(\frac{1}{2}\right) \] Thus: \[ \tan^{-1}\left(\frac{1}{4}\right) + \tan^{-1}\left(\frac{2}{9}\right) = \sin^{-1}\left(\frac{1}{\sqrt{5}}\right) \] \textbf{Hence, proved.}

17. Find the value of \[ 4 \tan^{-1}\left(\frac{1}{5}\right) – \tan^{-1}\left(\frac{1}{239}\right) \] \section*

{Solution} We start with the given expression: \[ 4 \tan^{-1}\left(\frac{1}{5}\right) – \tan^{-1}\left(\frac{1}{239}\right) \] Using the identity for double the inverse tangent: \[ 4 \tan^{-1}\left(\frac{1}{5}\right) = 2 \tan^{-1}\left(\frac{2 \cdot \frac{1}{5}}{1 – \left(\frac{1}{5}\right)^2}\right) = 2 \tan^{-1}\left(\frac{5}{12}\right) \] So, the expression becomes: \[ 2 \tan^{-1}\left(\frac{5}{12}\right) – \tan^{-1}\left(\frac{1}{239}\right) \] Now, using the sum of inverse tangents identity: \[ 2 \tan^{-1}x = \tan^{-1}\left(\frac{2x}{1 – x^2}\right) \] with \( x = \frac{5}{12} \): \[ \tan^{-1}\left(\frac{10/12}{1 – 25/144}\right) = \tan^{-1}\left(\frac{120}{119}\right) \] Thus, the expression reduces to: \[ \tan^{-1}\left(\frac{120}{119}\right) – \tan^{-1}\left(\frac{1}{239}\right) \] Again, applying the difference of inverse tangents identity: \[ \tan^{-1}x – \tan^{-1}y = \tan^{-1}\left(\frac{x-y}{1+xy}\right) \] Substitute \( x = \frac{120}{119} \) and \( y = \frac{1}{239} \): \[ \tan^{-1}\left(\frac{\frac{120}{119} – \frac{1}{239}}{1 + \frac{120}{119} \times \frac{1}{239}}\right) \] Simplify the numerator and denominator: \[ = \tan^{-1}\left(\frac{28680 – 119}{28441 + 120}\right) = \tan^{-1}\left(\frac{28561}{28561}\right) \] Finally: \[ = \tan^{-1}(1) = \frac{\pi}{4} \] \textbf{Hence, the value is } \( \frac{\pi}{4} \).

18. Show that \[ \text{tan}\left(\frac{1}{2} \sin^{-1} \frac{3}{4}\right) = \frac{4 – \sqrt{7}}{3} \] and justify why the other value \(\frac{4 + \sqrt{7}}{3}\) is ignored. \section*

{Solution} We need to show that \[ \text{tan}\left(\frac{1}{2} \sin^{-1} \frac{3}{4}\right) = \frac{4 – \sqrt{7}}{3} \] Given: \[ \text{tan}\left(\frac{1}{2} \sin^{-1} \frac{3}{4}\right) \] Let \(\frac{1}{2} \sin^{-1}\left(\frac{3}{4}\right) = \theta\). Then, \[ \sin^{-1}\left(\frac{3}{4}\right) = 2\theta \] which implies \[ \sin(2\theta) = \frac{3}{4} \] Using the double-angle identity for sine: \[ \sin(2\theta) = \frac{2\tan\theta}{1+\tan^2\theta} \] So, \[ \frac{2\tan\theta}{1+\tan^2\theta} = \frac{3}{4} \] Cross-multiplying: \[ 8\tan\theta = 3 + 3\tan^2\theta \] Rearranging: \[ 3\tan^2\theta – 8\tan\theta + 3 = 0 \] Let \(y = \tan\theta\), then the quadratic equation is: \[ 3y^2 – 8y + 3 = 0 \] Solving this quadratic equation: \[ y = \frac{8 \pm \sqrt{64 – 36}}{6} = \frac{8 \pm \sqrt{28}}{6} = \frac{4 \pm \sqrt{7}}{3} \] Thus, \[ \tan\theta = \frac{4 – \sqrt{7}}{3} \quad \text{or} \quad \tan\theta = \frac{4 + \sqrt{7}}{3} \] Now, \(\theta = \frac{1}{2} \sin^{-1} \left(\frac{3}{4}\right)\) must satisfy: \[ -\frac{\pi}{4} \leq \theta \leq \frac{\pi}{4} \] This means: \[ -1 \leq \tan\theta \leq 1 \] Since \(\frac{4 + \sqrt{7}}{3} > 1\), it is outside the range and must be ignored. Therefore: \[ \tan\left(\frac{1}{2} \sin^{-1} \frac{3}{4}\right) = \frac{4 – \sqrt{7}}{3} \] \textbf{Hence proved.}

19. If \(a_1, a_2, a_3, \dots, a_n\) is an arithmetic progression with common difference \(d\), then evaluate the following expression: \[ \tan\left[\tan^{-1}\left(\frac{d}{1 + \frac{a_1}{a_2}}\right) + \tan^{-1}\left(\frac{d}{1 + \frac{a_2}{a_3}}\right) + \dots + \tan^{-1}\left(\frac{d}{1 + \frac{a_{n-1}}{a_n}}\right)\right] \] \section*

{Solution} Let \[ A = \tan\left[\tan^{-1}\left(\frac{d}{1 + \frac{a_1}{a_2}}\right) + \tan^{-1}\left(\frac{d}{1 + \frac{a_2}{a_3}}\right) + \dots + \tan^{-1}\left(\frac{d}{1 + \frac{a_{n-1}}{a_n}}\right)\right] \] Since \(a_1, a_2, a_3, \dots, a_n\) is an arithmetic progression, we have: \[ d = a_2 – a_1 = a_3 – a_2 = \dots = a_n – a_{n-1} \] This implies that: \[ A = \tan\left[\tan^{-1}\left(\frac{a_2 – a_1}{1 + \frac{a_1}{a_2}}\right) + \tan^{-1}\left(\frac{a_3 – a_2}{1 + \frac{a_2}{a_3}}\right) + \dots + \tan^{-1}\left(\frac{a_n – a_{n-1}}{1 + \frac{a_{n-1}}{a_n}}\right)\right] \] Using the identity: \[ \tan^{-1}(x) – \tan^{-1}(y) = \tan^{-1}\left(\frac{x – y}{1 + xy}\right), \quad \text{where } xy > -1 \] We can express \(A\) as: \[ A = \tan\left[\left(\tan^{-1} a_2 – \tan^{-1} a_1\right) + \left(\tan^{-1} a_3 – \tan^{-1} a_2\right) + \dots + \left(\tan^{-1} a_n – \tan^{-1} a_{n-1}\right)\right] \] This simplifies to: \[ A = \tan\left(\tan^{-1} a_n – \tan^{-1} a_1\right) \] Using the identity: \[ \tan\left(\tan^{-1} x\right) = x, \quad x \in \mathbb{R} \] We get: \[ A = \frac{a_n – a_1}{1 + a_n a_1} \] \textbf{Hence, the required expression evaluates to} \( \frac{a_n – a_1}{1 + a_n a_1} \).

20. Which of the following is the principal value branch of cos-1 x?

(a) [-π/2, π/2] (b) (0, π) (c) [0. π] (d) [0, π] – {π/2}

Solution:

(c) [0. π]

As we know that the principal value branch cos-1 x is [0, π].

21. Which of the following is the principal value branch of cosec-1 x?

(a) (-π/2, π/2) (b) [0, π] – {π/2} (c) [-π/2, π/2] (d) [-π/2, π/2] – {0}

Solution:

(d) [-π/2, π/2] – {0}

As the principal branch of cosec-1 x is [-π/2, π/2] – {0}.

22. If 3 tan-1 x + cot-1 x = π, then x equals

(a) 0 (b) 1 (c) -1 (d) ½

Solution:

(b) 1

Given, 3 tan-1 x + cot-1 x = π

2 tan-1 x + tan-1 x + cot-1 x = π

–> 2 tan-1 x + π/2 = π (As tan-1 + cot-1 = π/2)

Therefore, 2 tan-1 x = π/2

tan-1 x = π/4

x = 1

23. The value of sin-1 cos 33π/5 is

(a) 3π/5 (b) -7π/5 (c) π/10 (d) -π/10

Solution:

(d) -π/10

24. The domain of the function cos-1 (2x – 1) is

(a) [0, 1] (b) [-1, 1] (c) [-1, 1] (d) [0, π]

Solution:

(a) [0, 1]

Since, cos-1 x is defined for x ∈ [-1, 1]

So, f(x) = cos-1 (2x – 1) is defined if

-1 ≤ 2x – 1 ≤ 1

0 ≤ 2x ≤ 2

Hence,

0 ≤ x ≤ 1

25. The domain of the function by f(x) = sin-1 √(x – 1) is

(a) [1, 2] (b) [-1, 1] (c) [0, 1] (d) none of these

Solution:

(a) [1, 2]

We know that, sin-1 x is defined for x ∈ [-1, 1]

So, f(x) = sin-1 √(x – 1) is defined if

0 ≤ √(x – 1) ≤ 1

0 ≤ x – 1 ≤ 1

1 ≤ x ≤ 2

Hence,

x ∈ [1, 2]

26. If cos (sin-1 2/5 + cos-1 x) = 0, then x is equal to

(a) 1/5 (b) 2/5 (c) 0 (d) 1

Solution:

(b) 2/5

Given,

cos (sin-1 2/5 + cos-1 x) = 0

So, this can be rewritten as

sin-1 2/5 + cos-1 x = cos-1 0

sin-1 2/5 + cos-1 x = π/2

cos-1 x = π/2 – sin-1 2/5

cos-1 x = cos-1 2/5 [Since, cos-1 x + sin-1 x = π/2]

Hence,

x = 2/5

27. The value of sin (2 tan-1(0.75)) is equal to

(a) 0.75 (b) 1.5 (c) 0.96 (d) sin 1.5

Solution:

(c) 0.96

We have, sin (2 tan-1(0.75))

NCERT Exemplar For Class 12 Maths

The NCERT exemplars are an effective study material for scoring higher marks in the examination paper. Students must practise these additional questions for their own benefits, as these are curated by the best subject-matter experts to boost both knowledge and confidence. Students can easily access the ncert exemplar for class 12 maths by visiting our website SimplyAcad and solve all the questions listed to secure maximum marks.

Here are some other NCERT exemplar for class 12 maths:

NCERT exemplar for class 12 maths Chapter 1	NCERT exemplar for class 12 maths Chapter 7
NCERT exemplar for class 12 maths Chapter 3	NCERT exemplar for class 12 maths Chapter 8
NCERT exemplar for class 12 maths Chapter 4	NCERT exemplar for class 12 maths Chapter 9
NCERT exemplar for class 12 maths Chapter 5	NCERT exemplar for class 12 maths Chapter 10
NCERT exemplar for class 12 maths Chapter 6	NCERT exemplar for class 12 maths Chapter 11