NCERT Exemplar Class 12 Maths Chapter 3 Matrices
NCERT Exemplar for Class 12 Maths Chapter 3 Matrices
NCERT Exemplar for Class 12 Maths have an incredible set of questions to help students advance their knowledge on the concept of that particular chapter.
This helps students in comprehending the concepts, formulas, theorems, principles,etc. discussed in a better way. Solutions of the NCERT exemplar for class 12 Maths Chapter 3 Matrices meet all the requirements of students and familiarise them with the most asked question. This ensures to boost the confidence in them and get them ready for the upcoming 12th board examination. NCERT exemplar for Class 12 Maths Chapter 3 Matrices contains a total of 50 important questions of short and long type. Students can easily access them by scrolling below and practise them consistently to score maximum marks.
Along with this, there are several NCERT exemplar for class 12 maths of all the chapters provided on this platform.
Access Solutions of the NCERT Exemplar Class 12 Maths Chapter 3 Matrices
Short Answer (S.A.)
1. If a matrix has 28 elements, what are the possible orders it can have? What if it has 13 elements?
Solution:
For a given matrix of order m x n, it has mn elements, where m and n are natural numbers.
Here we have, m x n = 28
(m, n) = {(1, 28), (2, 14), (4, 7), (7, 4), (14, 2), (28, 1)}
So, the possible orders are 1 x 28, 2 x 14, 4 x 7, 7 x 4, 14 x 2, 28 x 1.
Also, if it has 13 elements, then m x n = 13
(m, n) = {(1, 13), (13, 1)}
Thus, the possible orders are 1 x 13, 13 x 1.
2. In the matrix A = , write :
(i) The order of the matrix A
(ii) The number of elements
(iii) Write elements a23, a31, a12
Solution:
For the given matrix,
(i) The order of the matrix A is 3 x 3.
(ii) The number of elements of the matrix = 3 x 3 = 9
(iii) Elements: a23 = x2 – y, a31 = 0, a12 = 1
5. Find values of a and b if A = B, where
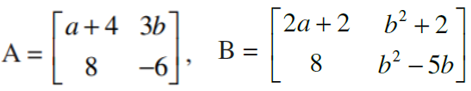
Solution:
Given, matrix A = matrix B
Then their corresponding elements are equal.
So, we have
a11 = b11; a + 4 = 2a + 2 ⇒ a = 2
a12 = b12; 3b = b2 + 2 ⇒ b2 – 3b + 2 = 0 ⇒ b = 1, 2
a22 = b22; -6 = b2 – 5b ⇒ b2 – 5b + 6 = 0 ⇒ b = 2, 3
Hence, a = 2 and b = 2 (common value)
7. If
(i) X + Y
(ii) 2X – 3Y
(iii) A matrix Z such that X + Y + Z is a zero matrix.
Solution:
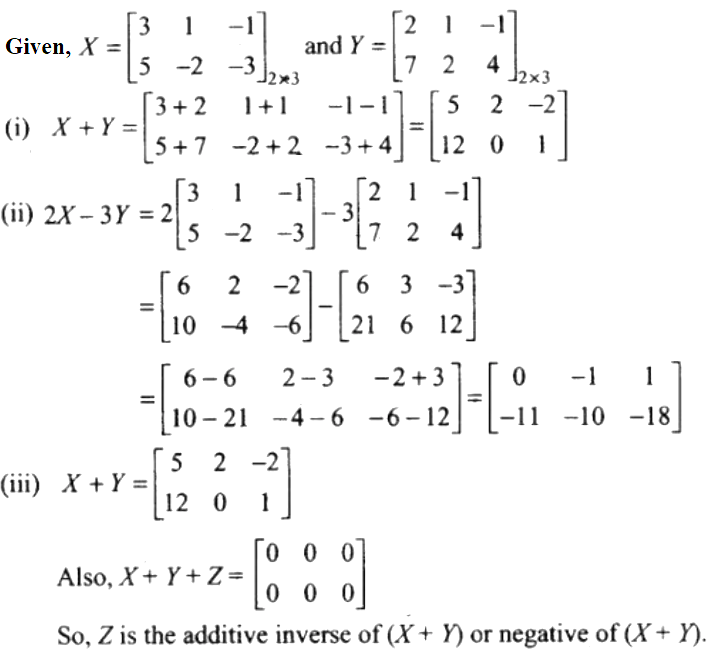
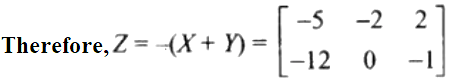
10. Find the value of x if
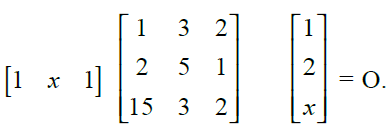
Solution:
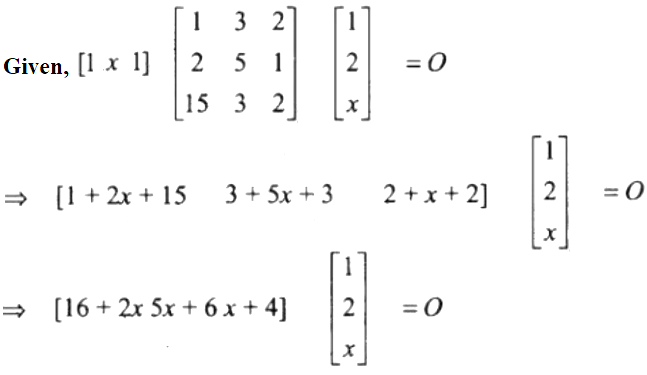
x2 + 16x + 28 = 0
(x + 2) (x + 14) = 0
Therefore, x = -2, -14
13. Find A, if
Solution:
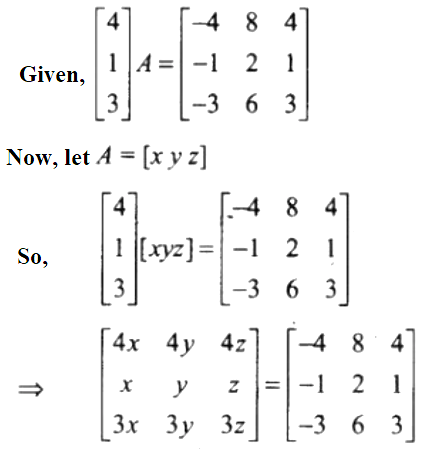
On comparing elements of both sides, we have
4x = -4 ⇒x = -1
4y = 8 ⇒ y = 2
And, 4z = 4 ⇒ z = 1
Therefore, A = [-1 2 1]
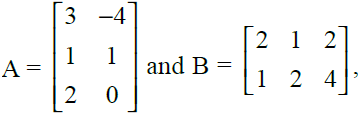
14. If then verify (BA)2 ≠ B2 A2
Solution:
The given matrices A has order 3 x 2 and B has order 2 x 3.
So, BA is defined and will have order 3 x 3.
But, A2 and B2 are not defined as the orders don’t satisfy the multiplication condition.
Hence, (BA)2 ≠ B2 A2
17. Given Is (AB)’ = B’ A’ ?
Solution:

From (i) and (ii), we have
(AB)’ = B’ A’
18. Solve for x and y:
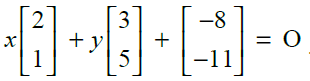
Solution:

Now, we have
2x + 3y – 8 = 0 ….. (1) and
x + 5y – 11 = 0 ….. (2)
On solving the equations (1) and (2), we get
x = 1 and y = 2
19. If X and Y are 2 x 2 matrices, then solve the following matrix equations for X and Y
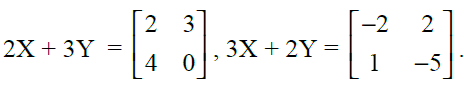
Solution:
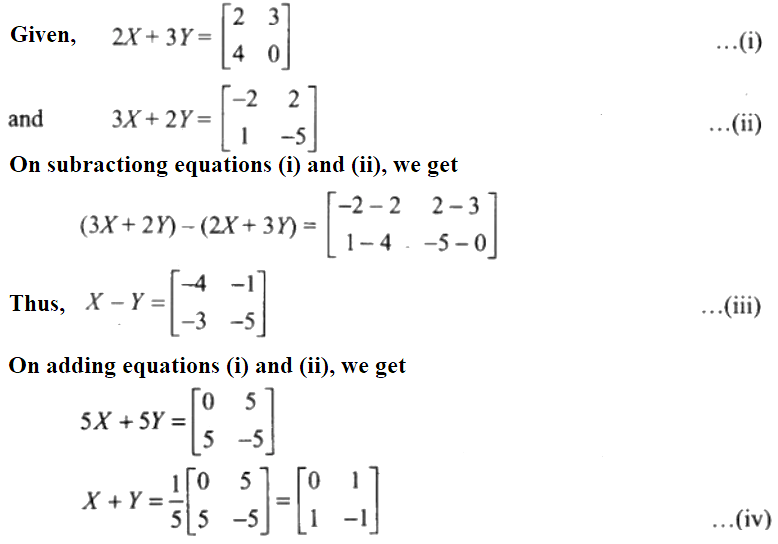
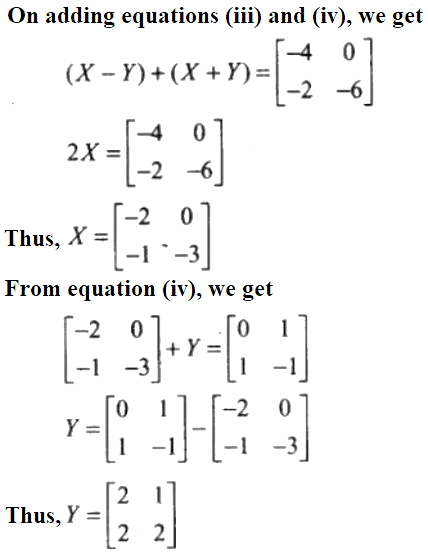
22. If (i) (AB) C = A (BC) (ii) A (B + C) = AB + AC.
Solution:
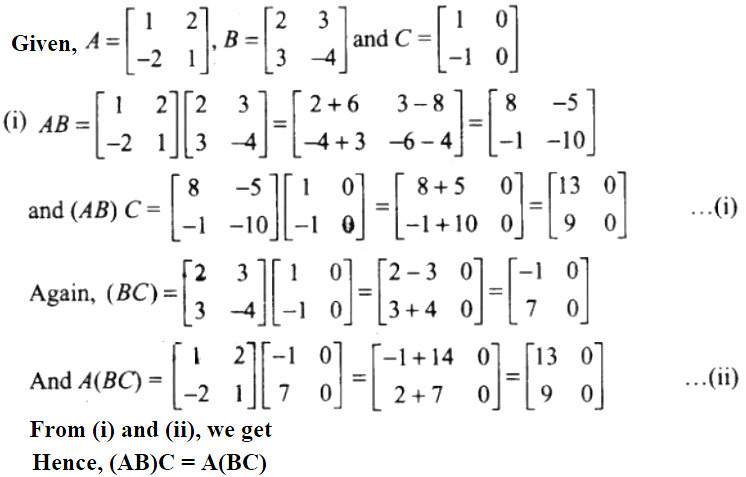

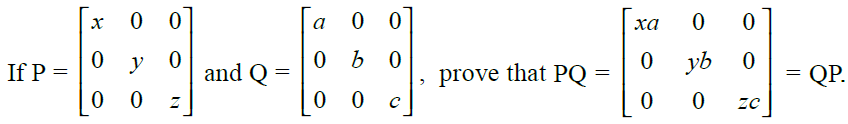
23.
Solution:

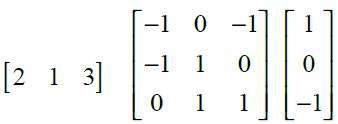
24. If: = A, find A.
Solution:
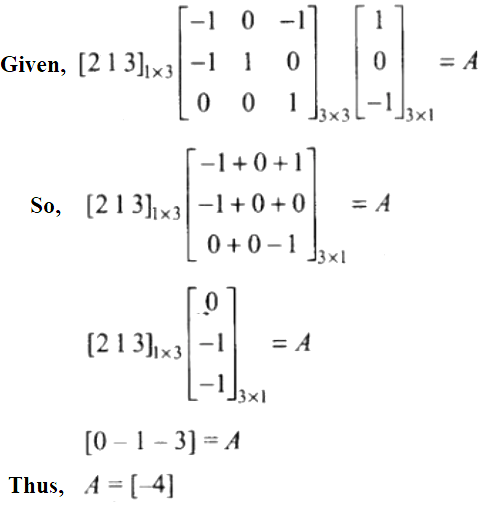
25. If verify that
A (B + C) = (AB + AC).
Solution:
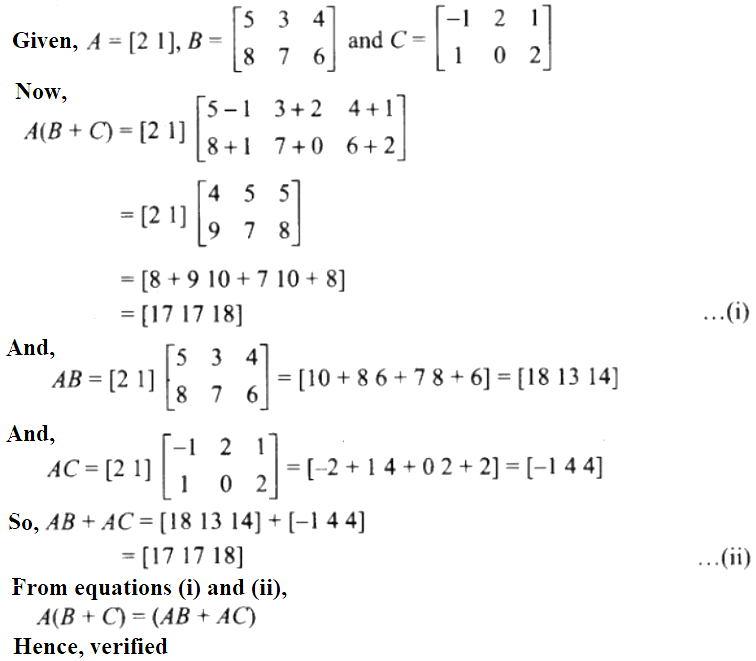
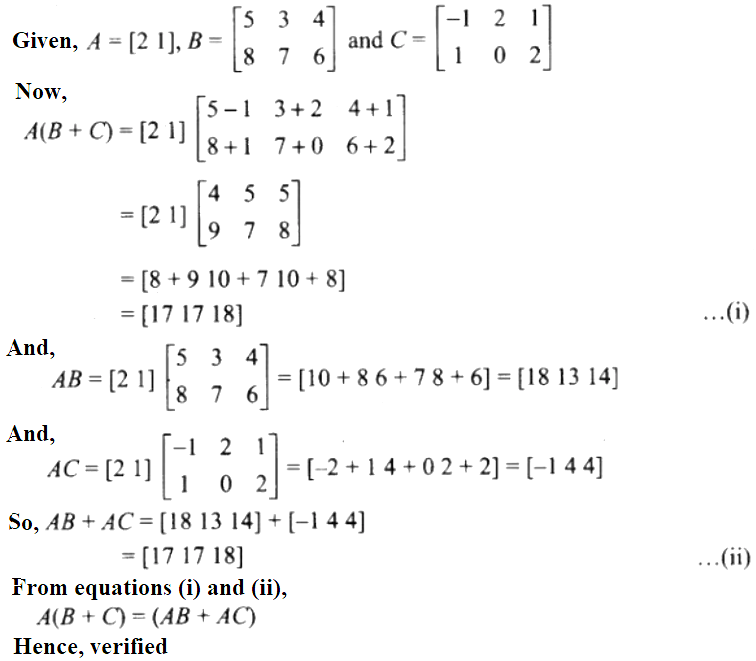
27. If then verify that:
(i) (A¢)¢ = A
(ii) (AB)¢ = B¢A¢
(iii) (kA)¢ = (kA¢).
Solution:


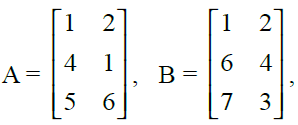
29. Show that A¢A and AA¢ are both symmetric matrices for any matrix A.
Solution:
Let P = A¢A
So, P¢ = (A¢A) ¢
= A¢(A¢)¢ [As (AB) ¢ = B¢A¢]
Hence, A¢A is the symmetric matrix for any matrix A.
Now, let Q = AA¢
So, Q¢ = (AA¢)¢ = (A) ¢ = AA¢ = Q
Hence, AA¢ is the symmetric matrix for any matrix A.
30. Let A and B be square matrices of the order 3 × 3. Is (AB)2 = A2 B2? Give reasons.
Solution:
As, A and B be square matrices of order 3 x 3.
We have, (AB)2 = AB . AB
A(BA)B,
A(AB)B [If AB = BA],
AABB,
A2B2.
Thus, (AB)2 = A2B2 is true only if AB = BA.
31. Show that if A and B are square matrices such that AB = BA, then (A + B)2 = A2 + 2AB + B2.
Solution:
Given, A and B are square matrices such that AB = BA.
So, (A + B)2 = (A + B) . (A + B)
A2 + AB + BA + B2,
then A2 + AB + AB + B2 [Since, AB = BA],
and A2 + 2AB + B2.

Solution:
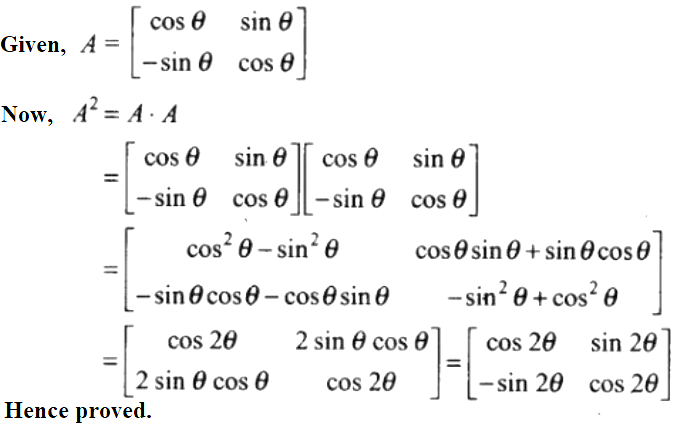
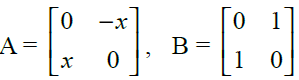
34. If and x2 = –1, then show that (A + B)2 = A2 + B2
Solution:

36. Prove by Mathematical Induction that (A¢)n = (An) ¢, where n ∈ N for any square matrix A.
Solution:
Let P(n): (A¢)n = (An) ¢
So, P(1): (A¢) = (A) ¢
A¢ = A¢
Hence, P(1) is true.
Now, let P(k) = (A¢)k = (Ak) ¢, where k ∈ N
And,
P(k + 1): (A¢)k+1 = (A¢)kA¢
first, = (Ak) ¢A¢
then, = (AAk) ¢
in last, = (Ak+1) ¢
Hence, P(1) is true and whenever P(k) is true P(k + 1) is true.
Therefore, P(n) is true for all n ∈ N.
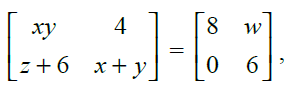
38. If then find values of x, y, z and w.
Solution:
In the given matrix equation,
Comparing the corresponding elements, we get
x + y = 6,
xy = 8,
z + 6 = 0 and
w = 4
From the first two equations, we have
(6 – y) . y = 8
y2 – 6y + 8 = 0
(y – 2) (y – 4) = 0
y = 2 or y = 4
Hence, x = 4 and x = 2
Also, z + 6 = 0
z = -6 and w = 4
Therefore,
x = 2, y = 4 or x = 4, y = 2, z = -6 and w = 4
40. If , then find A2 – 5A – 14I. Hence, obtain A3.
Solution:
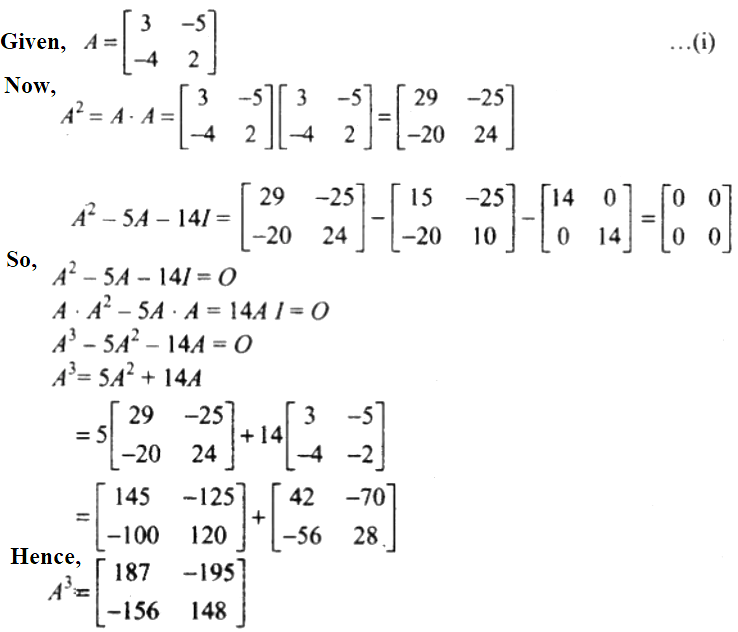
41. Find the value of a, b, c and d, if
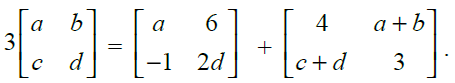
Solution:
Given,
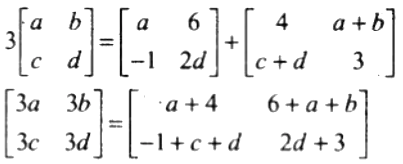
Now,
3a = a + 4 ⇒ a = 2
3b = 6 + a + b
3b – b = 8
⇒ b = 4
And,
3d = 3 + 2d
⇒ d = 3
And,
3c = c + d – 1
2c = 3 – 1 = 2
⇒ c = 1
Hence,
a = 2, b = 4, c = 1 and d = 3
42. Find the matrix A such that
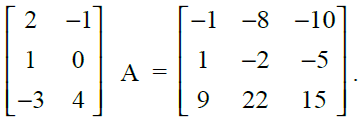
Solution:
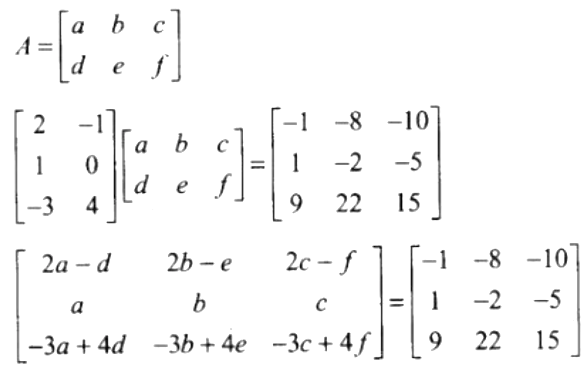
Let,
Now, by equality of matrices, we get
a = 1, b = -2, c = -5
And,
2a – d = -1 ⇒ d = 2a + 1 = 3;
2b – e = -8 ⇒ e = 2(-2) + 8 = 4
2c – f = -10 ⇒ f = 2c + 10 = 0
Thus,
43. If A = find A2 + 2A + 7I.
Solution:
Given,
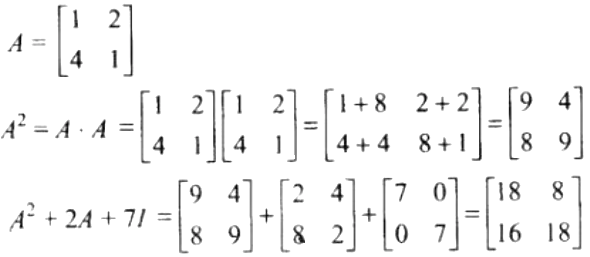
44. If A = and A-1 = A’, find the value of a.
Solution:
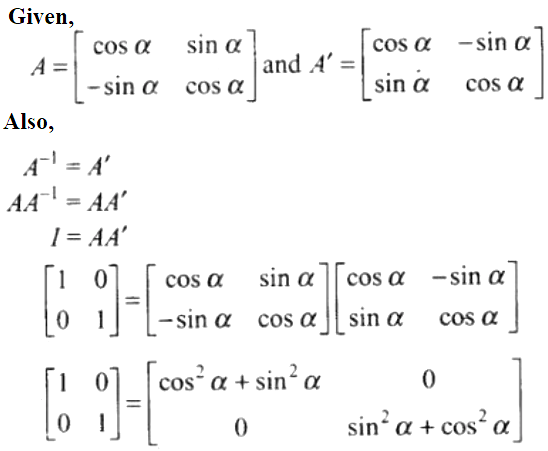
By using the equality of matrices, we get
cos2 α + sin2 α = 1, which is true for all real values of α.
45. If the matrix \[ A = \begin{bmatrix} 0 & a & 3 \\ 2 & b & -1 \\ c & 1 & 0 \end{bmatrix} \] is a skew-symmetric matrix, find the values of \(a\), \(b\), and \(c\). \section*
{Solution} Let \[ A = \begin{bmatrix} 0 & a & 3 \\ 2 & b & -1 \\ c & 1 & 0 \end{bmatrix} \] For a skew-symmetric matrix, the condition is: \[ A^T = -A \] The transpose of \(A\) is: \[ A^T = \begin{bmatrix} 0 & 2 & c \\ a & b & 1 \\ 3 & -1 & 0 \end{bmatrix} \] Applying the skew-symmetric condition \(A^T = -A\): \[ \begin{bmatrix} 0 & 2 & c \\ a & b & 1 \\ 3 & -1 & 0 \end{bmatrix} = \begin{bmatrix} 0 & -a & -3 \\ -2 & -b & -1 \\ -c & -1 & 0 \end{bmatrix} \] By comparing corresponding elements, we get: \[ -a = 2 \quad \Rightarrow \quad a = -2 \] \[ -c = c \quad \Rightarrow \quad 2c = 0 \quad \Rightarrow \quad c = 0 \] \[ -b = -1 \quad \Rightarrow \quad b = 1 \] Thus, the values are: \[ a = -2, \quad b = 1, \quad c = 0 \]
46. If P (x) = then show that P (x) . P (y) = P (x + y) = P (y) . P (x).
Solution:
Given,


47. If A is square matrix such that A2 = A, show that (I + A)3 = 7A + I.
Solution:
We know that,
A . I = I . A
So, A and I are commutative.
Thus, we can expand (I + A)3 like real numbers expansion.
So, (I + A)3 = I3 + 3I2A + 3IA2 + A3
- = I + 3IA + 3A2 + AA2 (As In = I, n ∈ N)
- = I + 3A + 3A + AA
- = I + 3A + 3A + A2 = I + 3A + 3A + A = I + 7A
48. If A, B are square matrices of same order and B is a skew-symmetric matrix, show that A¢BA is skew symmetric.
Solution:
Given, A and B are square matrices such that B is a skew-symmetric matrix
So, B¢ = -B
Now, we have to prove that A¢BA is a skew-symmetric matrix.
(A¢BA) ¢ = A¢B¢ (A¢)¢ [Since, (AB) ¢ = B¢A¢]
= A¢ (-B)A
= -A¢BA
Hence, A¢BA is a skew-symmetric matrix.
Long Answer (L.A)
50. Find x, y, z if A = satisfies A¢ = A-1.
Solution:
Matrix A is such that A¢ = A-1
AA¢ = I

NCERT Exemplar For Class 12 Maths
The NCERT exemplars are an effective study material for scoring higher marks in the examination paper. Students must practise these additional questions for their own benefits, as these are curated by the best subject-matter experts to boost both knowledge and confidence. Students can easily access the ncert exemplar for class 12 maths by visiting our website SimplyAcad and solve all the questions listed to secure maximum marks.
Here are some other NCERT exemplar for class 12 maths:
| NCERT exemplar for class 12 maths Chapter 1 | NCERT exemplar for class 12 maths Chapter 7 |
|---|---|
| NCERT exemplar for class 12 maths Chapter 2 | NCERT exemplar for class 12 maths Chapter 8 |
| NCERT exemplar for class 12 maths Chapter 4 | NCERT exemplar for class 12 maths Chapter 9 |
| NCERT exemplar for class 12 maths Chapter 5 | NCERT exemplar for class 12 maths Chapter 10 |
| NCERT exemplar for class 12 maths Chapter 6 | NCERT exemplar for class 12 maths Chapter 11 |
latest video
news via inbox
Nulla turp dis cursus. Integer liberos euismod pretium faucibua











