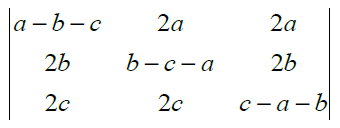NCERT Exemplar for Class 12 Maths Chapter 4 Determinants

NCERT Exemplar for Class 12 Maths is an effective way to grasp the in-depth knowledge of the chapter and its related concepts. Students will be able to solve as many possible questions and get a better hold through regular practice of these exemplars. Through the provided step wise solutions, they will comprehend better and perform incredibly well in their 12th board examinations.

NCERT exemplar for Class 12 Maths Chapter 4 Determinants contains a total of 29 important questions. Students can easily access them by scrolling below and practising them consistently to score maximum marks. Our subject matter experts at SimplyAcad have put their best to assist students in learning difficult and complex concepts for their effective learning. Along with this, there are several NCERT exemplar for class 12 maths of all the chapters provided on this platform.

Access Solutions of the NCERT Exemplar Class 12 Maths Chapter 4 Determinants

Using the properties of determinants in Exercises 1 to 6, evaluate:

1.

Solution:

= (x2 – 2x + 2) . (x + 1) – (x – 1) . 0

= x3 – 2×2 + 2x + x2 – 2x + 2

= x3 – x2 + 2

2.

Solution:

3.

Solution:

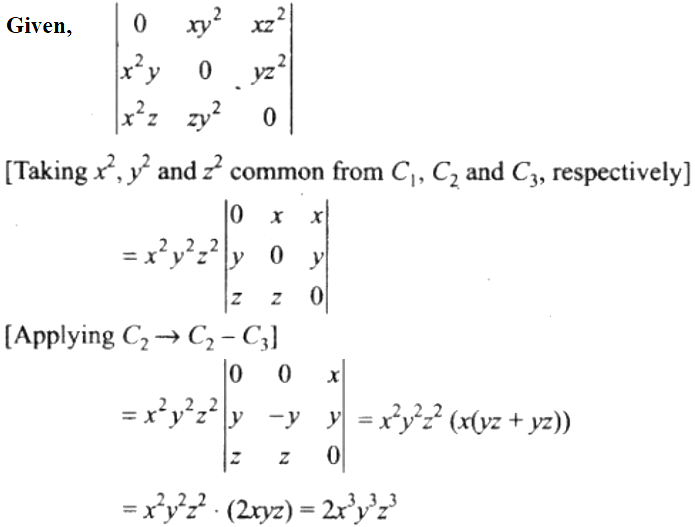
4.

Solution:

[Expanding along first column]

= (x + y + z) . 1[3y(3z + x) + (3z)(x – y)]

= (x + y + z)(3yz + 3yx + 3xz)

= 3(x + y + z)(xy + yz + zx)

5.

Solution:

6.

Solution:

Lastly, expanding along R1, we have

= (a + b + c) [1 x 0 + (a + b + c)2]

= (a + b + c)3

Using the properties of determinants in Exercises 7 to 9, prove that:

7.

Solution:

8.

Solution:

9.

Solution:

 

12. Find the value of q satisfying

Solution:

13. If , then find values of x.

Solution:

14. If a1, a2, a3, …, ar are in G.P., then prove that the determinant

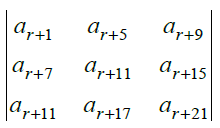
is independent of r.

Solution:

Hence, the determinant is independent of r.

 

17. Find A–1 if and show that A-1 = (A2 – 3I)/ 2.

Solution:

Long Answer (L.A.)

18. If A = , find A-1.

Using A–1, solve the system of linear equations

x – 2y = 10 , 2x – y – z = 8 , –2y + z = 7.

Solution:

 

20.Solve the system of equations:

{y+2z=7x−y=32x+3y+4z=17\begin{cases} y + 2z = 7 \\ x – y = 3 \\ 2x + 3y + 4z = 17 \end{cases}⎩⎨⎧​y+2z=7x−y=32x+3y+4z=17​

Solution

Solve for zzz from the first equation:

y+2z=7  ⟹  z=7−y2y + 2z = 7 \implies z = \frac{7 – y}{2}y+2z=7⟹z=27−y​

Solve for xxx from the second equation:

x−y=3  ⟹  x=y+3x – y = 3 \implies x = y + 3x−y=3⟹x=y+3

Substitute xxx and zzz into the third equation and solve for yyy:

2(y+3)+3y+2(7−y)=172(y + 3) + 3y + 2(7 – y) = 172(y+3)+3y+2(7−y)=17 3y+20=17  ⟹  y=−13y + 20 = 17 \implies y = -13y+20=17⟹y=−1

Find xxx and zzz:

x=−1+3=2,z=7−(−1)2=4x = -1 + 3 = 2, \quad z = \frac{7 – (-1)}{2} = 4x=−1+3=2,z=27−(−1)​=4

Solution:

x=2,y=−1,z=4x = 2, \quad y = -1, \quad z = 4x=2,y=−1,z=4

21.Given that a+b+c≠0a + b + c \neq 0a+b+c=0 and

Δ=∣abcbcacab∣=0\Delta = \left| \begin{array}{ccc} a & b & c \\ b & c & a \\ c & a & b \end{array} \right| = 0Δ=​abc​bca​cab​​=0

we need to prove that a=b=ca = b = ca=b=c using properties of determinants.

Solution:

Perform Column Operation: Apply the operation C1→C1+C2+C3C_1 \to C_1 + C_2 + C_3C1​→C1​+C2​+C3​:
Δ=∣a+b+cbca+b+ccaa+b+cab∣\Delta = \left| \begin{array}{ccc} a + b + c & b & c \\ a + b + c & c & a \\ a + b + c & a & b \end{array} \right|Δ=​a+b+ca+b+ca+b+c​bca​cab​​

Factor Out (a+b+c)(a + b + c)(a+b+c):
Δ=(a+b+c)∣1bc1ca1ab∣\Delta = (a + b + c) \left| \begin{array}{ccc} 1 & b & c \\ 1 & c & a \\ 1 & a & b \end{array} \right|Δ=(a+b+c)​111​bca​cab​​

Simplify Using Row Operations:
Perform row operations R2→R2−R1R_2 \to R_2 – R_1R2​→R2​−R1​ and R3→R3−R1R_3 \to R_3 – R_1R3​→R3​−R1​:
Δ=(a+b+c)∣1bc0c−ba−c0a−bb−c∣\Delta = (a + b + c) \left| \begin{array}{ccc} 1 & b & c \\ 0 & c – b & a – c \\ 0 & a – b & b – c \end{array} \right|Δ=(a+b+c)​100​bc−ba−b​ca−cb−c​​

Expand the Determinant:
Expand along the first column:
Δ=(a+b+c)[(c−b)(b−c)−(a−c)(a−b)]\Delta = (a + b + c) \left[ (c – b)(b – c) – (a – c)(a – b) \right]Δ=(a+b+c)[(c−b)(b−c)−(a−c)(a−b)]

Simplify the Expression:
Simplify the expression inside the brackets:
(c−b)(b−c)=−(c−b)2,(a−c)(a−b)=a2−a(b+c)+bc(c – b)(b – c) = -(c – b)^2, \quad (a – c)(a – b) = a^2 – a(b + c) + bc(c−b)(b−c)=−(c−b)2,(a−c)(a−b)=a2−a(b+c)+bc Δ=(a+b+c)[−(c−b)2−(a2−a(b+c)+bc)]\Delta = (a + b + c) \left[ -(c – b)^2 – (a^2 – a(b + c) + bc) \right]Δ=(a+b+c)[−(c−b)2−(a2−a(b+c)+bc)] Δ=−12(a+b+c)[(a−b)2+(b−c)2+(c−a)2]\Delta = -\frac{1}{2} (a + b + c) \left[ (a – b)^2 + (b – c)^2 + (c – a)^2 \right]Δ=−21​(a+b+c)[(a−b)2+(b−c)2+(c−a)2]

Conclude:
Given that Δ=0\Delta = 0Δ=0 and a+b+c≠0a + b + c \neq 0a+b+c=0, we have:
(a−b)2+(b−c)2+(c−a)2=0(a – b)^2 + (b – c)^2 + (c – a)^2 = 0(a−b)2+(b−c)2+(c−a)2=0
This implies:
a=b,b=c,c=aa = b, \quad b = c, \quad c = aa=b,b=c,c=a
Therefore, a=b=ca = b = ca=b=c.

Hence, proved.

 

22. Prove that is divisible by a + b + c and find the quotient.

Solution:

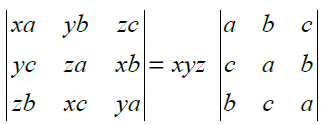
23. If x + y + z = 0, prove that

Solution:

Objective Type Questions (M.C.Q.)

Choose the correct answer from given four options in each of the Exercises from 24 to 37.

24. If then, value of x is

(A) 3 (B) ± 3 (C) ± 6 (D) 6

Solution:

Option (C) ± 6

From the given,

On equating the determinants, we have

2×2 – 40 = 18 + 14

2×2 = 72

x2 = 36

Thus, x = ± 6

25. The value of determinant

(A) a3 + b3 + c3 (B) 3 bc (C) a3 + b3 + c3 – 3abc (D) none of these

Solution:

Option (C) a3 + b3 + c3 – 3abc

26. The area of a triangle with vertices (–3, 0), (3, 0) and (0, k) is 9 sq. units. The value of k will be

(A) 9 (B) 3 (C) – 9 (D) 6

Solution: Option (B) 3

27. The determinant equals

(A) abc (b–c) (c – a) (a – b) (B) (b–c) (c – a) (a – b)

(C) (a + b + c) (b – c) (c – a) (a – b) (D) None of these

Solution: Option (D)

28. The number of distinct real roots of = 0 in the interval -π/4 ≤ x ≤ π/4 is

(A) 0 (B) 2 (C) 1 (D) 3

Solution: Option (C) 1

29. If A, B and C are angles of a triangle, then the determinant is equal to

(A) 0 (B) -1 (C) 1 (D) None of these

Solution: Option (A) 0

NCERT Exemplar For Class 12 Maths

The NCERT exemplars are an effective study material for scoring higher marks in the examination paper. Students must practise these additional questions for their own benefits, as these are curated by the best subject-matter experts to boost both knowledge and confidence. Students can easily access the ncert exemplar for class 12 maths by visiting our website SimplyAcad and solve all the questions listed to secure maximum marks.

Here are some other NCERT exemplar for class 12 maths:

NCERT exemplar for class 12 maths Chapter 1	NCERT exemplar for class 12 maths Chapter 7
NCERT exemplar for class 12 maths Chapter 2	NCERT exemplar for class 12 maths Chapter 8
NCERT exemplar for class 12 maths Chapter 3	NCERT exemplar for class 12 maths Chapter 9
NCERT exemplar for class 12 maths Chapter 5	NCERT exemplar for class 12 maths Chapter 10
NCERT exemplar for class 12 maths Chapter 6	NCERT exemplar for class 12 maths Chapter 11