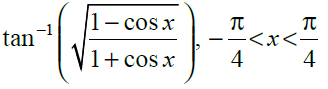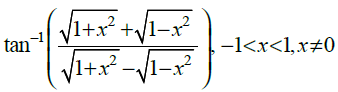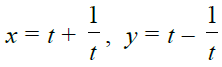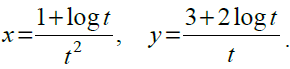NCERT Exemplar Class 12 Maths Chapter 5 Continuity And Differentiability
NCERT Exemplar for Class 12 Maths Chapter 5
Students who are looking for study materials to learn the mathematical concepts thoroughly must refer to the NCERT Exemplar for Class 12 Maths to grasp the in-depth knowledge of the chapters. Through the provided solutions, students can comprehend the concepts in a better way which raises their confidence. They will be able to solve as many possible questions and get a better hold of the concept through regular practices and revisions. The step wise solutions allow them to observe, analyse and learn each step of the answer which is a must for students preparing for their upcoming 12th board examinations.
NCERT exemplar for Class 12 Maths Chapter 5 Continuity And Differentiability contains a total of 53 important questions. Students can easily access them by scrolling below and practise them consistently to score maximum marks. Our subject matter experts at SimplyAcad have put their best to assist students in learning difficult and complex concepts for their effective learning. Along with this, there are several NCERT exemplar for class 12 maths of all the chapters provided on this platform.
Access Solutions of the NCERT Exemplar Chapter 5 Continuity And Differentiability
1. Find if the function given below is continuous or discontinuous at the indicated point: \[ f(x) = \begin{cases} x + 5, & \text{if } x \geq 2 \\ x^2, & \text{if } x < 2 \end{cases} \] at \( x = 2 \). \section*
{Solution} To determine the continuity of \( f(x) \) at \( x = 2 \), we need to check if the right-hand limit, the left-hand limit, and the function value at \( x = 2 \) are equal. \subsection*{Right-Hand Limit} \[ \text{RHL} = \lim_{x \to 2^+} f(x) \] Given: \[ f(x) = x + 5 \text{ for } x \geq 2 \] So, \[ \text{RHL} = \lim_{x \to 2^+} (2 + 5) = 7 \] \subsection*{Left-Hand Limit} \[ \text{LHL} = \lim_{x \to 2^-} f(x) \] Given: \[ f(x) = x^2 \text{ for } x < 2 \] So, \[ \text{LHL} = \lim_{x \to 2^-} (2^2) = 4 \] \subsection*{Function Value} \[ f(2) = 2 + 5 = 7 \] \subsection*{Conclusion} Since: \[ \text{LHL} \neq \text{RHL} \] The limit does not exist at \( x = 2 \). Thus, the function \( f(x) \) is discontinuous at \( x = 2 \).
2.
 at x = 0
at x = 0
Solution:
Checking the right hand and left hand limits of the given function, we have

Therefore, the given function f(x) is discontinuous at x = 0.
4.
 at x = 2
at x = 2
Solution:


Thus, f(x) is continuous at x = 2.
5.
 at x = 4
at x = 4
Solution:
Checking the right hand and left hand limits for the given function, we have
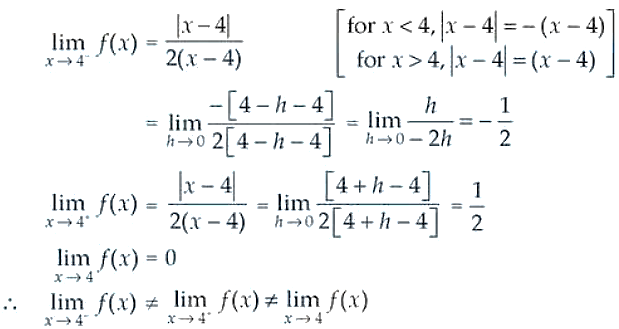
Thus, f(x) is discontinuous at x = 4.
6.
 at x = 0
at x = 0
Solution:
Checking the right hand and left hand limits for the given function, we have


Thus, the given function f(x) is continuous at x = 0.
7.
 at x = a
at x = a
Solution:
Checking the right hand and left hand limits for the given function, we have
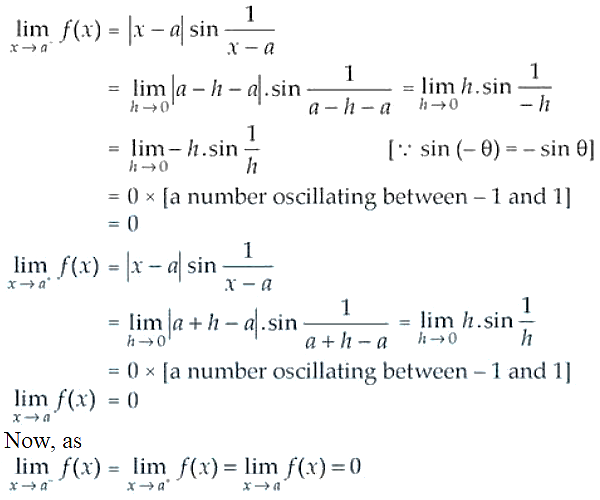
Thus, the given function f(x) is continuous at x = 0.
8.
 at x = 0
at x = 0
Solution:
Checking the right hand and left hand limits for the given function, we have

Thus, f(x) is discontinuous at x = 0.
9.
 at x = 1
at x = 1
Solution:
Checking the right hand and left hand limits for the given function, we have

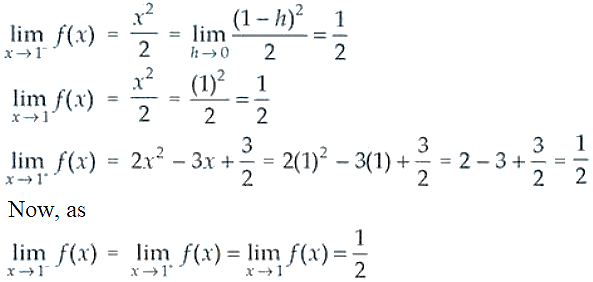
Thus, the given function f(x) is continuous at x = 1.
10. f (x) = |x| + |x – 1| at x = 1
Solution:
Checking the right hand and left hand limits for the given function, we have

Thus, f(x) is continuous at x = 1.
Find the value of k in each of the Exercises 11 to 14 so that the function f is continuous at the indicated point:
11.

Solution:
Finding the left hand and right hand limits for the given function, we have
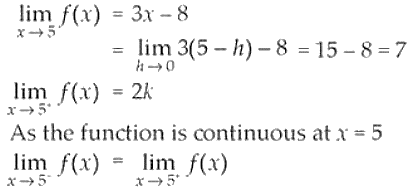
So,
7 = 2k
k = 7/2 = 3.5
Therefore, the value of k is 3.5
12.

Solution:
The given function f(x) can be rewritten as,

So, k = ½
Therefore, the value of k is ½
13.

Solution:
Finding the left hand and right hand limits for the given function, we have


Therefore, the value of k is -1
14.

Solution:
Finding the left hand and right hand limits for the given function, we have


Therefore, the value of k is ± 1
15. Prove that the function \( f \) defined by \[ f(x) = \begin{cases} x |x| + 2x^2, & \text{if } x \neq 0 \\ k, & \text{if } x = 0 \end{cases} \] remains discontinuous at \( x = 0 \) regardless of the choice of \( k \). \section*
{Solution} To prove that the function \( f(x) \) is discontinuous at \( x = 0 \) regardless of the value of \( k \), we will examine the left-hand limit (LHL), right-hand limit (RHL), and the value of the function at \( x = 0 \) and compare them. Given: \[ f(x) = \begin{cases} x |x| + 2x^2, & \text{if } x \neq 0 \\ k, & \text{if } x = 0 \end{cases} \] We need to find the limits and function value at \( x = 0 \). \subsection*{Left-Hand Limit} \[ \text{LHL} = \lim_{x \to 0^-} f(x) \] For \( x < 0 \), \( |x| = -x \), so: \[ f(x) = x(-x) + 2x^2 = -x^2 + 2x^2 = x^2 \] Thus: \[ \text{LHL} = \lim_{x \to 0^-} x^2 = 0 \] \subsection*{Right-Hand Limit} \[ \text{RHL} = \lim_{x \to 0^+} f(x) \] For \( x > 0 \), \( |x| = x \), so: \[ f(x) = x(x) + 2x^2 = x^2 + 2x^2 = 3x^2 \] Thus: \[ \text{RHL} = \lim_{x \to 0^+} 3x^2 = 0 \] \subsection*{Function Value} \[ f(0) = k \] \subsection*{Conclusion} Since: \[ \text{LHL} = \text{RHL} = 0 \] and: \[ f(0) = k \] \[ \text{LHL} \neq f(0) \text{ for any } k \neq 0 \] Thus, the function \( f(x) \) is discontinuous at \( x = 0 \) regardless of the choice of \( k \).
16. Find the values of a and b such that the function f defined by

is a continuous function at x = 4.
Solution:
Finding the left hand and right hand limit for the given function, we have

So, -1 + a = a + b = 1 + b
-1 + a = a + b and 1 + b = a + b
We get, b = -1 and 1 + -1 = a + -1 ⇒ a = 1
Therefore, the value of a = 1 and b = -1
17. Given \( f(x) = \frac{1}{x – 1} \). Find the point(s) of discontinuity of the composite function \( y = f(f(x)) \). \section*
{Solution} To find the points of discontinuity of the composite function \( y = f(f(x)) \), follow these steps: 1. **Determine \( f(f(x)) \)**: Compute \( f(f(x)) \): \[ f(x) = \frac{1}{x – 1} \] Substitute \( f(x) \) into \( f \): \[ f(f(x)) = f\left(\frac{1}{x – 1}\right) \] Since \( f(x) = \frac{1}{x – 1} \), replace \( x \) with \( \frac{1}{x – 1} \): \[ f\left(\frac{1}{x – 1}\right) = \frac{1}{\frac{1}{x – 1} – 1} \] Simplify the denominator: \[ \frac{1}{\frac{1 – (x – 1)}{x – 1}} = \frac{1}{\frac{2 – x}{x – 1}} \] Therefore: \[ f(f(x)) = \frac{x – 1}{2 – x} \] 2. **Find where \( f(f(x)) \) is undefined**: The function \( f(f(x)) \) is undefined where the denominator is zero: \[ 2 – x = 0 \implies x = 2 \] Thus, \( f(f(x)) \) is undefined at \( x = 2 \). 3. **Determine the points of discontinuity**: Since \( f(f(x)) \) is not defined at \( x = 2 \), the function is discontinuous at \( x = 2 \). \textbf{Summary:} The composite function \( y = f(f(x)) = \frac{x – 1}{2 – x} \) is discontinuous at \( x = 2 \) because it is not defined at this point.
18. Find all points of discontinuity of the function
Solution:

Now,
if f(t) is discontinuous, then 2 – x = 0 ⇒ x = 2
And, 2x – 1 = 0 ⇒ x = ½
Therefore, the required points of discontinuity for the given function are 2 and ½.
19. Show that the function f (x) = |sin x + cos x| is continuous at x = p. Examine the differentiability of f, where f is defined by
Solution:
Given,
f(x) = |sin x + cos x| at x = π
Now, put g(x) = sin x + cos x and h(x) = |x|
Hence, h[g(x)] = h(sin x + cos x) = |sin x + cos x|
Now,
g(x) = sin x + cos x is a continuous function since sin x and cos x are two continuous functions at x = π.
We know that, every modulus function is a common function is a continuous function everywhere.
Therefore, f(x) = |sin x + cos x| is continuous function at x = π.
20.
 at x = 2.
at x = 2.
Solution:
We know that, a function f is differentiable at a point ‘a’ in its domain if
Lf’(c) = Rf’(c)

Therefore, f(x) is not differentiable at x = 2.

21.
Solution:
Given,


Therefore, f(x) is differentiable at x = 0

22.
Solution:
We know that, f(x) is differentiable at x = 2 if

Thus, f(x) is not differentiable at x = 2.
Differentiate each of the following w.r.t. x (Exercises 25 to 43) :
25. 
Solution:

26.

Solution:
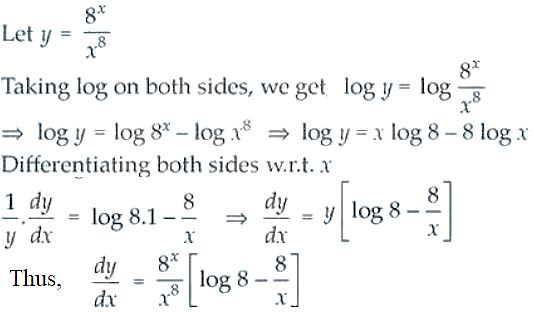
27. 
Solution:

28.

Solution:


29.

Solution:
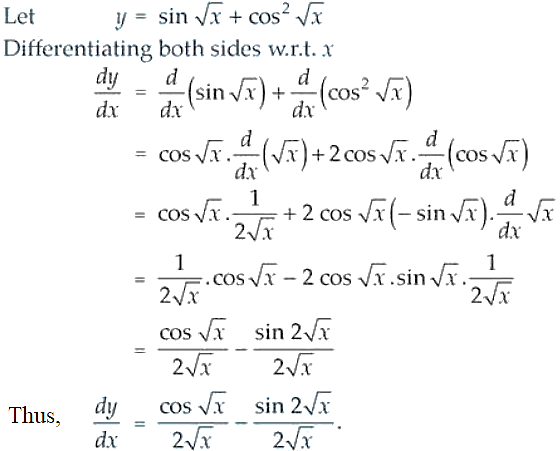
30. sinn (ax2 + bx + c)
Solution:

31.

Solution:

32. sin x2 + sin2 x + sin2 (x2)
Solution:

33.
Solution:

34. (sin x)cos x
Solution:


35. sinm x . cosn x
Solution:

36. (x + 1)2 + (x + 2)3 + (x + 3)4
Solution:


37.

Solution:
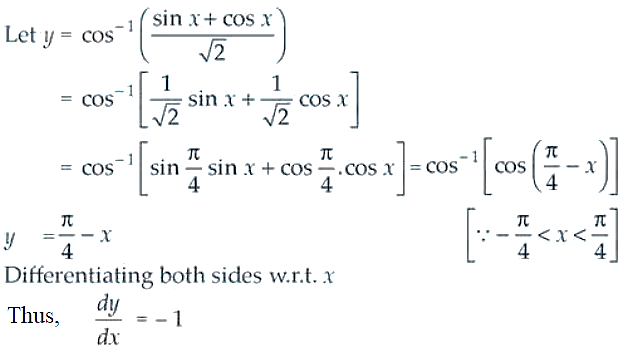
38.

Solution:


39.

Solution:

40.

Solution:

41.

Solution:


42.

Solution:

43.

Solution:

Find dy/dx of each of the functions expressed in parametric form in Exercises from 44 to 48.
44.

Solution:
Given,
x = t + 1/t, y = t – 1/t
Differentiating both the parametric functions w.r.t θ

45.

Solution:
Given,
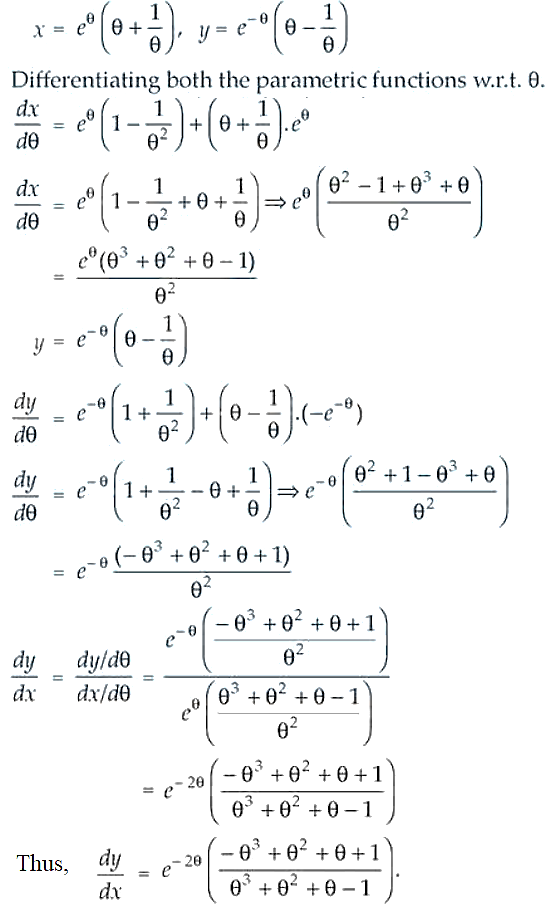

46. x = 3cosq – 2cos3q, y = 3sinq – 2sin3q.
Solution:
Given, x = 3cosq – 2cos3q, y = 3sinq – 2sin3q.
Differentiating both the parametric functions w.r.t. q

47.

Solution:
Given,
sin x = 2t/(1 + t2), tan y = 2t/ (1 – t2)
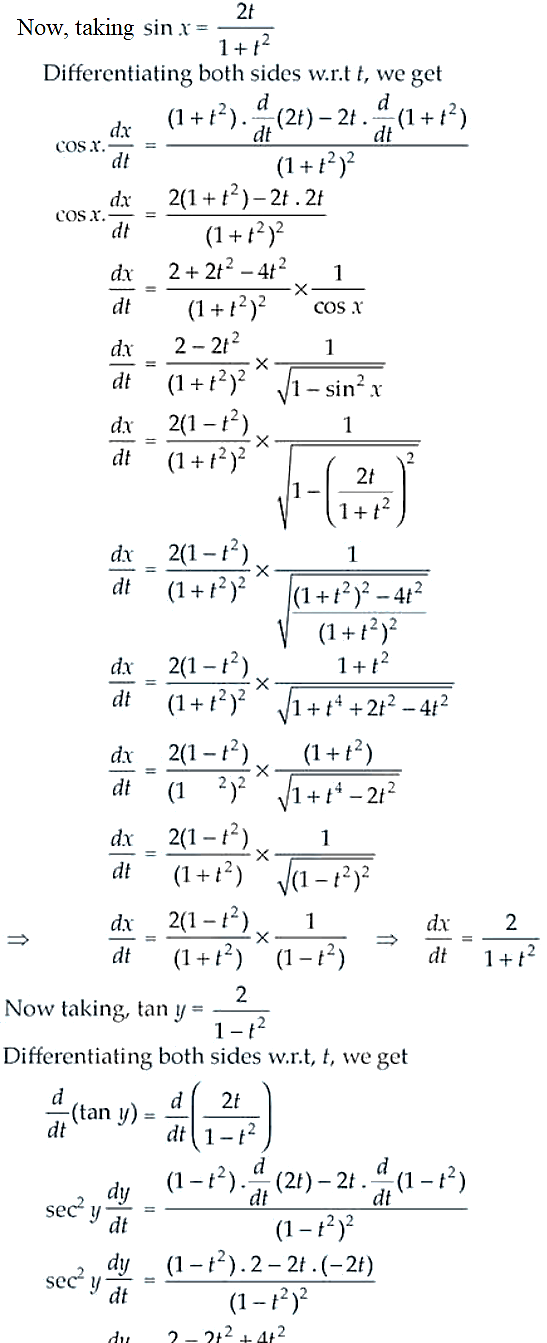
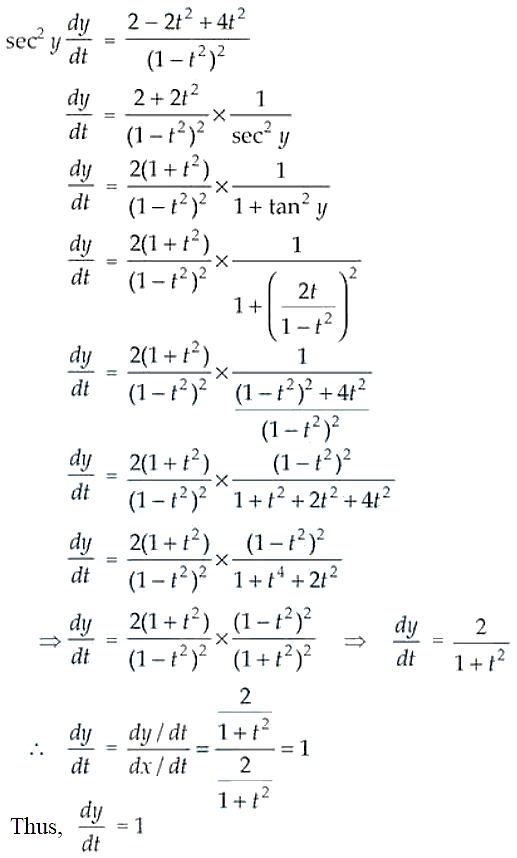
48.

Solution:
On differentiating both the given parametric functions w.r.t. t, we have


49. If x = ecos2t and y = esin2t, prove that dy/ dx = – y log x/ x log y.
Solution:
Given,
x = ecos2t and y = esin2t
So, cos 2t = log x and sin 2t = log y
Now, differentiating both the parameter functions w.r.t t, we have

51.If \[ x = 3 \sin t \] and \[ y = 3 \cos t, \] then find \[ \frac{dy}{dx} \] at \[ t = \frac{\pi}{3}. \] \section*
{Solution} We have: \[ x = 3 \sin t \] Differentiating with respect to \( t \), we get: \[ \frac{dx}{dt} = 3 \cos t. \] Similarly, \[ y = 3 \cos t \] Differentiating with respect to \( t \), we get: \[ \frac{dy}{dt} = -3 \sin t. \] Thus, \[ \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{-3 \sin t}{3 \cos t} = -\tan t. \] At \( t = \frac{\pi}{3} \): \[ \frac{dy}{dx} = -\tan \left(\frac{\pi}{3}\right). \] \[ \tan \left(\frac{\pi}{3}\right) = \sqrt{3}. \] \[ \frac{dy}{dx} = -\sqrt{3}. \] \end{document}
52. Differentiate x/sinx w.r.t sin x.
Solution:


NCERT Exemplar For Class 12 Maths
The NCERT exemplars are an effective study material for scoring higher marks in the examination paper. Students must practise these additional questions for their own benefits, as these are curated by the best subject-matter experts to boost both knowledge and confidence. Students can easily access the ncert exemplar for class 12 maths by visiting our website SimplyAcad and solve all the questions listed to secure maximum marks.
Here are some other NCERT exemplar for class 12 maths:
| NCERT exemplar for class 12 maths Chapter 1 | NCERT exemplar for class 12 maths Chapter 7 |
|---|---|
| NCERT exemplar for class 12 maths Chapter 2 | NCERT exemplar for class 12 maths Chapter 8 |
| NCERT exemplar for class 12 maths Chapter 3 | NCERT exemplar for class 12 maths Chapter 9 |
| NCERT exemplar for class 12 maths Chapter 4 | NCERT exemplar for class 12 maths Chapter 10 |
| NCERT exemplar for class 12 maths Chapter 6 | NCERT exemplar for class 12 maths Chapter 11 |
latest video
news via inbox
Nulla turp dis cursus. Integer liberos euismod pretium faucibua

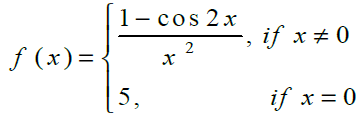 at x = 0
at x = 0 at x = 2
at x = 2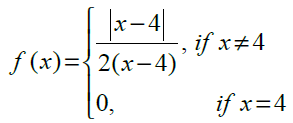 at x = 4
at x = 4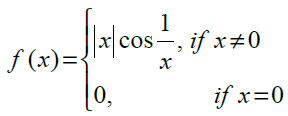 at x = 0
at x = 0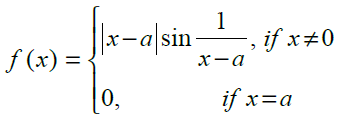 at x = a
at x = a at x = 0
at x = 0 at x = 1
at x = 1



 at x = 2.
at x = 2.