NCERT Exemplar for Class 12 Maths Chapter 9: Differential Equations

Students must refer to the NCERT Exemplar for Class 12 Maths which is an effective way to learn and get deep insights of the concepts discussed in the mathematics chapters. This will ensure that learners can solve as many possible questions and get a better hold through regular practice of these exemplars. Our subject experts at SimplyAcad have made sure to assist students thoroughly by providing detailed stepwise solutions which will benefit the students a lot in their board exams. The Solutions for the NCERT exemplar for Class 12 Maths Chapter 9 Differential Equations are provided below which contains a total of 33 important questions of short and long type. Students can easily access them by scrolling below and practise them consistently to score maximum marks. Along with this, there are several NCERT exemplar for class 12 maths of all the chapters provided on this platform.

Access Solutions of the NCERT Exemplar Class 12 Maths Differential Equations: Short Answer Questions

1. Find the solution of

Solution:

 

2. Find the differential equation of all non-vertical lines in a plane.

Solution:

We know that, the equation of all non-vertical lines are y = mx + c

On differentiating w.r.t. x, we get

dy/dx = m

Again, on differentiating w.r.t. x, we have

d2y/dx2 = 0

Thus, the required equation is d2y/dx2 = 0.

 

3. Given that \( \frac{dy}{dx} = e^{-2y} \) and \( y = 0 \) when \( x = 5 \), find the value of \( x \) when \( y = 3 \). \textbf

{Solution:} Given, \[ \frac{dy}{dx} = e^{-2y} \] Rearranging, \[ \frac{dy}{e^{-2y}} = dx \] \[ e^{2y} \, dy = dx \] Integrating both sides, \[ \int e^{2y} \, dy = \int dx \] \[ \frac{e^{2y}}{2} = x + C \] where \( C \) is the constant of integration. Given that \( y = 0 \) when \( x = 5 \), we can find \( C \) using this condition: \[ \frac{e^{2 \cdot 0}}{2} = 5 + C \] \[ \frac{1}{2} = 5 + C \] \[ C = \frac{1}{2} – 5 = -\frac{9}{2} \] Substituting \( C \) back into the equation, \[ \frac{e^{2y}}{2} = x – \frac{9}{2} \] Solving for \( x \) when \( y = 3 \), \[ \frac{e^{2 \cdot 3}}{2} = x – \frac{9}{2} \] \[ \frac{e^6}{2} = x – \frac{9}{2} \] \[ x = \frac{9}{2} + \frac{e^6}{2} \] \[ x = \frac{1}{2} (9 + e^6) \] Hence, the required value of \( x \) when \( y = 3 \) is \( \frac{1}{2} (9 + e^6) \).

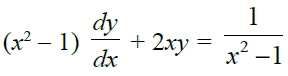
4. Solve the differential equation

Solution:

5. Solve the differential equation

Solution:

Given differential equation,

dy/dx + 2xy = y

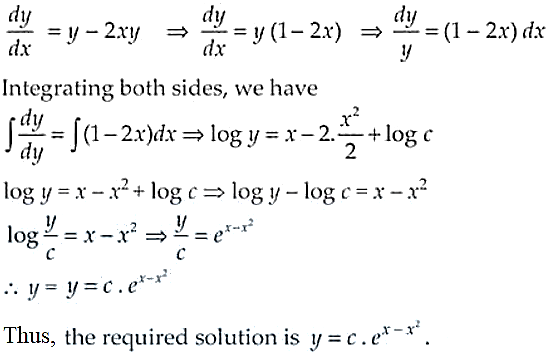
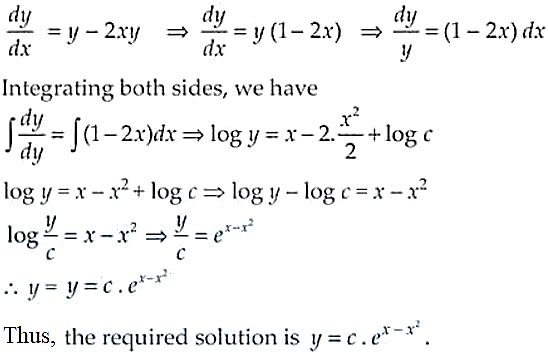
6. Find the general solution of

Solution:

Given equation, dy/dx + ay = emx

Solving for linear differential equation of first order, we have

P = a and Q = emx

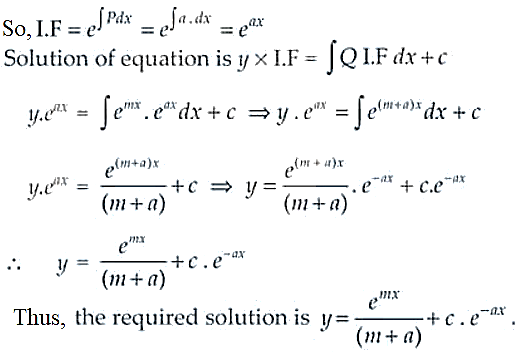
7. Solve the differential equation

Solution:

Given differential equation, dy/dx + 1 = ex+y

Substituting x + y = t and differentiating w.r.t. x, we have

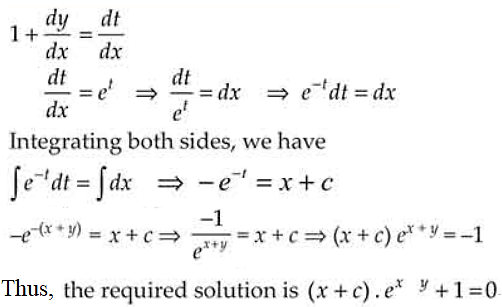
8. Solve the differential equation: \[ y \, dx – x \, dy = x^2 y \, dx \] \textbf

{Solution:} Given: \[ y \, dx – x \, dy = x^2 y \, dx \] Rearrange to: \[ y \, dx – x \, dy – x^2 y \, dx = 0 \] \[ y \, dx – x^2 y \, dx = x \, dy \] \[ (y – x^2 y) \, dx = x \, dy \] \[ \frac{dy}{dx} = \frac{y – x^2 y}{x} \] \[ \frac{dy}{dx} = \frac{y(1 – x^2)}{x} \] \[ \frac{dy}{dx} + \frac{x – 1}{x} y = 0 \] This is a linear differential equation of the form: \[ \frac{dy}{dx} + P(x) y = Q(x) \] where: \[ P(x) = \frac{x – 1}{x}, \quad Q(x) = 0 \] The integrating factor \( I_F \) is given by: \[ I_F = e^{\int P(x) \, dx} \] \[ I_F = e^{\int \frac{x – 1}{x} \, dx} \] \[ I_F = e^{\int \left(1 – \frac{1}{x}\right) \, dx} \] \[ I_F = e^{x – \log x} \] \[ I_F = e^x \cdot e^{-\log x} \] \[ I_F = \frac{e^x}{x} \] The general solution is: \[ y \cdot \frac{e^x}{x} = \int 0 \cdot \frac{e^x}{x} \, dx + C \] \[ y \cdot \frac{e^x}{x} = C \] \[ y = C \cdot \frac{x}{e^x} \] \[ y = C \cdot x \cdot e^{-x} \] Hence, the general solution to the differential equation is: \[ y = C \cdot x \cdot e^{-\frac{x^2}{2}} \]

9. Solve the differential equation: \[ \frac{dy}{dx} = 1 + x + y^2 + xy^2 \] with the initial condition \( y = 0 \) when \( x = 0 \). \textbf

{Solution:} Given: \[ \frac{dy}{dx} = 1 + x + y^2 + xy^2 \] Rearrange and factor: \[ \frac{dy}{dx} = (1 + x) + y^2 (1 + x) \] \[ \frac{dy}{dx} = (1 + x)(1 + y^2) \] Separate the variables: \[ \frac{dy}{1 + y^2} = (1 + x) \, dx \] Integrate both sides: \[ \int \frac{dy}{1 + y^2} = \int (1 + x) \, dx \] \[ \tan^{-1}(y) = x + \frac{x^2}{2} + C \] Apply the initial condition \( y = 0 \) when \( x = 0 \): \[ \tan^{-1}(0) = 0 + \frac{0^2}{2} + C \] \[ 0 = C \] So: \[ \tan^{-1}(y) = x + \frac{x^2}{2} \] Solving for \( y \): \[ y = \tan \left( x + \frac{x^2}{2} \right) \] Hence, the required solution is: \[ y = \tan \left( x + \frac{x^2}{2} \right) \]

10. Find the general solution of (x + 2y3) dy/dx = y.

Solution:

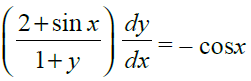
11. Let \( y = y(x) \) be a solution curve of the differential equation: \[ (y + 1) \tan^2 x \, dx + \tan x \, dy + y \, dx = 0, \quad x \in \left(0, \frac{\pi}{2}\right) \] If \[ \lim_{x \to 0^+} x y(x) = 1 \] then find the value of \( y\left(\frac{\pi}{4}\right) \). \textbf

{Solution:} The given differential equation is: \[ (y + 1) \tan^2 x \, dx + \tan x \, dy + y \, dx = 0 \] Rewrite the differential equation: \[ (y + 1) (\sec^2 x – 1) \, dx + \tan x \, d(y + 1) + y \, dx = 0 \] Simplify: \[ (y + 1) \sec^2 x \, dx + \tan x \, d(y + 1) – (y + 1) \, dx + y \, dx = 0 \] \[ (y + 1) \, d(\tan x) + \tan x \, d(y + 1) = dx \] Integrate both sides: \[ \int d \left[ (y + 1) \tan x \right] = \int dx \] \[ (y + 1) \tan x = x + C \] Solve for \( y \): \[ y = \frac{x + C}{\tan x} – 1 \] Apply the initial condition \( \lim_{x \to 0^+} x y(x) = 1 \): \[ \lim_{x \to 0^+} x \left( \frac{x + C}{\tan x} – 1 \right) = 1 \] Use the approximation \( \tan x \approx x \) for small \( x \): \[ \lim_{x \to 0^+} x \left( \frac{x + C}{x} – 1 \right) = 1 \] \[ \lim_{x \to 0^+} (x + C – x) = 1 \] \[ C = 1 \] So the solution is: \[ y = \frac{x + 1}{\tan x} – 1 \] To find \( y\left(\frac{\pi}{4}\right) \): \[ y\left(\frac{\pi}{4}\right) = \frac{\frac{\pi}{4} + 1}{\tan\left(\frac{\pi}{4}\right)} – 1 \] \[ \tan\left(\frac{\pi}{4}\right) = 1 \] \[ y\left(\frac{\pi}{4}\right) = \frac{\frac{\pi}{4} + 1}{1} – 1 \] \[ y\left(\frac{\pi}{4}\right) = \frac{\pi}{4} + 1 – 1 \] \[ y\left(\frac{\pi}{4}\right) = \frac{\pi}{4} \] Therefore, the required value is \( \frac{\pi}{4} \).

12. If \( y(t) \) is a solution of \[ (1 + t) \frac{dy}{dt} – t y = 1 \] and \( y(0) = -1 \), then show that \( y(1) = -\frac{1}{2} \). \textbf

{Solution:} Given: \[ (1 + t) \frac{dy}{dt} – t y = 1 \] Rewrite this in the standard linear differential equation form: \[ \frac{dy}{dt} – \frac{t}{1 + t} y = \frac{1}{1 + t} \] Comparing with the standard linear differential equation \[ \frac{dy}{dt} + P(t) y = Q(t), \] we identify: \[ P(t) = -\frac{t}{1 + t}, \quad Q(t) = \frac{1}{1 + t} \] To solve this, we need the integrating factor (I.F.): \[ \text{I.F.} = e^{\int P(t) \, dt} \] Calculate \( \int P(t) \, dt \): \[ \int -\frac{t}{1 + t} \, dt \] Substitute \( u = 1 + t \), thus \( du = dt \): \[ \int -\frac{t}{1 + t} \, dt = \int -\frac{u – 1}{u} \, du = \int -1 + \frac{1}{u} \, du \] \[ = -u + \log |u| + C = -(1 + t) + \log |1 + t| + C \] Thus, \[ \text{I.F.} = e^{-(1 + t) + \log |1 + t|} = e^{-(1 + t)} \cdot |1 + t| \] Since \(1 + t > 0\), we simplify to: \[ \text{I.F.} = \frac{1 + t}{e^{1 + t}} \] Multiply both sides of the differential equation by the integrating factor: \[ \frac{1 + t}{e^{1 + t}} \cdot \left[ (1 + t) \frac{dy}{dt} – t y \right] = \frac{1 + t}{e^{1 + t}} \cdot \frac{1}{1 + t} \] \[ \frac{d}{dt} \left[ y \cdot \frac{1 + t}{e^{1 + t}} \right] = \frac{1}{e^{1 + t}} \] Integrate both sides with respect to \( t \): \[ y \cdot \frac{1 + t}{e^{1 + t}} = \int \frac{1}{e^{1 + t}} \, dt + C \] \[ y \cdot \frac{1 + t}{e^{1 + t}} = -e^{-(1 + t)} + C \] \[ y = \frac{-e^{-(1 + t)} + C}{\frac{1 + t}{e^{1 + t}}} = -\frac{1}{1 + t} + C e^{1 + t} \] Using the initial condition \( y(0) = -1 \): \[ -1 = -\frac{1}{1 + 0} + C e^{1 + 0} \] \[ -1 = -1 + C e \] \[ C e = 0 \quad \text{thus,} \quad C = 0 \] So the solution simplifies to: \[ y = -\frac{1}{1 + t} \] Evaluate \( y \) at \( t = 1 \): \[ y(1) = -\frac{1}{1 + 1} = -\frac{1}{2} \] Hence, the required value is: \[ y(1) = -\frac{1}{2} \]

13. Form the differential equation having y = (sin–1x)2 + A cos–1x + B, where A and B are arbitrary constants, as its general solution.

Solution:

14. Form the differential equation of all circles which pass through the origin and whose centres lie on the \( y \)-axis. \textbf

{Solution:} Let \((0, k)\) be the center of the circle and \(k\) be the radius. The equation of the circle is: \[ (x – 0)^2 + (y – k)^2 = k^2 \] Simplify this equation: \[ x^2 + (y – k)^2 = k^2 \] \[ x^2 + y^2 – 2ky = k^2 \] Rearrange the equation: \[ x^2 + y^2 – 2ky = 0 \] To find the differential equation, differentiate this equation with respect to \( x \): \[ 2x + 2y \frac{dy}{dx} – 2k \frac{dy}{dx} = 0 \] \[ 2x + 2y \frac{dy}{dx} – 2k \frac{dy}{dx} = 0 \] \[ 2x + 2(y – k) \frac{dy}{dx} = 0 \] Rearrange this to isolate \( \frac{dy}{dx} \): \[ 2(y – k) \frac{dy}{dx} = -2x \] \[ \frac{dy}{dx} = \frac{-x}{y – k} \] Substitute \( k = \frac{x^2 + y^2}{2y} \) from \( k = \frac{x^2 + y^2}{2y} \): \[ \frac{dy}{dx} = \frac{-x}{y – \frac{x^2 + y^2}{2y}} \] Combine the terms: \[ \frac{dy}{dx} = \frac{-x}{\frac{2y^2 – x^2 – y^2}{2y}} \] \[ \frac{dy}{dx} = \frac{-2xy}{y^2 – x^2} \] Rearrange to get the final differential equation: \[ (y^2 – x^2) \frac{dy}{dx} + 2xy = 0 \] Thus, the required differential equation of the circles that pass through the origin and whose centers lie on the \( y \)-axis is: \[ (x^2 – y^2) \frac{dy}{dx} + 2xy = 0 \]

15. Find the equation of a curve passing through the origin and satisfying the differential equation \[ (1 + x^2) \frac{dy}{dx} + 2xy = 4x^2 \] \textbf

{Solution:} Given: \[ (1 + x^2) \frac{dy}{dx} + 2xy = 4x^2 \] Rearrange it: \[ \frac{dy}{dx} + \frac{2x}{1 + x^2} y = \frac{4x^2}{1 + x^2} \] This is a linear differential equation of the form: \[ \frac{dy}{dx} + P(x) y = Q(x) \] where \[ P(x) = \frac{2x}{1 + x^2} \] \[ Q(x) = \frac{4x^2}{1 + x^2} \] To solve this, we need the integrating factor \( I.F. \). It is given by: \[ I.F. = e^{\int P(x) \, dx} \] Substitute \( P(x) \): \[ I.F. = e^{\int \frac{2x}{1 + x^2} \, dx} \] Let \( t = 1 + x^2 \), hence \( dt = 2x \, dx \): \[ I.F. = e^{\int \frac{1}{t} \, dt} \] \[ I.F. = e^{\ln |t|} = |t| = 1 + x^2 \] So, the integrating factor is: \[ I.F. = 1 + x^2 \] The general solution is: \[ y \cdot I.F. = \int Q(x) \cdot I.F. \, dx + C \] Substitute \( I.F. \) and \( Q(x) \): \[ y \cdot (1 + x^2) = \int \frac{4x^2}{1 + x^2} \cdot (1 + x^2) \, dx + C \] \[ y \cdot (1 + x^2) = \int 4x^2 \, dx + C \] \[ y \cdot (1 + x^2) = \frac{4x^3}{3} + C \] As the curve passes through the origin \((0, 0)\), we have: \[ 0 \cdot (1 + 0^2) = \frac{4 \cdot 0^3}{3} + C \] \[ C = 0 \] Thus, the equation of the curve is: \[ y = \frac{4x^3}{3(1 + x^2)} \]

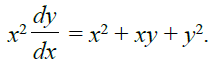
16. Solve:

Solution:

Given equation,

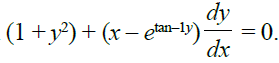
17.Find the general solution of the differential equation \[ \frac{dy}{dx} + \frac{1 – y^2}{1 – x^2} = 0 \] \textbf

{Solution:} Given differential equation: \[ \frac{dy}{dx} + \frac{1 – y^2}{1 – x^2} = 0 \] Rearrange to isolate \(\frac{dy}{dx}\): \[ \frac{dy}{dx} = -\frac{1 – y^2}{1 – x^2} \] Rewriting this in separable form: \[ \frac{dy}{1 – y^2} = -\frac{dx}{1 – x^2} \] Integrate both sides: \[ \int \frac{dy}{1 – y^2} = -\int \frac{dx}{1 – x^2} \] Recall the integral formulas: \[ \int \frac{dy}{1 – y^2} = \frac{1}{2} \ln \left| \frac{1 + y}{1 – y} \right| + C_1 \] \[ \int \frac{dx}{1 – x^2} = \frac{1}{2} \ln \left| \frac{1 + x}{1 – x} \right| + C_2 \] Thus, we have: \[ \frac{1}{2} \ln \left| \frac{1 + y}{1 – y} \right| = -\frac{1}{2} \ln \left| \frac{1 + x}{1 – x} \right| + C \] Combining the constants: \[ \ln \left| \frac{1 + y}{1 – y} \right| = – \ln \left| \frac{1 + x}{1 – x} \right| + C’ \] Exponentiating both sides: \[ \frac{1 + y}{1 – y} = e^{C’} \cdot \frac{1 – x}{1 + x} \] Letting \( e^{C’} = k \), we get: \[ \frac{1 + y}{1 – y} = k \cdot \frac{1 – x}{1 + x} \] Solving for \(k\), we get the general solution: \[ \sin^{-1} x + \sin^{-1} y = C \] where \( C \) is the constant of integration. .

18. Find the general solution of the differential equation \[ y^2 \, dx + (x^2 – xy + y^2) \, dy = 0 \] \textbf

{Solution:} Rewrite the differential equation: \[ y^2 \, dx + (x^2 – xy + y^2) \, dy = 0 \] Rearrange to isolate \(\frac{dy}{dx}\): \[ \frac{dy}{dx} = -\frac{y^2}{x^2 – xy + y^2} \] Let \( \frac{y}{x} = v \), so \( y = vx \). Then: \[ \frac{dy}{dx} = v + x \frac{dv}{dx} \] Substitute into the differential equation: \[ v + x \frac{dv}{dx} = -\frac{(vx)^2}{x^2 – vx \cdot x + (vx)^2} \] Simplify the denominator: \[ x^2 – vx \cdot x + (vx)^2 = x^2 – vx^2 + v^2 x^2 = x^2 (1 – v + v^2) \] Thus: \[ \frac{dy}{dx} = -\frac{v^2 x^2}{x^2 (1 – v + v^2)} = -\frac{v^2}{1 – v + v^2} \] Substitute into the equation: \[ v + x \frac{dv}{dx} = -\frac{v^2}{1 – v + v^2} \] Rearrange: \[ x \frac{dv}{dx} = -\frac{v^2}{1 – v + v^2} – v \] \[ x \frac{dv}{dx} = -\frac{v^2 + v(1 – v + v^2)}{1 – v + v^2} \] \[ x \frac{dv}{dx} = -\frac{v^2 + v – v^2 + v^3}{1 – v + v^2} \] \[ x \frac{dv}{dx} = -\frac{v^3 + v}{1 – v + v^2} \] Separate variables and integrate: \[ -\frac{dx}{x} = \frac{(1 – v + v^2)}{v(1 + v^2)} \, dv \] Integrate both sides: \[ -\ln x = \int \frac{1 – v + v^2}{v(1 + v^2)} \, dv \] \[ -\ln x = -\tan^{-1} v + \ln v + C \] Combining the constants: \[ \ln v + \ln x – \tan^{-1} v = C \] \[ \ln(vx) – \tan^{-1} v = C \] By substituting \( v = \frac{y}{x} \): \[ \ln \left(\frac{y}{x} x \right) – \tan^{-1} \left(\frac{y}{x}\right) = C \] \[ \ln y – \tan^{-1} \left(\frac{y}{x}\right) = C \] Therefore, the general solution is: \[ \ln y – \tan^{-1} \left(\frac{y}{x}\right) = C \]

19. Solve the differential equation: \[ (x + y) \left( dx – dy \right) = dx + dy \] \textbf

{Solution:} Rewrite the given differential equation: \[ (x + y) \left( dx – dy \right) = dx + dy \] Expanding and rearranging: \[ (x + y) dx – (x + y) dy = dx + dy \] \[ (x + y) dx – dx = (x + y) dy + dy \] \[ (x + y – 1) dx = (x + y + 1) dy \] Separate the variables: \[ \frac{dx}{x + y + 1} = \frac{dy}{x + y – 1} \] Integrate both sides: \[ \int \frac{dx}{x + y + 1} = \int \frac{dy}{x + y – 1} \] After integration: \[ \log |x + y + 1| = x – y + C \] where \(C\) is the constant of integration. Therefore, the solution to the differential equation is: \[ \log |x + y + 1| = x – y + C \]

20. Solve the differential equation: \[ 2(y + 3) – x y \frac{dy}{dx} = 0 \] given that \( y(1) = -2 \). \section*

{Solution} Given: \[ 2(y + 3) – x y \frac{dy}{dx} = 0 \] Rearrange to solve for \(\frac{dy}{dx}\): \[ x y \frac{dy}{dx} = 2(y + 3) \] \[ \frac{dy}{dx} = \frac{2(y + 3)}{x y} \] Separate the variables: \[ \frac{y}{y + 3} \, dy = \frac{2}{x} \, dx \] Integrate both sides: \[ \int \frac{y}{y + 3} \, dy = \int \frac{2}{x} \, dx \] To integrate the left side, use substitution: Let \( u = y + 3 \), hence \( du = dy \). So: \[ \int \frac{y}{y + 3} \, dy = \int \frac{u – 3}{u} \, du = \int \left(1 – \frac{3}{u}\right) \, du \] \[ = \int du – 3 \int \frac{1}{u} \, du \] \[ = u – 3 \ln |u| + C_1 \] Substitute back \( u = y + 3 \): \[ \int \frac{y}{y + 3} \, dy = (y + 3) – 3 \ln |y + 3| + C_1 \] Integrate the right side: \[ \int \frac{2}{x} \, dx = 2 \ln |x| + C_2 \] Combine the results: \[ (y + 3) – 3 \ln |y + 3| = 2 \ln |x| + C \] where \( C = C_2 – C_1 \) is the constant of integration. Use the initial condition \( y(1) = -2 \): \[ (-2 + 3) – 3 \ln |-2 + 3| = 2 \ln |1| + C \] \[ 1 – 3 \ln |1| = C \] \[ C = 1 \] Thus, the general solution is: \[ (y + 3) – 3 \ln |y + 3| = 2 \ln |x| + 1 \] Rearrange: \[ (y + 3) = 3 \ln |y + 3| + 2 \ln |x| + 1 \] Exponentiate to solve explicitly: \[ e^{(y + 3)} = e^{3 \ln |y + 3| + 2 \ln |x| + 1} \] \[ e^{(y + 3)} = (y + 3)^3 x^2 e \] Therefore, the required solution is: \[ (y + 3)^3 x^2 = e^{y + 2} \]

21. Solve the differential equation \[ \frac{dy}{dx} = \cos x \left( 2 – y \csc x \right) \] given that \( y = 2 \) when \( x = \frac{\pi}{2} \). \section*

{Solution} Given: \[ \frac{dy}{dx} = \cos x \left( 2 – y \csc x \right) \] Rearrange the equation: \[ \frac{dy}{dx} = 2 \cos x – y \cos x \cdot \csc x \] \[ \frac{dy}{dx} = 2 \cos x – y \cot x \] \[ \frac{dy}{dx} + y \cot x = 2 \cos x \] This is a linear differential equation of the form: \[ \frac{dy}{dx} + P(x) y = Q(x) \] where \( P(x) = \cot x \) and \( Q(x) = 2 \cos x \). The integrating factor (I.F.) is given by: \[ \text{I.F.} = e^{\int \cot x \, dx} \] \[ = e^{\ln |\sin x|} \] \[ = |\sin x| \] Multiplying the differential equation by the integrating factor: \[ y \cdot |\sin x| = \int 2 \cos x \cdot |\sin x| \, dx + C \] \[ y \cdot \sin x = \int 2 \cos x \sin x \, dx + C \] Using the identity \( \sin 2x = 2 \sin x \cos x \), we get: \[ y \sin x = \frac{1}{2} \int \sin 2x \, dx + C \] \[ y \sin x = -\frac{1}{2} \cos 2x + C \] Substituting the initial condition \( y = 2 \) when \( x = \frac{\pi}{2} \): \[ 2 \cdot \sin \frac{\pi}{2} = -\frac{1}{2} \cos 2 \cdot \frac{\pi}{2} + C \] \[ 2 = -\frac{1}{2} (-1) + C \] \[ 2 = \frac{1}{2} + C \] \[ C = \frac{3}{2} \] Therefore, the solution to the differential equation is: \[ y \sin x = -\frac{1}{2} \cos 2x + \frac{3}{2} \]

22. Form the differential equation by eliminating \(A\) and \(B\) in \(Ax^2 + By^2 = 1\). \section*

{Solution} Given: \[ Ax^2 + By^2 = 1 \] Differentiating with respect to \(x\), we get: \[ 2Ax + 2By \frac{dy}{dx} = 0 \] \[ Ax + By \frac{dy}{dx} = 0 \] \[ \frac{A}{B} + \frac{y}{x} \frac{dy}{dx} = 0 \] Differentiating again with respect to \(x\): \[ \frac{d}{dx}\left(\frac{A}{B}\right) + \frac{d}{dx}\left(\frac{y}{x} \frac{dy}{dx}\right) = 0 \] This gives: \[ \frac{y}{x} \frac{d^2 y}{dx^2} + \left(\frac{x \frac{dy}{dx} – y}{x^2}\right) \frac{dy}{dx} = 0 \] \[ x y \frac{d^2 y}{dx^2} + \left(x \frac{dy}{dx} – y\right) \frac{dy}{dx} = 0 \] Simplifying, we obtain the required differential equation: \[ x y \frac{d^2 y}{dx^2} + x \left(\frac{dy}{dx}\right)^2 – y \frac{dy}{dx} = 0 \]

23. Solve the differential equation \((1 + y^2) \tan^{-1} x \, dx + 2y(1 + x^2) \, dy = 0\). \section*

{Solution} Given: \[ (1 + y^2) \tan^{-1} x \, dx + 2y(1 + x^2) \, dy = 0 \] \[ \Rightarrow 2y(1 + x^2) \, dy = -(1 + y^2) \tan^{-1} x \, dx \] \[ \Rightarrow \frac{2y}{1 + y^2} \, dy = -\frac{\tan^{-1} x}{1 + x^2} \, dx \] Integrating both sides: \[ \int \frac{2y}{1 + y^2} \, dy = -\int \frac{\tan^{-1} x}{1 + x^2} \, dx \] Let \( 1 + y^2 = t \) and \( \tan^{-1} x = z \), so: \[ 2y \, dy = dt \quad \text{and} \quad \frac{1}{1 + x^2} dx = dz \] Thus, the integral becomes: \[ \int \frac{1}{t} \, dt = -\int z \, dz \] \[ \Rightarrow \ln |t| = -\frac{z^2}{2} + C \] \[ \Rightarrow \ln |1 + y^2| = -\frac{(\tan^{-1} x)^2}{2} + C \] \[ \Rightarrow \ln |1 + y^2| + \frac{(\tan^{-1} x)^2}{2} = C \] Hence, the required solution is: \[ \ln |1 + y^2| + \frac{(\tan^{-1} x)^2}{2} = C \]

24. Find the differential equation of system of concentric circles with centre (1, 2).

Solution:

The family of concentric circles with centre (1, 2) and radius ‘r’ is given by

(x – 1)2 + (y – 2)2 = r2

Differentiating both sides w.r.t, x we get

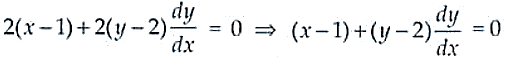
Thus, the above is the required equation.

Access Solutions of the NCERT Exemplar Class 12 Maths Differential Equations – Long Answer Questions

 

25. Solve :

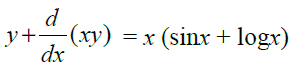
Solution:

Given differential equation,

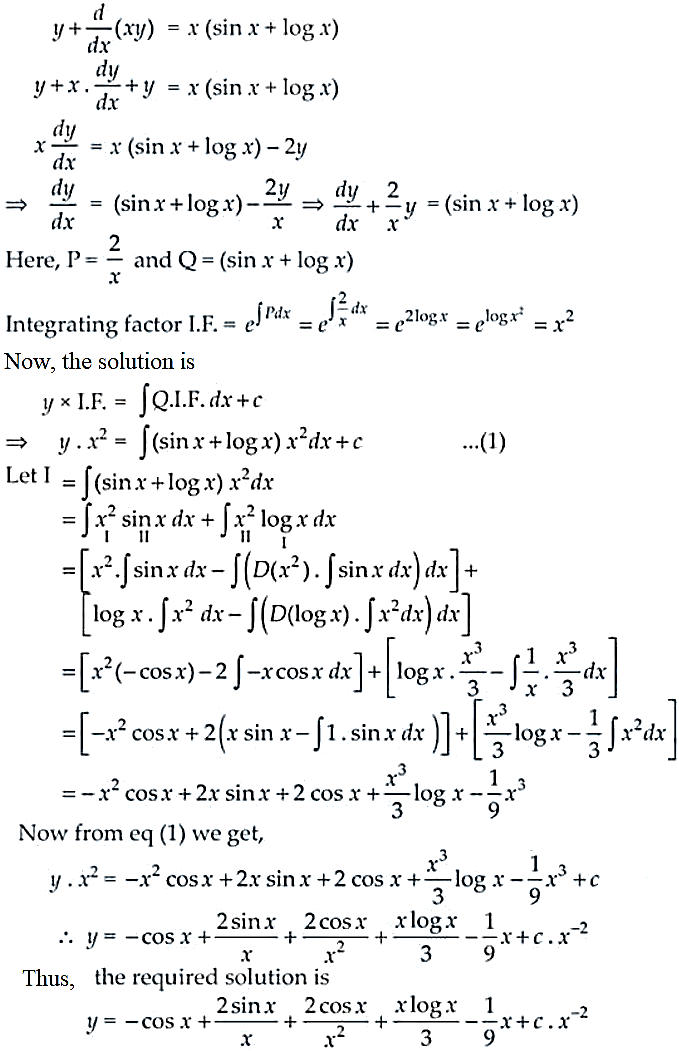
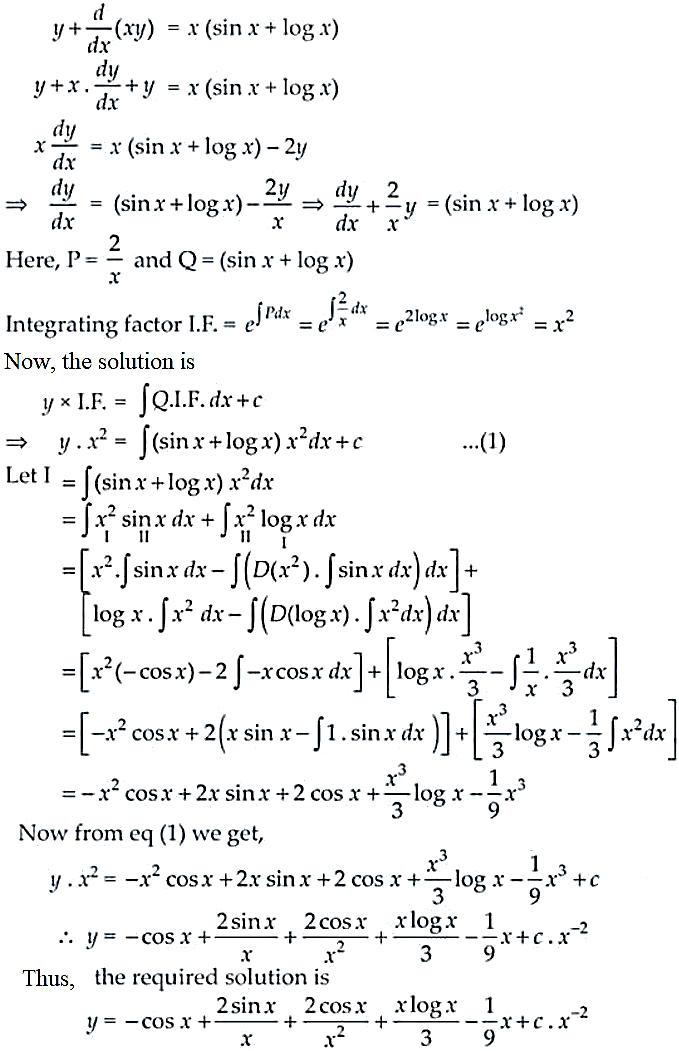
26. Find the general solution of \[ (1 + \tan y)(dx – dy) + 2x \, dy = 0 \] \section*

{Solution} Given: \[ (1 + \tan y)(dx – dy) + 2x \, dy = 0 \] \[ \Rightarrow (1 + \tan y)(dx – dy) = 2x \, dy \] \[ \Rightarrow \frac{dx}{dy} – 1 = -\frac{2x}{1 + \tan y} \] \[ \Rightarrow \frac{dx}{dy} + \frac{2x}{1 + \tan y} = 1 \] This is a linear differential equation of the form: \[ \frac{dx}{dy} + xP(y) = Q(y) \] Here, \( P(y) = \frac{2}{1 + \tan y} \) and \( Q(y) = 1 \). The integrating factor (I.F.) is given by: \[ \text{I.F.} = e^{\int P(y) \, dy} = e^{\int \frac{2}{1 + \tan y} \, dy} \] \[ = e^{\int \frac{2 \, dy}{\cos y + \sin y}} \] Using the substitution \( \sin y + \cos y = t \), we get: \[ d(\sin y + \cos y) = (\cos y – \sin y) \, dy = dt \] Thus, the integral becomes: \[ \int \frac{1}{t} \, dt = \ln |t| = \ln |\sin y + \cos y| \] Therefore, the integrating factor is: \[ \text{I.F.} = e^{y + \ln |\sin y + \cos y|} = e^y |\sin y + \cos y| \] The solution to the differential equation is given by: \[ x \cdot \text{I.F.} = \int (\text{I.F.}) \cdot Q(y) \, dy + C \] \[ \Rightarrow x \cdot e^y |\sin y + \cos y| = \int e^y |\sin y + \cos y| \, dy + C \] \[ \Rightarrow x \cdot e^y (\sin y + \cos y) = \int e^y (\sin y + \cos y) \, dy + k \] \[ \Rightarrow x \cdot e^y (\sin y + \cos y) = e^y \sin y + k \] Thus, the required solution is: \[ x (\sin y + \cos y) = \sin y + k e^{-y} \]

27. Solve the differential equation: \[ \frac{dy}{dx} = \cos(x + y) + \sin(x + y) \] \section*

{Solution} We start with the given differential equation: \[ \frac{dy}{dx} = \sin(x + y) + \cos(x + y) \] Let \( x + y = v \), so that \( \frac{dy}{dx} = \frac{dv}{dx} – 1 \). Substituting this into the equation, we get: \[ \frac{dv}{dx} – 1 = \sin v + \cos v \] Rearranging, we have: \[ \frac{dv}{dx} = 1 + \sin v + \cos v \] Now, separating the variables: \[ \frac{dv}{1 + \sin v + \cos v} = dx \] To solve the integral on the left, we simplify using the identity: \[ 1 + \sin v + \cos v = \left(1 + \frac{\sin v + \cos v}{\sqrt{2}}\right)\sqrt{2} \] Thus, we rewrite the integral as: \[ \int \frac{dv}{\left(1 + \frac{\sin v + \cos v}{\sqrt{2}}\right)\sqrt{2}} = \int dx \] We simplify further by noticing that \( \sin v + \cos v = \sqrt{2} \sin\left(v + \frac{\pi}{4}\right) \): \[ \frac{dv}{1 + \sqrt{2}\sin\left(v + \frac{\pi}{4}\right)} = dx \] Integrating both sides, we get: \[ \ln\left(1 + \tan\left(\frac{v}{2}\right)\right) = x + C \] Substituting back \( v = x + y \), we obtain: \[ \ln\left(1 + \tan\left(\frac{x + y}{2}\right)\right) = x + C \] This is the general solution to the differential equation.

28. Find the general solution of dy/dx – 3y = sin 2x.

Solution:

Given equation, dy/dx – 3y = sin 2x

It’s a first order linear differential equation

Here P = -3 and Q = sin 2x

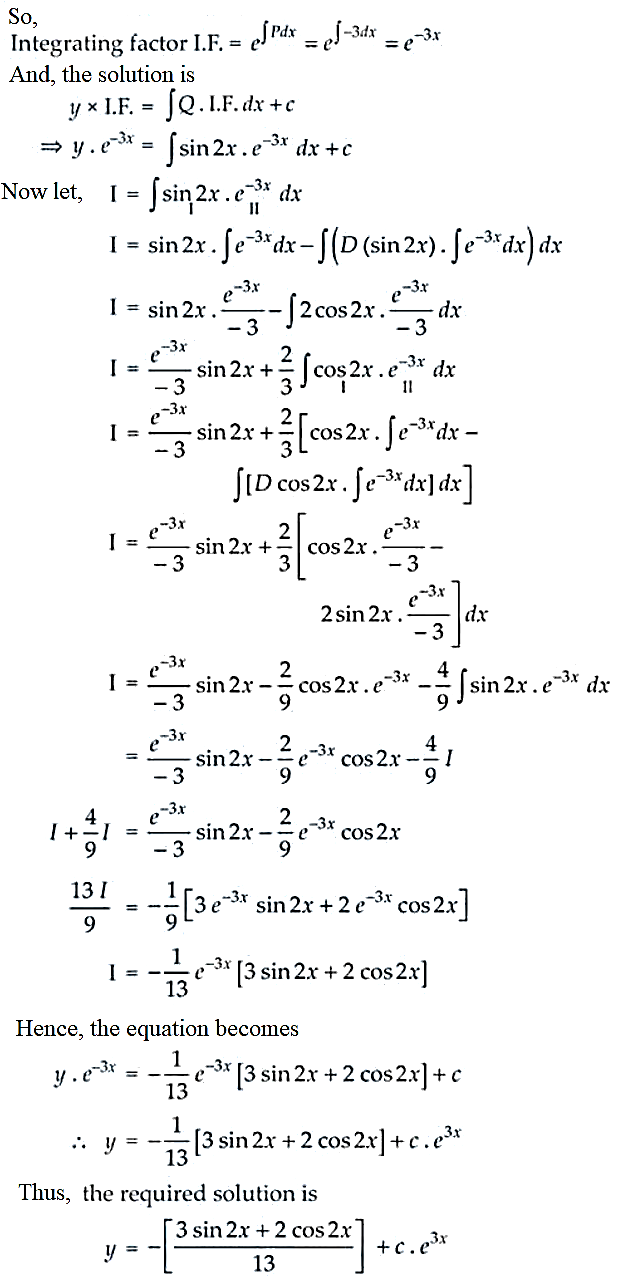
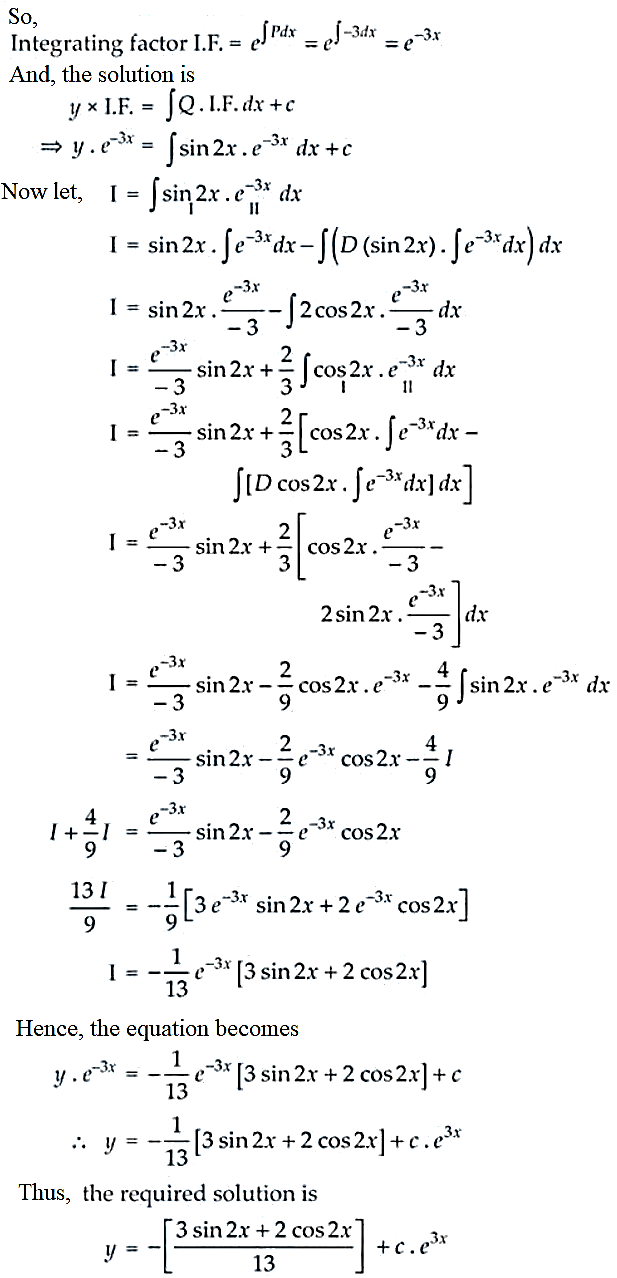
29. Find the equation of a curve passing through \((2, 1)\) if the slope of the tangent to the curve at any point \((x, y)\) is \(\frac{x^2 + y^2}{2xy}\). \section*

{Solution} Given: The slope of the tangent at point \((x, y)\) is \[ \frac{dy}{dx} = \frac{x^2 + y^2}{2xy} \] This can be rewritten as: \[ \frac{dy}{dx} = \frac{1}{2} \left[\frac{x}{y} + \frac{y}{x}\right] \] Let \(y = vx\), so that: \[ \frac{dy}{dx} = v + x\frac{dv}{dx} \] Substituting into the differential equation: \[ v + x\frac{dv}{dx} = \frac{1}{2} \left[\frac{1}{v} + v\right] \] This simplifies to: \[ x\frac{dv}{dx} = \frac{1}{2} \left[\frac{1}{v} – v\right] = \frac{1 – v^2}{2v} \] Separating the variables: \[ 2v \frac{1 – v^2}{dv} = \frac{dx}{x} \] Integrating both sides: \[ \int \frac{2v}{1 – v^2} dv = \int \frac{dx}{x} \] Let \(1 – v^2 = t\), then \(-2v dv = dt\), so: \[ -\int \frac{1}{t} dt = \ln|x| + c \] This simplifies to: \[ -\ln|t| = \ln|x| + c \] or \[ \ln|t| + \ln|x| = -c \] which simplifies further to: \[ \ln|tx| = -c \] Thus: \[ |tx| = e^{-c} = k \] Substituting back \(t = 1 – v^2\): \[ (1 – v^2)x = k \] And since \(v = \frac{y}{x}\): \[ (1 – \frac{y^2}{x^2})x = k \] Given that the curve passes through \((2, 1)\), substituting: \[ (1 – \frac{1^2}{2^2})2 = k \] This gives: \[ k = \frac{3}{2} \] Hence, the equation of the curve is: \[ (1 – \frac{y^2}{x^2})x = \frac{3}{2} \] Or simplifying: \[ 2(x^2 – y^2) = 3x \]

30. Find the equation of the curve through the point \((1, 0)\). If the slope of the tangent to the curve at any point \((x, y)\) is \(\frac{y – 1}{x^2 + x}\). \section*

{Solution} Given that the slope of the tangent to the curve at any point \((x, y)\) is \(\frac{y – 1}{x^2 + x}\). Since the slope of the tangent to the curve is \(\frac{dy}{dx}\), we have: \[ \frac{dy}{dx} = \frac{y – 1}{x^2 + x} \] Separating the variables, we get: \[ \frac{dy}{y – 1} = \frac{dx}{x(x + 1)} \] Now, resolving \(\frac{1}{x(x + 1)}\) into partial fractions: \[ \frac{1}{x(x + 1)} = \frac{A}{x} + \frac{B}{x + 1} \] So, \[ 1 = A(x + 1) + Bx \] Equating the coefficients of like terms: \[ \text{For } x: \quad 0 = A + B \] \[ \text{For constant term: } \quad 1 = A \] This gives \(A = 1\) and \(B = -1\). Thus: \[ \frac{1}{x(x + 1)} = \frac{1}{x} – \frac{1}{x + 1} \] Substituting this back: \[ \frac{dy}{y – 1} = \left(\frac{dx}{x} – \frac{dx}{x + 1}\right) \] Integrating both sides, we get: \[ \int \frac{dy}{y – 1} = \int \frac{dx}{x} – \int \frac{dx}{x + 1} \] \[ \log(y – 1) = \log x – \log(x + 1) + \log C \] Simplifying: \[ \log(y – 1) = \log\left(\frac{Cx}{x + 1}\right) \] Taking the exponential on both sides: \[ y – 1 = \frac{Cx}{x + 1} \] Thus: \[ (y – 1)(x + 1) = Cx \] Substituting the given point \((1, 0)\) to find \(C\): \[ (0 – 1)(1 + 1) = C(1) \] \[ -2 = C \] Therefore, the equation of the curve is: \[ (y – 1)(x + 1) = -2x \] or equivalently: \[ (y – 1)(x + 1) + 2x = 0 \] Hence, the required equation of the curve through the point \((1, 0)\) is: \[ (y – 1)(x + 1) + 2x = 0 \]

31. Find the equation of the curve passing through the point \((0, 1)\), if the slope of the tangent to the curve at each of its points is equal to the sum of the abscissa and the product of the abscissa and ordinate of the point. \section*

{Solution} According to the question, the slope of the tangent to the curve is given by: \[ \frac{dy}{dx} = x + xy \] This can be rewritten as: \[ \frac{dy}{dx} – xy = x \] Comparing this with the standard form of the linear differential equation: \[ \frac{dy}{dx} + Py = Q \] we have \(P = -x\) and \(Q = x\). The integrating factor (I.F.) is given by: \[ \text{I.F.} = e^{-\int P dx} = e^{-\int (-x) dx} = e^{\frac{x^2}{2}} \] Multiplying the differential equation by the integrating factor, we get: \[ y \cdot e^{\frac{x^2}{2}} = \int x \cdot e^{\frac{x^2}{2}} dx + C \] Letting \( -\frac{x^2}{2} = t \), we have: \[ dt = -x dx \] Thus, the integral becomes: \[ -\int e^t dt = -e^t + C \] Substituting back: \[ y \cdot e^{\frac{x^2}{2}} = -e^{-\frac{x^2}{2}} + C \] Since the curve passes through the point \((0, 1)\), we substitute \(x = 0\) and \(y = 1\) into the equation: \[ 1 \cdot e^0 = -e^0 + C \] \[ 1 = -1 + C \Rightarrow C = 2 \] Therefore, the equation of the curve is: \[ y \cdot e^{\frac{x^2}{2}} = -e^{-\frac{x^2}{2}} + 2 \] Simplifying, we get: \[ y = -1 + 2e^{-\frac{x^2}{2}} \] Hence, the required equation of the curve is: \[ y = -1 + 2e^{-\frac{x^2}{2}} \]

32. A curve \( C \) has the property that if the tangent drawn at any point \( P \) on \( C \) meets the coordinate axes at \( A \) and \( B \), and \( P \) is the midpoint of \( AB \). If the curve passes through the point \( (1,1) \), then what is the equation of the curve? \section*

{Solution} Given that the point \( P(x, y) \) on the curve \( C \) is the midpoint of the line segment \( AB \), where \( A \) and \( B \) are the points where the tangent at \( P \) intersects the coordinate axes. Let the equation of the tangent at \( P(x, y) \) be: \[ \frac{x}{a} + \frac{y}{b} = 1 \] where \( A = (a, 0) \) and \( B = (0, b) \). Since \( P \) is the midpoint of \( AB \), we have: \[ \left( \frac{a}{2}, \frac{b}{2} \right) = (x, y) \] This gives: \[ a = 2x \quad \text{and} \quad b = 2y \] Substituting these values into the tangent equation, we get: \[ \frac{x}{2x} + \frac{y}{2y} = 1 \] Simplifying, we find: \[ \frac{1}{2} + \frac{1}{2} = 1 \] This equation is always true, indicating that the curve has the property described. Given that the curve passes through the point \( (1,1) \), we substitute \( x = 1 \) and \( y = 1 \) into the general equation \( xy = k \) to find \( k \): \[ 1 \cdot 1 = k \Rightarrow k = 1 \] Thus, the equation of the curve is: \[ xy = 1 \] Therefore, the correct equation of the curve is: \[ \boxed{xy = 1} \]

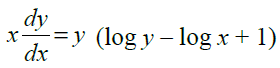
33. Solve :

Solution:

 

Additional NCERT Exemplars for Class 12 Maths:

The NCERT exemplars are an effective study material for scoring higher marks in the examination paper. Students must practise these additional questions for their own benefits, as these are curated by the best subject-matter experts to boost both knowledge and confidence. Students can easily access the ncert exemplar for class 12 maths by visiting our website SimplyAcad and solve all the questions listed to secure maximum marks.

Here are some other NCERT exemplar for class 12 maths:

NCERT exemplar for class 12 maths Chapter 1	NCERT exemplar for class 12 maths Chapter 6
NCERT exemplar for class 12 maths Chapter 2	NCERT exemplar for class 12 maths Chapter 7
NCERT exemplar for class 12 maths Chapter 3	NCERT exemplar for class 12 maths Chapter 8
NCERT exemplar for class 12 maths Chapter 4	NCERT exemplar for class 12 maths Chapter 10
NCERT exemplar for class 12 maths Chapter 5	NCERT exemplar for class 12 maths Chapter 11