NCERT Exemplar for Class 12 Physics Chapter 2

NCERT Exemplar for Class 12 Physics will help students to deepen their knowledge related to the topic of Electrostatic Potential and Capacitance. This provided exemplar by SimplyAcad allows students to cover all the areas and sections comprising the chapter 2 of the Physics textbook. Students can easily access this NCERT exemplar for class 12 Physics in this article below to perform incredibly well in their upcoming 12th board examinations.

NCERT exemplar for Class 12 Physics Chapter 2 contains a total of 33 questions in distinct patterns including MCQs of two different types, very short, short and long answers type questions. Apart from these there are several NCERT exemplar for class 12 science of all the chapters provided in a detailed manner.

Access the NCERT Exemplar Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance

Multiple Choice Questions I

2.1. A capacitor of \(4 \, \mu\text{F}\) is connected as shown in the circuit. The internal resistance of the battery is \(0.5 \, \Omega\). The amount of charge on the capacitor plates will be: \begin{itemize} \item[(A)] \(0 \, \mu\text{C}\) \item[(B)] \(4 \, \mu\text{C}\) \item[(C)] \(16 \, \mu\text{C}\) \item[(D)] \(8 \, \mu\text{C}\) \end{itemize} \section*

{Solution} The current in the lower arm of the circuit is given by: \[ I = \frac{V}{R_{\text{total}}} = \frac{2.5 \, \text{V}}{R + 0.5 \, \Omega} \] We are given that the current \(I = 1 \, \text{A}\). Thus, \[ 1 = \frac{2.5}{R + 0.5} \] Solving for \(R\), \[ R + 0.5 = 2.5 \quad \Rightarrow \quad R = 2.0 \, \Omega \] The potential difference across the internal resistance of the battery is: \[ V_r = I \times r = 1 \, \text{A} \times 0.5 \, \Omega = 0.5 \, \text{V} \] The potential difference across the \(4 \, \mu\text{F}\) capacitor is: \[ V_C = V – V_r = 2.5 \, \text{V} – 0.5 \, \text{V} = 2 \, \text{V} \] The charge on the capacitor plates is: \[ Q = C \times V_C = 4 \, \mu\text{F} \times 2 \, \text{V} = 8 \, \mu\text{C} \] Thus, the correct option is: \begin{itemize} \item[(D)] \(8 \, \mu\text{C}\) \end{itemize}

2.2. A positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge

a) remains a constant because the electric field is uniform

b) increases because the charge moves along the electric field

c) decreases because the charge moves along the electric field

d) decreases because the charge moves opposite to the electric field

Answer:

The correct answer is c) decreases because the charge moves along the electric field

2.3. Figure shows some equipotential lines distributed in space. A charged object is moved from point \( A \) to point \( B \). \begin{itemize} \item[(A)] The work done in Fig. (ii) is least. \item[(B)] The work done in Fig. (i) is the greatest. \item[(C)] The work done is the same in Fig. (i), Fig. (ii), and Fig. (iii). \item[(D)] The work done in Fig. (iii) is greater than Fig. (ii) but equal to that in Fig. (i). \end{itemize} \section*

{Solution} The correct option is (C) The work done is the same in Fig. (i), Fig. (ii), and Fig. (iii). The work done \( W_{12} \) to move a charge \( q \) from point \( A \) to point \( B \) is given by: \[ W_{12} = q (V_2 – V_1) \] In each figure, the potential difference \( V_2 – V_1 \) between points \( A \) and \( B \) is the same, which is \( 20 \, \text{V} \). Therefore, the work done \( W \) in moving the charge from \( A \) to \( B \) will be equal in all three cases: \[ W = q \Delta V \] Thus, the work done is the same in Fig. (i), Fig. (ii), and Fig. (iii).

2.4. The electrostatic potential on the surface of a charged conducting sphere is 100V. Two statements are made in this regard:

S1: At any point inside the sphere, the electric intensity is zero

S2: At any point inside the sphere, the electrostatic potential is 100V

Which of the following is a correct statement?

a) S1 is true but S2 is false

b) Both S1 and S2 are false

c) S1 is true, S2 is also true, and S1 is the cause of S2

d) S1 is true, and S2 is also true, but the statements are independent

Answer:

The correct answer is c) S1 is true, S2 is also true, and S1 is the cause of S2

2.5. Equipotential at a great distance from a collection of charges whose total sum is not zero are approximately

a) spheres

b) planes

c) paraboloids

d) ellipsoids

Answer:

The correct answer is a) spheres

 

Multiple Choice Questions II Ncert exemplar for class 12 Physics

2.7. Consider a uniform electric field in the
direction. The potential is a constant

a) in all space

b) for any x for a given z

c) for any y for a given z

d) on the x-y plane for a given z

Answer:

The correct answer is

b) for any x for a given z

c) for any y for a given z

d) on the x-y plane for a given z

2.8. Equipotential surfaces

a) are closer in regions of large electric fields compared to regions of lower electric fields

b) will be more crowded near the sharp edges of a conductor

c) will be more crowded near regions of large charge densities

d) will always be equally spaced

Answer:

The correct answer is

a) are closer in regions of large electric fields compared to regions of lower electric fields

b) will be more crowded near the sharp edges of a conductor

c) will be more crowded near regions of large charge densities

 

2.10. In a region of constant potential

a) the electric field is uniform

b) the electric field is zero

c) there can be no charge inside the region

d) the electric field shall necessarily change if a charge is placed outside the region

Answer:

The correct answer is

b) the electric field is zero

c) there can be no charge inside the region

 

2.12. If a conductor has a potential V ≠ 0 and there are no charges anywhere else outside, then

a) there must be charges on the surface or inside itself

b) there cannot be any charge in the body of the conductor

c) there must be charges only on the surface

d) there must be charges inside the surface

Answer:

The correct answer is

a) there must be charges on the surface or inside itself

b) there cannot be any charge in the body of the conductor

 

Very Short Answers Ncert exemplar for class 12 Physics

2.15. Do free electrons travel to a region of higher potential or lower potential?

Answer:

The force on the charged particle in the electric field is F = qE

The direction of the electric field and the direction of electrostatic force experienced by the free electrons are in opposite directions

The direction of the electric field is higher than the potential, and therefore, the electrons travel from a lower potential region to a higher potential.

2.16. Can there be a potential difference between two adjacent conductors carrying the same charge?

Answer:

Yes, there can be a potential difference between two adjacent conductors carrying the same charge.

2.17. Can the potential function have a maximum or minimum in free space?

Answer:

No, the potential function cannot be maximum or minimum in free space as the absence of atmosphere around the conductor prevents the electric discharge.

2.18. A test charge \( q \) is made to move in the electric field of a point charge \( Q \) along two different closed paths (Figure). First path has sections along and perpendicular to lines of electric field. Second path is a rectangular loop of the same area as the first loop. How does the work done compare in the two cases? \section*

{Solution} The electrostatic field is conservative, which means that the work done by a conservative force in moving a charge along a closed path is zero. Here, the test charge \( q \) is moving along closed paths in the electric field created by the point charge \( Q \), and since the electric field is conservative, the work done in moving the charge along any closed path will be zero. \[ W = \oint \mathbf{E} \cdot d\mathbf{l} \] Since the electric field is conservative, the line integral of the electric field around any closed path is zero: \[ \oint \mathbf{E} \cdot d\mathbf{l} = 0 \] Thus, the work done in both the cases will be zero. \textbf{Final Answer:} As the electric field is conservative, the work done will be zero in both cases. \end{document}

Short Answers

2.19. Prove that a closed equipotential surface with no charge within itself must enclose an equipotential volume.

Answer:

In a closed equipotential surface, the potential changes from position to position.

The potential inside the surface is different from the potential gradient caused in the surface that is dV/dr

This also means that the electric field is not equal to zero, and it is given as E = -dV/dr

Therefore, it could be said that the field lines are either pointing inwards or outwards the surface.

So, it can be said that the field lines originate from the charges inside, which contradicts the original assumption. Therefore, the volume inside the surface must be equipotential.

 

2.21. Prove that if an insulated, uncharged conductor is placed near a charged conductor and no other conductors are present, the uncharged body must be intermediate in potential between that of the charged body and that of infinity.

Answer:

The electric potential decreasing along the direction of the electric field is given as E = dV/dr

The electric potential decreases when the path from the charged conductor is taken to the uncharged conductor along the direction of the electric field.

This continues when another uncharged conductor is considered to the infinity lowering the potential even further.

This shows that the uncharged body is at intermediate potential, and the charged body is at infinity potential.

 

2.23. Calculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.

Answer:

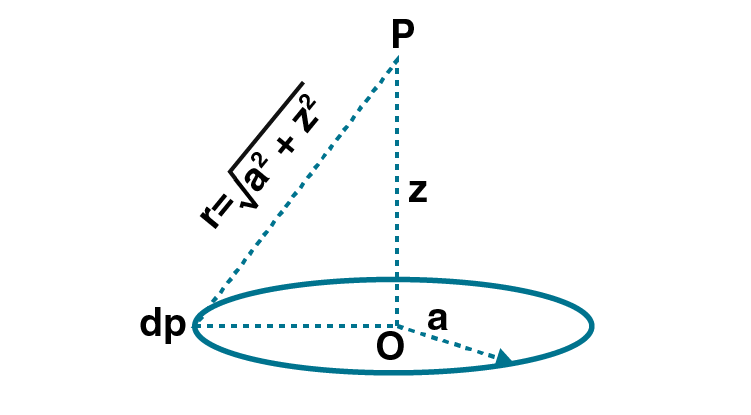
Point P is considered to be at a distance z from the centre of the ring. The charge dq is at a distance z from point P.

V is written as

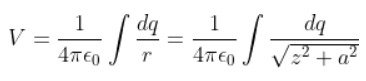
Therefore, the net potential is given as

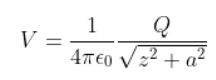
Long Answers

 

2.26. A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (U) as ε = αU where α = 2V-1. A similar capacitor with no dielectric is charged to U0 = 78 V. It is then connected to the uncharged capacitor with the dielectric. Find the final voltage on the capacitors.

Answer:

Since the capacitors are connected in parallel, the potential difference across the capacitors is the same. The final voltage is assumed to be U. C is the capacitance of the capacitor without dielectric, then the charge is given as Q1 = CU

The initial charge is given as

Q0 = CU0

The conversion of charges is

Q0 = Q1 + Q2

CU0 = CU + αCU2

αU2 + U – U0 = 0

Solving the equation, we get U = 6V

2.27. A capacitor is made of two circular plates of radius R each, separated by a distance d < < R. The capacitor is connected to a constant voltage. A thin conducting disc of radius r < < R and thickness t < < r is placed at the centre of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is m.

Answer:

When the conducting disc is placed at the centre of the bottom plate, the potential of the disc is equal to the potential of the plate. The electric field on the disc is given as

E = V/d

The charge q’ is transferred to the disc, which is given as

q’ = -ε0 V/d πr2

The force acting on the disc is

F = ε0 V2/d2 πr2

Therefore, V = square root of mdg/ π ε0r2

2.28. a) In a quark model of elementary particles, a neutron is made of one up quark and two down quarks. Assume that they have a triangle configuration with a side length of the order of 10-15 m. Calculate the electrostatic potential energy of the neutron and compare it with its mass 939 MeV.

b) Repeat the above exercise for a proton which is made of two up and one down quarks.

Answer:

There are three charges in the system. The potential energy of the system is equal to the sum of the PE of each pair.

U = 1/4 π ε0 {qdqd/r – quqd/r – quqd/r}

Substituting the values we get,

U = 5.11 10-4

2.29. Two metal spheres, one of radius R and the other of radius 2R, both have the same surface charge density σ. They are brought in contact and separated. What will be the new surface charge densities on them?

Answer:

Following are the charges on the metal sphere before contact

Q1 = σ.4πR2

Q2 = σ.4π(2R)2 = 4Q1

Q1’ and Q2’ are the charges on the metal sphere after contact

Q1’ + Q2’ = Q1 + Q2 = 5Q1

When the metal spheres are in contact, the following is the potentials acquired by them

Q1’ = Q2’/2

Solving the equations we

σ1 = 5 σ/3

σ2 = 5 σ/6

 

2.33. Two charges –q each are separated by distance 2d. A third charge +q is kept at midpoint O. Find potential energy of +q as a function of small distance x from O due to –q charges. Sketch PE versus x and convince yourself that the charge at O is in an unstable equilibrium.

Answer:

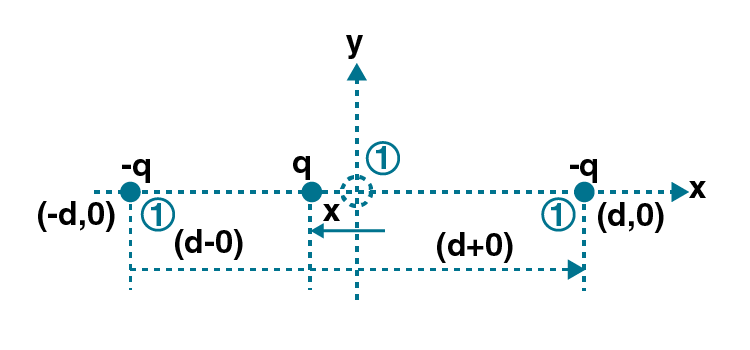
In the above figure, +q is the charge that got displaced from O towards (-d,0).

This is written as

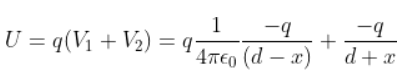
At x = 0

Differentiating the equation with respect to x, we get

When x < 0, dU/dx > 0

And when x > 0, dU/dx < 0

Using this, we can define the charge on the particle to be F = -dU/dx

F = -dU/dx = 0

When

first, d2U/dx2 = positive, equilibrium is stable

then, d2U/dx2 = negative, equilibrium is unstable

in last, d2U/dx2 = 0, equilibrium is neutral

Therefore, when x = 0, d2U/dx2 = (-2dq2/4πε0)(1/d6)(2d2) < 0

Which shows that the system is in unstable equilibrium.

NOTE: Simply helping in getting Ncert exemplar for class 12 Physics for your preparations.

NCERT Exemplar For Class 12 Science

Students must practise these additional questions for their own benefits, the ncert exemplar are curated by the best subject-matter experts to boost your knowledge on the presented topic. Students can easily access the ncert exemplar for class 12 science by visiting our website SimplyAcad and solve all the questions listed to secure maximum marks.

Here are some other NCERT exemplar for class 12 physics:

NCERT exemplar for class 12 physics Chapter 1	NCERT exemplar for class 12 physics Chapter 7
NCERT exemplar for class 12 physics Chapter 3	NCERT exemplar for class 12 physics Chapter 8
NCERT exemplar for class 12 physics Chapter 4	NCERT exemplar for class 12 physics Chapter 9
NCERT exemplar for class 12 physics Chapter 5	NCERT exemplar for class 12 physics Chapter 10
NCERT exemplar for class 12 physics Chapter 6	NCERT exemplar for class 12 physics Chapter 11