NCERT Solutions Class 11 Maths Chapter 1 Sets
NCERT Solutions for Class 11 Maths Chapter 1 – Sets
The experts at SimplyAcad have prepared the NCERT Solutions for Class 11 Maths Chapter 1 Sets. The solutions are made simple and easy to understand for students and are in accordance with CBSE guidelines.
NCERT Solutions for Class 11 Maths Chapter 1 Sets are based on the following topics:

Class 11 Maths Chapter 1- Sets Exercise 1.1
- Introduction to sets: A set is a well-defined collection of objects.
- Sets and their Representations
Class 11 Maths Chapter 1- Sets Exercise 1.2
- The Empty Set: A set which does not contain any element is called the empty set or the null set, or the void set.
- Finite and Infinite Sets: A set which is empty or consists of a definite number of elements is called finite; otherwise, the set is called infinite
- Equal Sets: Two sets, A and B, are said to be equal if they have exactly the same elements, and we write A = B. Otherwise, the sets are said to be unequal, and we write A ≠ B
Class 11 Maths Chapter 1- Sets Exercise 1.3
- Subsets: Set A is said to be a subset of a set B if every element of A is also an element of B.
- Subsets of the set of real numbers
- Intervals as subsets of R
- Power Set: The collection of all subsets of set A is called the power set of A. It is denoted by P(A).
- Universal Set: The basic set is called the “Universal Set”, which is usually denoted by U, and all its subsets by the letters A, B, C, etc
Class 11 Maths Chapter 1- Sets Exercise 1.4
- Venn Diagrams
- Operations on Sets
- Union of sets
- Intersection of sets
- Difference of sets
Class 11 Maths Chapter 1- Sets Exercise : Miscellaneous
- Sets and Their Representations
- The Empty Set, Finite and Infinite Sets, Equal Sets
- Subsets, Power Set, Universal Set
- Venn Diagrams
- Operations on Sets
- The Complement of a Set
- Practical Problems on Union and Intersection of Two Sets
The solutions to all the questions given in the textbook are provided here. The NCERT Solutions for Class 11 can help the students understand the problem-solving method thoroughly and help them to score excellent in the exam.
NCERT Solutions for Class 11 Maths Chapter 1 Sets Exercise 1.2 Solutions
1. Which of the following are examples of the null set?
(i) Set of odd natural numbers divisible by 2
(ii) Set of even prime numbers
(iii) {x: x is a natural numbers, x < 5 and x > 7}
(iv) {y: y is a point common to any two parallel lines}
Solution:
(i) Set of odd natural numbers divisible by 2 is a null set, as odd numbers are not divisible by 2.
(ii) Set of even prime numbers is not a null set, as 2 is an even prime number.
(iii) {x: x is a natural number, x < 5 and x > 7} is a null set, as a number cannot be both less than 5 and greater than 7.
(iv) {y: y is a point common to any two parallel lines} is a null set, as the parallel lines do not intersect. Therefore, they have no common point.
2. Which of the following sets are finite or infinite?
(i) The set of months of a year
(ii) {1, 2, 3 …}
(iii) {1, 2, 3 … 99, 100}
(iv) The set of positive integers greater than 100
(v) The set of prime numbers less than 99
Solution:
(i) The set of months of a year is a finite set, as it contains 12 elements.
(ii) {1, 2, 3 …} is an infinite set because it has an infinite number of natural numbers.
(iii) {1, 2, 3 …99, 100} is a finite set, as the numbers from 1 to 100 are finite.
(iv) The set of positive integers greater than 100 is an infinite set, as the positive integers, which are greater than 100, are infinite.
(v) The set of prime numbers less than 99 is a finite set, as the prime numbers which are less than 99 are finite.
3. State whether each of the following sets is finite or infinite.
(i) The set of lines which are parallel to the x-axis
(ii) The set of letters in the English alphabet
(iii) The set of numbers which are multiple of 5
(iv) The set of animals living on the earth
(v) The set of circles passing through the origin (0, 0)
Solution:
(i) The set of lines which are parallel to the x-axis is an infinite set, as the lines which are parallel to the x-axis are infinite.
(ii) The set of letters in the English alphabet is a finite set, as it contains 26 elements.
(iii) The set of numbers which are multiple of 5 is an infinite set, as the multiples of 5 are infinite.
(iv) The set of animals living on the earth is a finite set, as the number of animals living on the earth is finite.
(v) The set of circles passing through the origin (0, 0) is an infinite set, as an infinite number of circles can pass through the origin.
4. In the following, state whether A = B or not.
(i) A = {a, b, c, d}; B = {d, c, b, a}
(ii) A = {4, 8, 12, 16}; B = {8, 4, 16, 18}
(iii) A = {2, 4, 6, 8, 10}; B = {x: x is positive even integer and x ≤ 10}
(iv) A = {x: x is a multiple of 10}; B = {10, 15, 20, 25, 30 …}
Solution:
(i) A = {a, b, c, d}; B = {d, c, b, a}
The order in which the elements of a set are listed is not significant.
Therefore, A = B.
(ii) A = {4, 8, 12, 16}; B = {8, 4, 16, 18}
We know that 12 ∈ A but 12 ∉ B.
Therefore, A ≠ B
(iii) A = {2, 4, 6, 8, 10};
B = {x: x is a positive even integer and x ≤ 10} = {2, 4, 6, 8, 10}
Therefore, A = B
(iv) A = {x: x is a multiple of 10}
B = {10, 15, 20, 25, 30 …}
We know that 15 ∈ B but 15 ∉ A.
Therefore, A ≠ B
5. Are the following pair of sets equal? Give reasons.
(i) A = {2, 3}; B = {x: x is solution of x2 + 5x + 6 = 0}
(ii) A = {x: x is a letter in the word FOLLOW}; B = {y: y is a letter in the word WOLF}
Solution:
(i) A = {2, 3}; B = {x: x is solution of x2 + 5x + 6 = 0}
x2 + 5x + 6 = 0 can be written as
x(x + 3) + 2(x + 3) = 0
By further calculation,
(x + 2) (x + 3) = 0
So, we get
x = –2 or x = –3
Here,
A = {2, 3}; B = {–2, –3}
Therefore, A ≠ B
(ii) A = {x: x is a letter in the word FOLLOW} = {F, O, L, W}
B = {y: y is a letter in the word WOLF} = {W, O, L, F}
The order in which the elements of a set which are listed is not significant.
Therefore, A = B.
6. From the sets given below, select equal sets.
A = {2, 4, 8, 12}, B = {1, 2, 3, 4}, C = {4, 8, 12, 14}, D = {3, 1, 4, 2}
E = {–1, 1}, F = {0, a}, G = {1, –1}, H = {0, 1}
Solution:
A = {2, 4, 8, 12}; B = {1, 2, 3, 4}; C = {4, 8, 12, 14}
D = {3, 1, 4, 2}; E = {–1, 1}; F = {0, a}
G = {1, –1}; H = {0, 1}
We know that
8 ∈ A, 8 ∉ B, 8 ∉ D, 8 ∉ E, 8 ∉ F, 8 ∉ G, 8 ∉ H
A ≠ B, A ≠ D, A ≠ E, A ≠ F, A ≠ G, A ≠ H
It can be written as
2 ∈ A, 2 ∉ C
Therefore, A ≠ C
3 ∈ B, 3 ∉ C, 3 ∉ E, 3 ∉ F, 3 ∉ G, 3 ∉ H
B ≠ C, B ≠ E, B ≠ F, B ≠ G, B ≠ H
It can be written as
12 ∈ C, 12 ∉ D, 12 ∉ E, 12 ∉ F, 12 ∉ G, 12 ∉ H
Therefore, C ≠ D, C ≠ E, C ≠ F, C ≠ G, C ≠ H
4 ∈ D, 4 ∉ E, 4 ∉ F, 4 ∉ G, 4 ∉ H
Therefore, D ≠ E, D ≠ F, D ≠ G, D ≠ H
Here, E ≠ F, E ≠ G, E ≠ H
F ≠ G, F ≠ H, G ≠ H
The order in which the elements of a set are listed is not significant.
B = D and E = G
Therefore, among the given sets, B = D and E = G.
NCERT Solutions for Class 11 Maths Chapter 1 Sets Exercise 1.3 Solutions
1. Make correct statements by filling in the symbols ⊂ or ⊄ in the blank spaces:
(i) {2, 3, 4} … {1, 2, 3, 4, 5}
(ii) {a, b, c} … {b, c, d}
(iii) {x: x is a student of Class XI of your school} … {x: x student of your school}
(iv) {x: x is a circle in the plane} … {x: x is a circle in the same plane with radius 1 unit}
(v) {x: x is a triangle in a plane}…{x: x is a rectangle in the plane}
(vi) {x: x is an equilateral triangle in a plane}… {x: x is a triangle in the same plane}
(vii) {x: x is an even natural number} … {x: x is an integer}
Solution:
(i) {2, 3, 4} ⊂ {1, 2, 3, 4, 5}
(ii) {a, b, c} ⊄ {b, c, d}
(iii) {x: x is a student of Class XI of your school} ⊂ {x: x student of your school}
(iv) {x: x is a circle in the plane} ⊄ {x: x is a circle in the same plane with radius 1 unit}
(v) {x: x is a triangle in a plane} ⊄ {x: x is a rectangle in the plane}
(vi) {x: x is an equilateral triangle in a plane} ⊂ {x: x is a triangle in the same plane}
(vii) {x: x is an even natural number} ⊂ {x: x is an integer}
2. Examine whether the following statements are true or false:
(i) {a, b} ⊄ {b, c, a}
(ii) {a, e} ⊂ {x: x is a vowel in the English alphabet}
(iii) {1, 2, 3} ⊂ {1, 3, 5}
(iv) {a} ⊂ {a. b, c}
(v) {a} ∈ (a, b, c)
(vi) {x: x is an even natural number less than 6} ⊂ {x: x is a natural number which divides 36}
Solution:
(i) False.
Here each element of {a, b} is an element of {b, c, a}.
(ii) True.
We know that a, e are two vowels of the English alphabet.
(iii) False.
2 ∈ {1, 2, 3} where, 2∉ {1, 3, 5}
(iv) True.
Each element of {a} is also an element of {a, b, c}.
(v) False.
Elements of {a, b, c} are a, b, c. Hence, {a} ⊂ {a, b, c}
(vi) True.
{x: x is an even natural number less than 6} = {2, 4}
{x: x is a natural number which divides 36}= {1, 2, 3, 4, 6, 9, 12, 18, 36}
3. Let A = {1, 2, {3, 4}, 5}. Which of the following statements is incorrect and why?
(i) {3, 4} ⊂ A
(ii) {3, 4}}∈ A
(iii) {{3, 4}} ⊂ A
(iv) 1 ∈ A
(v) 1⊂ A
(vi) {1, 2, 5} ⊂ A
(vii) {1, 2, 5} ∈ A
(viii) {1, 2, 3} ⊂ A
(ix) Φ ∈ A
(x) Φ ⊂ A
(xi) {Φ} ⊂ A
Solution:
It is given that A = {1, 2, {3, 4}, 5}
(i) {3, 4} ⊂ A is incorrect
Here 3 ∈ {3, 4}; where, 3∉A.
(ii) {3, 4} ∈A is correct
{3, 4} is an element of A.
(iii) {{3, 4}} ⊂ A is correct
{3, 4} ∈ {{3, 4}} and {3, 4} ∈ A.
(iv) 1∈A is correct
1 is an element of A.
(v) 1⊂ A is incorrect
An element of a set can never be a subset of itself.
(vi) {1, 2, 5} ⊂ A is correct
Each element of {1, 2, 5} is also an element of A.
(vii) {1, 2, 5} ∈ A is incorrect
{1, 2, 5} is not an element of A.
(viii) {1, 2, 3} ⊂ A is incorrect
3 ∈ {1, 2, 3}; where, 3 ∉ A.
(ix) Φ ∈ A is incorrect
Φ is not an element of A.
(x) Φ ⊂ A is correct
Φ is a subset of every set.
(xi) {Φ} ⊂ A is incorrect
Φ∈ {Φ}; where, Φ ∈ A.
4. Write down all the subsets of the following sets:
(i) {a}
(ii) {a, b}
(iii) {1, 2, 3}
(iv) Φ
Solution:
(i) Subsets of {a} are
Φ and {a}.
(ii) Subsets of {a, b} are
Φ, {a}, {b}, and {a, b}.
(iii) Subsets of {1, 2, 3} are
Φ, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, and {1, 2, 3}.
(iv) Only subset of Φ is Φ.
5. How many elements has P (A), if A = Φ?
Solution:
If A is a set with m elements
n (A) = m then n [P (A)] = 2m
If A = Φ we get n (A) = 0
n [P(A)] = 20 = 1
Therefore, P (A) has one element.
6. Write the following as intervals:
(i) {x: x ∈ R, –4 < x ≤ 6}
(ii) {x: x ∈ R, –12 < x < –10}
(iii) {x: x ∈ R, 0 ≤ x < 7}
(iv) {x: x ∈ R, 3 ≤ x ≤ 4}
Solution:
(i) {x: x ∈ R, –4 < x ≤ 6} = (–4, 6]
(ii) {x: x ∈ R, –12 < x < –10} = (–12, –10)
(iii) {x: x ∈ R, 0 ≤ x < 7} = [0, 7)
(iv) {x: x ∈ R, 3 ≤ x ≤ 4} = [3, 4]
7. Write the following intervals in set-builder form:
(i) (–3, 0)
(ii) [6, 12]
(iii) (6, 12]
(iv) [–23, 5)
Solution:
(i) (–3, 0) = {x: x ∈ R, –3 < x < 0}
(ii) [6, 12] = {x: x ∈ R, 6 ≤ x ≤ 12}
(iii) (6, 12] ={x: x ∈ R, 6 < x ≤ 12}
(iv) [–23, 5) = {x: x ∈ R, –23 ≤ x < 5}
8. What universal set (s) would you propose for each of the following?
(i) The set of right triangles
(ii) The set of isosceles triangles
Solution:
(i) Among the set of right triangles, the universal set is the set of triangles or the set of polygons.
(ii) Among the set of isosceles triangles, the universal set is the set of triangles or the set of polygons or the set of two-dimensional figures.
9. Given the sets A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}, which of the following may be considered as universal set (s) for all the three sets A, B and C
(i) {0, 1, 2, 3, 4, 5, 6}
(ii) Φ
(iii) {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(iv) {1, 2, 3, 4, 5, 6, 7, 8}
Solution:
(i) We know that A ⊂ {0, 1, 2, 3, 4, 5, 6}
B ⊂ {0, 1, 2, 3, 4, 5, 6}
So C ⊄ {0, 1, 2, 3, 4, 5, 6}
Hence, the set {0, 1, 2, 3, 4, 5, 6} cannot be the universal set for the sets A, B, and C.
(ii) A ⊄ Φ, B ⊄ Φ, C ⊄ Φ
Hence, Φ cannot be the universal set for the sets A, B, and C.
(iii) A ⊂ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
B ⊂ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
C ⊂ {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Hence, the set {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} is the universal set for the sets A, B, and C.
(iv) A ⊂ {1, 2, 3, 4, 5, 6, 7, 8}
B ⊂ {1, 2, 3, 4, 5, 6, 7, 8}
So C ⊄ {1, 2, 3, 4, 5, 6, 7, 8}
Hence, the set {1, 2, 3, 4, 5, 6, 7, 8} cannot be the universal set for the sets A, B, and C
NCERT Solutions for Class 11 Maths Chapter 1 Sets Exercise 1.4 Solutions
1. Find the union of each of the following pairs of sets:
(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = {a, e, i, o, u} B = {a, b, c}
(iii) A = {x: x is a natural number and multiple of 3}
B = {x: x is a natural number less than 6}
(iv) A = {x: x is a natural number and 1 < x ≤ 6}
B = {x: x is a natural number and 6 < x < 10}
(v) A = {1, 2, 3}, B = Φ
Solution:
(i) X = {1, 3, 5} Y = {1, 2, 3}
So the union of the pairs of set can be written as
X ∪ Y= {1, 2, 3, 5}
(ii) A = {a, e, i, o, u} B = {a, b, c}
So the union of the pairs of set can be written as
A∪ B = {a, b, c, e, i, o, u}
(iii) A = {x: x is a natural number and multiple of 3} = {3, 6, 9 …}
B = {x: x is a natural number less than 6} = {1, 2, 3, 4, 5, 6}
So the union of the pairs of set can be written as
A ∪ B = {1, 2, 4, 5, 3, 6, 9, 12 …}
Hence, A ∪ B = {x: x = 1, 2, 4, 5 or a multiple of 3}
(iv) A = {x: x is a natural number and 1 < x ≤ 6} = {2, 3, 4, 5, 6}
B = {x: x is a natural number and 6 < x < 10} = {7, 8, 9}
So the union of the pairs of set can be written as
A∪ B = {2, 3, 4, 5, 6, 7, 8, 9}
Hence, A∪ B = {x: x ∈ N and 1 < x < 10}
(v) A = {1, 2, 3}, B = Φ
So the union of the pairs of set can be written as
A∪ B = {1, 2, 3}
2. Let A = {a, b}, B = {a, b, c}. Is A ⊂ B? What is A ∪ B?
Solution:
It is given that
A = {a, b} and B = {a, b, c}
Yes, A ⊂ B
So the union of the pairs of set can be written as
A∪ B = {a, b, c} = B
3. If A and B are two sets such that A ⊂ B, then what is A ∪ B?
Solution:
If A and B are two sets such that A ⊂ B, then A ∪ B = B.
4. If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10}; find
(i) A ∪ B
(ii) A ∪ C
(iii) B ∪ C
(iv) B ∪ D
(v) A ∪ B ∪ C
(vi) A ∪ B ∪ D
(vii) B ∪ C ∪ D
Solution:
It is given that
A = {1, 2, 3, 4], B = {3, 4, 5, 6}, C = {5, 6, 7, 8} and D = {7, 8, 9, 10}
(i) A ∪ B = {1, 2, 3, 4, 5, 6}
(ii) A ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
(iii) B ∪ C = {3, 4, 5, 6, 7, 8}
(iv) B ∪ D = {3, 4, 5, 6, 7, 8, 9, 10}
(v) A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
(vi) A ∪ B ∪ D = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(vii) B ∪ C ∪ D = {3, 4, 5, 6, 7, 8, 9, 10}
5. Find the intersection of each pair of sets:
(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = {a, e, i, o, u} B = {a, b, c}
(iii) A = {x: x is a natural number and multiple of 3}
B = {x: x is a natural number less than 6}
(iv) A = {x: x is a natural number and 1 < x ≤ 6}
B = {x: x is a natural number and 6 < x < 10}
(v) A = {1, 2, 3}, B = Φ
Solution:
(i) X = {1, 3, 5}, Y = {1, 2, 3}
So the intersection of the given set can be written as
X ∩ Y = {1, 3}
(ii) A = {a, e, i, o, u}, B = {a, b, c}
So the intersection of the given set can be written as
A ∩ B = {a}
(iii) A = {x: x is a natural number and multiple of 3} = (3, 6, 9 …}
B = {x: x is a natural number less than 6} = {1, 2, 3, 4, 5}
So the intersection of the given set can be written as
A ∩ B = {3}
(iv) A = {x: x is a natural number and 1 < x ≤ 6} = {2, 3, 4, 5, 6}
B = {x: x is a natural number and 6 < x < 10} = {7, 8, 9}
So the intersection of the given set can be written as
A ∩ B = Φ
(v) A = {1, 2, 3}, B = Φ
So the intersection of the given set can be written as
A ∩ B = Φ
6. If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C = {11, 13, 15} and D = {15, 17}; find
(i) A ∩ B
(ii) B ∩ C
(iii) A ∩ C ∩ D
(iv) A ∩ C
(v) B ∩ D
(vi) A ∩ (B ∪ C)
(vii) A ∩ D
(viii) A ∩ (B ∪ D)
(ix) (A ∩ B) ∩ (B ∪ C)
(x) (A ∪ D) ∩ (B ∪ C)
Solution:
(i) A ∩ B = {7, 9, 11}
(ii) B ∩ C = {11, 13}
(iii) A ∩ C ∩ D = {A ∩ C} ∩ D
= {11} ∩ {15, 17}
= Φ
(iv) A ∩ C = {11}
(v) B ∩ D = Φ
(vi) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
= {7, 9, 11} ∪ {11}
= {7, 9, 11}
(vii) A ∩ D = Φ
(viii) A ∩ (B ∪ D) = (A ∩ B) ∪ (A ∩ D)
= {7, 9, 11} ∪ Φ
= {7, 9, 11}
(ix) (A ∩ B) ∩ (B ∪ C) = {7, 9, 11} ∩ {7, 9, 11, 13, 15}
= {7, 9, 11}
(x) (A ∪ D) ∩ (B ∪ C) = {3, 5, 7, 9, 11, 15, 17) ∩ {7, 9, 11, 13, 15}
= {7, 9, 11, 15}
7. If A = {x: x is a natural number}, B ={x: x is an even natural number}
C = {x: x is an odd natural number} and D = {x: x is a prime number}, find
(i) A ∩ B
(ii) A ∩ C
(iii) A ∩ D
(iv) B ∩ C
(v) B ∩ D
(vi) C ∩ D
Solution:
It can be written as
A = {x: x is a natural number} = {1, 2, 3, 4, 5 …}
B ={x: x is an even natural number} = {2, 4, 6, 8 …}
C = {x: x is an odd natural number} = {1, 3, 5, 7, 9 …}
D = {x: x is a prime number} = {2, 3, 5, 7 …}
(i) A ∩B = {x: x is a even natural number} = B
(ii) A ∩ C = {x: x is an odd natural number} = C
(iii) A ∩ D = {x: x is a prime number} = D
(iv) B ∩ C = Φ
(v) B ∩ D = {2}
(vi) C ∩ D = {x: x is odd prime number}
8. Which of the following pairs of sets are disjoint?
(i) {1, 2, 3, 4} and {x: x is a natural number and 4 ≤ x ≤ 6}
(ii) {a, e, i, o, u}and {c, d, e, f}
(iii) {x: x is an even integer} and {x: x is an odd integer}
Solution:
(i) {1, 2, 3, 4}
{x: x is a natural number and 4 ≤ x ≤ 6} = {4, 5, 6}
So we get
{1, 2, 3, 4} ∩ {4, 5, 6} = {4}
Hence, this pair of sets is not disjoint.
(ii) {a, e, i, o, u} ∩ (c, d, e, f} = {e}
Hence, {a, e, i, o, u} and (c, d, e, f} are not disjoint.
(iii) {x: x is an even integer} ∩ {x: x is an odd integer} = Φ
Hence, this pair of sets is disjoint.
9. If A = {3, 6, 9, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20},
C = {2, 4, 6, 8, 10, 12, 14, 16}, D = {5, 10, 15, 20}; find
(i) A – B
(ii) A – C
(iii) A – D
(iv) B – A
(v) C – A
(vi) D – A
(vii) B – C
(viii) B – D
(ix) C – B
(x) D – B
(xi) C – D
(xii) D – C
Solution:
(i) A – B = {3, 6, 9, 15, 18, 21}
(ii) A – C = {3, 9, 15, 18, 21}
(iii) A – D = {3, 6, 9, 12, 18, 21}
(iv) B – A = {4, 8, 16, 20}
(v) C – A = {2, 4, 8, 10, 14, 16}
(vi) D – A = {5, 10, 20}
(vii) B – C = {20}
(viii) B – D = {4, 8, 12, 16}
(ix) C – B = {2, 6, 10, 14}
(x) D – B = {5, 10, 15}
(xi) C – D = {2, 4, 6, 8, 12, 14, 16}
(xii) D – C = {5, 15, 20}
10. If X = {a, b, c, d} and Y = {f, b, d, g}, find
(i) X – Y
(ii) Y – X
(iii) X ∩ Y
Solution:
(i) X – Y = {a, c}
(ii) Y – X = {f, g}
(iii) X ∩ Y = {b, d}
11. If R is the set of real numbers and Q is the set of rational numbers, then what is R – Q?
Solution:
We know that
R – Set of real numbers
Q – Set of rational numbers
Hence, R – Q is a set of irrational numbers.
12. State whether each of the following statement is true or false. Justify your answer.
(i) {2, 3, 4, 5} and {3, 6} are disjoint sets.
(ii) {a, e, i, o, u } and {a, b, c, d} are disjoint sets.
(iii) {2, 6, 10, 14} and {3, 7, 11, 15} are disjoint sets.
(iv) {2, 6, 10} and {3, 7, 11} are disjoint sets.
Solution:
(i) False
If 3 ∈ {2, 3, 4, 5}, 3 ∈ {3, 6}
So we get {2, 3, 4, 5} ∩ {3, 6} = {3}
(ii) False
If a ∈ {a, e, i, o, u}, a ∈ {a, b, c, d}
So we get {a, e, i, o, u} ∩ {a, b, c, d} = {a}
(iii) True
Here {2, 6, 10, 14} ∩ {3, 7, 11, 15} = Φ
(iv) True
Here {2, 6, 10} ∩ {3, 7, 11} = Φ
NCERT Solutions for Class 11 Maths Chapter 1 Sets Miscellaneous
1. Decide, among the following sets, which sets are subsets of one and another.
A= {x: x ∈ R and x satisfy x2 – 8x + 12 = 0}
B = {2, 4, 6}
C = {2, 4, 6, 8…}
D = {6}
Solution:
According to the question,
We have,
A = {x: x ∈ R and x satisfies x2 – 8x + 12 =0}
2 and 6 are the only solutions of x2 – 8x + 12 = 0
Hence, A = {2, 6}
B = {2, 4, 6}, C = {2, 4, 6, 8 …}, D = {6}
Hence, D ⊂ A ⊂ B ⊂ C
Hence, A ⊂ B, A ⊂ C, B ⊂ C, D ⊂ A, D ⊂ B, D ⊂ C
2. In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.
(i) If x ∈ A and A ∈ B, then x ∈ B
(ii) If A ⊂ B and B ∈ C, then A ∈ C
(iii) If A ⊂ B and B ⊂ C, then A ⊂ C
(iv) If A ⊄ B and B ⊄ C, then A ⊄ C
(v) If x ∈ A and A ⊄ B, then x ∈ B
(vi) If A ⊂ B and x ∉ B, then x ∉ A
Solution:
(i) False
According to the question,
A = {1, 2} and B = {1, {1, 2}, {3}}
Now, we have
2 ∈ {1, 2} and {1, 2} ∈ {1, {1, 2}, {3}}
Hence, we get
A ∈ B
We also know
{2} ∉ {1, {1, 2}, {3}}
(ii) False
According to the question,
Let us assume that
A {2}
B = {0, 2}
And, C = {1, {0, 2}, 3}
From the question,
A ⊂ B
Hence,
B ∈ C
But we know,
A ∉ C
(iii) True
According to the question,
A ⊂ B and B ⊂ C
Let us assume that
x ∈ A
Then, we have
x ∈ B
And,
x ∈ C
Therefore,
A ⊂ C
(iv) False
According to the question,
A ⊄ B
Also,
B ⊄ C
Let us assume that
A = {1, 2}
B = {0, 6, 8}
And,
C = {0, 1, 2, 6, 9}
∴ A ⊂ C
(v) False
According to the question,
x ∈ A
Also,
A ⊄ B
Let us assume that
A = {3, 5, 7}
Also,
B = {3, 4, 6}
We know that,
A ⊄ B
∴ 5 ∉ B
(vi) True
According to the question,
A ⊂ B
Also,
x ∉ B
Let us assume that
x ∈ A,
We have
x ∈ B
From the question,
We have, x ∉ B
∴ x ∉ A
3. Let A, B and C be the sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C. Show that B = C.
Solution:
According to the question,
A ∪ B = A ∪ C
And,
A ∩ B = A ∩ C
To show,
B = C
Let us assume
x ∈ B
So,
x ∈ A ∪ B
x ∈ A ∪ C
Hence,
x ∈ A or x ∈ C
When x ∈ A, then
x ∈ B
∴ x ∈ A ∩ B
As A ∩ B = A ∩ C
So, x ∈ A ∩ C
∴ x ∈ A or x ∈ C
x ∈ C
∴ B ⊂ C
Similarly, it can be shown that C ⊂ B.
Hence, B = C
4. Show that the following four conditions are equivalent.
(i) A ⊂ B (ii) A – B = Φ
(iii) A ∪ B = B (iv) A ∩ B = A
Solution:
According to the question,
To prove (i) ⬌ (ii)
Here, (i) = A ⊂ B and (ii) = A – B ≠ ϕ
Let us assume that A ⊂ B
To prove, A – B ≠ ϕ
Let A – B ≠ ϕ
Hence, there exists X ∈ A, X ≠ B, but since A⊂ B, it is not possible.
∴ A – B = ϕ
And A⊂ B ⇒ A – B ≠ ϕ
Let us assume that A – B ≠ ϕ
To prove A ⊂ B
Let X∈ A
So, X ∈ B (if X ∉ B, then A – B ≠ ϕ)
Hence, A – B = ϕ => A ⊂ B
∴ (i) ⬌ (ii)
Let us assume that A ⊂ B
To prove, A ∪ B = B
⇒ B ⊂ A ∪ B
Let us assume that x ∈ A∪ B
⇒ X ∈ A or X ∈ B
Taking Case I, X ∈ B
A ∪ B = B
Taking Case II, X ∈ A
⇒ X ∈ B (A ⊂ B)
⇒ A ∪ B ⊂ B
Let A ∪ B = B
Let us assume that X ∈ A
⇒ X ∈ A ∪ B (A ⊂ A ∪ B)
⇒ X ∈ B (A ∪ B = B)
∴ A⊂ B
Hence, (i) ⬌ (iii)
To prove (i) ⬌ (iv)
Let us assume that A ⊂ B
A ∩ B ⊂ A
Let X ∈ A
To prove, X ∈ A∩ B
Since, A ⊂ B and X ∈ B
Hence, X ∈ A ∩ B
⇒ A ⊂ A ∩ B
⇒ A = A ∩ B
Let us assume that A ∩ B = A
Let X ∈ A
⇒ X ∈ A ∩ B
⇒ X ∈ B and X ∈ A
⇒ A ⊂ B
∴ (i) ⬌ (iv)
∴ (i) ⬌ (ii) ⬌ (iii) ⬌ (iv)
Hence, proved.
5. Show that if A ⊂ B, then C – B ⊂ C – A.
Solution:
To show,
C – B ⊂ C – A
According to the question,
Let us assume that x is any element such that X ∈ C – B
∴ x ∈ C and x ∉ B
Since, A ⊂ B, we have
∴ x ∈ C and x ∉ A
So, x ∈ C – A
∴ C – B ⊂ C – A
Hence, proved.
6. Assume that P (A) = P (B). Show that A = B.
Solution:
To show,
A = B
According to the question,
P (A) = P (B)
Let x be any element of set A,
x ∈ A
Since P (A) is the power set of set A, it has all the subsets of set A.
A ∈ P (A) = P (B)
Let C be an element of set B.
For any C ∈ P (B),
We have, x ∈ C
C ⊂ B
∴ x ∈ B
∴ A ⊂ B
Similarly, we have
B ⊂ A
So, we get
If A ⊂ B and B ⊂ A
∴ A = B
7. Is it true that for any sets A and B, P (A) ∪ P (B) = P (A ∪ B)? Justify your answer.
Solution:
It is not true that for any sets A and B, P (A) ∪ P (B) = P (A ∪ B)
Justification:
Let us assume
A = {0, 1}
And, B = {1, 2}
∴ A ∪ B = {0, 1, 2}
According to the question,
We have,
P (A) = {ϕ, {0}, {1}, {0, 1}}
P (B) = {ϕ, {1}, {2}, {1, 2}}
∴ P (A ∪ B) = {ϕ, {0}, {1}, {2}, {0, 1}, {1, 2}, {0, 2}, {0, 1, 2}}
Also,
P (A) ∪ P (B) = {ϕ, {0}, {1}, {2}, {0, 1}, {1, 2}}
∴ P (A) ∪ P (B ≠ P (A ∪ B)
Hence, the given statement is false
8. Show that for any sets A and B,
A = (A ∩ B) ∪ (A – B) and A ∪ (B – A) = (A ∪ B)
Solution:
To prove,
A = (A ∩ B) ∪ (A – B)
Proof: Let x ∈ A
To show,
X ∈ (A ∩ B) ∪ (A – B)
In Case I,
X ∈ (A ∩ B)
⇒ X ∈ (A ∩ B) ⊂ (A ∪ B) ∪ (A – B)
In Case II,
X ∉A ∩ B
⇒ X ∉ B or X ∉ A
⇒ X ∉ B (X ∉ A)
⇒ X ∉ A – B ⊂ (A ∪ B) ∪ (A – B)
∴A ⊂ (A ∩ B) ∪ (A – B) (i)
It can be concluded that A ∩ B ⊂ A and (A – B) ⊂ A
Thus, (A ∩ B) ∪ (A – B) ⊂ A (ii)
Equating (i) and (ii),
A = (A ∩ B) ∪ (A – B)
We also have to show
A ∪ (B – A) ⊂ A ∪ B
Let us assume
X ∈ A ∪ (B – A)
X ∈ A or X ∈ (B – A)
⇒ X ∈ A or (X ∈ B and X ∉A)
⇒ (X ∈ A or X ∈ B) and (X ∈ A and X ∉A)
⇒ X ∈ (B ∪A)
∴ A ∪ (B – A) ⊂ (A ∪ B) (iii)
According to the question,
To prove:
(A ∪ B) ⊂ A ∪ (B – A)
Let y ∈ A∪B
Y ∈ A or y ∈ B
(y ∈ A or y ∈ B) and (X ∈ A and X ∉A)
⇒ y ∈ A or (y ∈ B and y ∉A)
⇒ y ∈ A ∪ (B – A)
Thus, A ∪ B ⊂ A ∪ (B – A) (iv)
∴ From equations (iii) and (iv), we get
A ∪ (B – A) = A ∪ B
9. Using properties of sets, show that
(i) A ∪ (A ∩ B) = A
(ii) A ∩ (A ∪ B) = A
Solution:
(i) To show: A ∪ (A ∩ B) = A
We know that,
A ⊂ A
A ∩ B ⊂ A
∴ A ∪ (A ∩ B) ⊂ A (i)
Also, according to the question,
We have
A⊂ A ∪ (A ∩ B) (ii)
Hence, from equations (i) and (ii),
We have
A ∪ (A ∩ B) = A
(ii) To show,
A ∩ (A ∪ B) = A
A ∩ (A ∪ B) = (A ∩ A) ∪ (A ∩ B)
= A ∪ (A ∩ B)
= A
10. Show that A ∩ B = A ∩ C need not imply B = C.
Solution:
Let us assume,
A = {0, 1}
B = {0, 2, 3}
And, C = {0, 4, 5}
According to the question,
A ∩ B = {0}
And,
A ∩ C = {0}
∴ A ∩ B = A ∩ C = {0}
But,
2 ∈ B and 2 ∉ C
Therefore, B ≠ C
11. Let A and B be sets. If A ∩ X = B ∩ X = ϕ and A ∪ X = B ∪ X for some set X, show that A = B.
(Hints: A = A ∩ (A ∪ X) , B = B ∩ (B ∪ X), and use Distributive law.)
Solution:
According to the question,
Let A and B be two sets such that A ∩ X = B ∩ X = ϕ and A ∪ X = B ∪ X for some set X.
To show, A = B
Proof:
A = A ∩ (A ∪ X) = A ∩ (B ∪ X) [A ∪ X = B ∪ X]
= (A ∩ B) ∪ (A ∩ X) [Distributive law]
= (A ∩ B) ∪ Φ [A ∩ X = Φ]
= A ∩ B (i)
Now, B = B ∩ (B ∪ X)
= B ∩ (A ∪ X) [A ∪ X = B ∪ X]
= (B ∩ A) ∪ (B ∩ X) … [Distributive law]
= (B ∩ A) ∪ Φ [B ∩ X = Φ]
= A ∩ B (i)
Hence, from equations (i) and (ii), we obtain A = B
12. Find sets A, B and C such that A ∩ B, B ∩ C and A ∩ C are non-empty sets and A ∩ B ∩ C = Φ.
Solution:
Let us assume, A {0, 1}
B = {1, 2}
And, C = {2, 0}
According to the question,
A ∩ B = {1}
B ∩ C = {2}
And,
A ∩ C = {0}
∴ A ∩ B, B ∩ C and A ∩ C are not empty sets.
Hence, we get
A ∩ B ∩ C = Φ
13. In a survey of 600 students in a school, 150 students were found to be taking tea, and 225 were taking coffee, 100 were taking both tea and coffee. Find how many students were taking neither tea nor coffee.
Solution:
Let us assume that,
U = The set of all students who took part in the survey
T = The set of students taking tea
C = The set of students taking coffee
Total number of students in a school, n (U) = 600
Number of students taking tea, n (T) = 150
Number of students taking coffee, n (C) = 225
Also, n (T ∩ C) = 100
Now, we have to find the number of students taking neither coffee nor tea, i.e., n (T ∩ C’)
∴ According to the question,
n ( T ∩ C’ )= n( T ∩ C )’
= n (U) – n (T ∩ C)
= n (U) – [n (T) + n(C) – n (T ∩ C)]
= 600 – [150 + 225 – 100]
= 600 – 275
= 325
∴ Number of students taking neither coffee nor tea = 325 students
14. In a group of students, 100 students know Hindi, 50 know English and 25 know both. Each of the students knows either Hindi or English. How many students are there in the group?
Solution:
Let us assume that,
U = The set of all students in the group
E = The set of students who know English
H = The set of students who know Hindi
∴ H ∪ E = U
Given that,
Number of students who know Hindi n (H) = 100
Number of students who know English, n (E) = 50
Number of students who know both, n (H ∩ E) = 25
We have to find the total number of students in the group, i.e., n (U)
∴ According to the question,
n (U) = n(H) + n(E) – n(H ∩ E)
= 100 + 50 – 25
= 125
∴ Total number of students in the group = 125 students
15. In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read newspaper I, 9 read both H and I, 11 read both H and T, 8 read both T and I, 3 read all three newspapers. Find:
(i) The number of people who read at least one of the newspapers.
(ii) The number of people who read exactly one newspaper.
Solution:
(i) Let us assume that,
A = The set of people who read newspaper H
B = The set of people who read newspaper T
C = The set of people who read newspaper I
According to the question,
Number of people who read newspaper H, n (A) = 25
Number of people who read newspaper T, n (B) = 26
Number of people who read the newspaper I, n (C) = 26
Number of people who read both newspaper H and I, n (A ∩ C) = 9
Number of people who read both newspaper H and T, n (A ∩ B) = 11
Number of people who read both newspaper T and I, n (B ∩ C) = 8
And, the number of people who read all three newspapers H, T and I, n (A ∩ B ∩ C) = 3
Now, we have to find the number of people who read at least one of the newspapers
∴, we get
![]()
= 25 + 26 + 26 – 11 – 8 – 9 + 3
= 80 – 28
= 52
∴ There are a total of 52 students who read at least one newspaper.
(ii) Let us assume that,
a = The number of people who read newspapers H and T only
b = The number of people who read newspapers I and H only
c = The number of people who read newspapers T and I only
d = The number of people who read all three newspapers
According to the question,
D = n(A ∩ B ∩ C) = 3
Now, we have
n(A ∩ B) = a + d
n(B ∩ C) = c + d
And,
n(C ∩ A) = b + d
∴ a + d + c +d + b + d = 11 + 8 + 9
a + b + c + d = 28 – 2d
= 28 – 6
= 22
∴ The number of people who read exactly one newspaper = 52 – 22
= 30 people
16. In a survey, it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C, and 8 liked all three products. Find how many liked product C only.
Solution:
Let A, B and C = the set of people who like product A, product B and product C, respectively.
Now, according to the question,
Number of students who like product A, n (A) = 21
Number of students who like product B, n (B) = 26
Number of students who like product C, n (C) = 29
Number of students who like both products A and B, n (A ∩ B) = 14
Number of students who like both products A and C, n (C ∩ A) = 12
Number of students who like both products C and B, n (B ∩ C) = 14
Number of students who like all three products, n (A ∩ B ∩ C) = 8
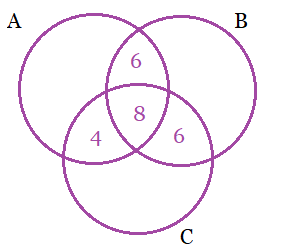
From the Venn diagram, we get
Number of students who only like product C = {29 – (4 + 8 + 6)}
= {29 – 18}
= 11 students
latest video
news via inbox
Nulla turp dis cursus. Integer liberos euismod pretium faucibua




