Octants	I	II	III	IV	V	VI	VII	VIII
x	+	–	–	+	+	–	–	+
y	+	+	–	–	+	+	–	–
z	+	+	+	+	–	–	–	–

(i) (1, 2, 3)

Here, x is positive, y is positive, and z is positive.

So, it lies in the I octant.

(ii) (4, -2, 3)

Here, x is positive, y is negative, and z is positive.

So, it lies in the IV octant.

(iii) (4, -2, -5)

Here, x is positive, y is negative, and z is negative.

So, it lies in the VIII octant.

(iv) (4, 2, -5)

Here, x is positive, y is positive, and z is negative.

So, it lies in the V octant.

(v) (-4, 2, -5)

Here, x is negative, y is positive, and z is negative.

So, it lies in VI octant.

(vi) (-4, 2, 5)

Here, x is negative, y is positive, and z is positive.

So, it lies in the II octant.

(vii) (-3, -1, 6)

Here, x is negative, y is negative, and z is positive.

So, it lies in the III octant.

(viii) (2, -4, -7)

Here, x is positive, y is negative, and z is negative.

So, it lies in the VIII octant.

4. Fill in the blanks:
(i) The x-axis and y-axis, taken together, determine a plane known as _______.
(ii) The coordinates of points in the XY-plane are of the form _______.
(iii) Coordinate planes divide the space into ______ octants.

Solution:

(i) The x-axis and y-axis, taken together, determine a plane known as XY Plane.

(ii) The coordinates of points in the XY-plane are of the form (x, y, 0).

(iii) Coordinate planes divide the space into eight octants.

NCERT Solutions for Class 11 Maths Chapter 11 Introduction to Three Dimensional Geometry Exercise 11.2

1. Find the distance between the following pairs of points:

(i) (2, 3, 5) and (4, 3, 1)

(ii) (–3, 7, 2) and (2, 4, –1)

(iii) (–1, 3, –4) and (1, –3, 4)

(iv) (2, –1, 3) and (–2, 1, 3)

Solution:

(i) (2, 3, 5) and (4, 3, 1)

Let P be (2, 3, 5) and Q be (4, 3, 1)

By using the formula,

Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = 2, y1 = 3, z1 = 5

x2 = 4, y2 = 3, z2 = 1

Distance PQ = √[(4 – 2)2 + (3 – 3)2 + (1 – 5)2]

= √[(2)2 + 02 + (-4)2]

= √[4 + 0 + 16]

= √20

= 2√5

∴ The required distance is 2√5 units.

(ii) (–3, 7, 2) and (2, 4, –1)

Let P be (– 3, 7, 2) and Q be (2, 4, –1)

By using the formula,

Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = – 3, y1 = 7, z1 = 2

x2 = 2, y2 = 4, z2 = – 1

Distance PQ = √[(2 – (-3))2 + (4 – 7)2 + (-1 – 2)2]

= √[(5)2 + (-3)2 + (-3)2]

= √[25 + 9 + 9]

= √43

∴ The required distance is √43 units.

(iii) (–1, 3, –4) and (1, –3, 4)

Let P be (– 1, 3, – 4) and Q be (1, – 3, 4)

By using the formula,

Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So here,

x1 = – 1, y1 = 3, z1 = – 4

x2 = 1, y2 = – 3, z2 = 4

Distance PQ = √[(1 – (-1))2 + (-3 – 3)2 + (4 – (-4))2]

= √[(2)2 + (-6)2 + (8)2]

= √[4 + 36 + 64]

= √104

= 2√26

∴ The required distance is 2√26 units.

(iv) (2, –1, 3) and (–2, 1, 3)

Let P be (2, – 1, 3) and Q be (– 2, 1, 3)

By using the formula,

Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So here,

x1 = 2, y1 = – 1, z1 = 3

x2 = – 2, y2 = 1, z2 = 3

Distance PQ = √[(-2 – 2)2 + (1 – (-1))2 + (3 – 3)2]

= √[(-4)2 + (2)2 + (0)2]

= √[16 + 4 + 0]

= √20

= 2√5

∴ The required distance is 2√5 units.

2. Show that the points (–2, 3, 5), (1, 2, 3) and (7, 0, –1) are collinear.

Solution:

If three points are collinear, then they lie on the same line.

First, let us calculate the distance between the 3 points

i.e., PQ, QR and PR

Calculating PQ

P ≡ (–2, 3, 5) and Q ≡ (1, 2, 3)

By using the formula,

Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = – 2, y1 = 3, z1 = 5

x2 = 1, y2 = 2, z2 = 3

Distance PQ = √[(1 – (-2))2 + (2 – 3)2 + (3 – 5)2]

= √[(3)2 + (-1)2 + (-2)2]

= √[9 + 1 + 4]

= √14

Calculating QR

Q ≡ (1, 2, 3) and R ≡ (7, 0, – 1)

By using the formula,

Distance QR = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = 1, y1 = 2, z1 = 3

x2 = 7, y2 = 0, z2 = – 1

Distance QR = √[(7 – 1)2 + (0 – 2)2 + (-1 – 3)2]

= √[(6)2 + (-2)2 + (-4)2]

= √[36 + 4 + 16]

= √56

= 2√14

Calculating PR

P ≡ (–2, 3, 5) and R ≡ (7, 0, – 1)

By using the formula,

Distance PR = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So here,

x1 = –2, y1 = 3, z1 = 5

x2 = 7, y2 = 0, z2 = –1

Distance PR = √[(7 – (-2))2 + (0 – 3)2 + (-1 – 5)2]

= √[(9)2 + (-3)2 + (-6)2]

= √[81 + 9 + 36]

= √126

= 3√14

Thus, PQ = √14, QR = 2√14 and PR = 3√14

So, PQ + QR = √14 + 2√14

= 3√14

= PR

∴ The points P, Q and R are collinear.

3. Verify the following:
(i) (0, 7, –10), (1, 6, –6), and (4, 9, –6) are the vertices of an isosceles triangle.

(ii) (0, 7, 10), (–1, 6, 6), and (–4, 9, 6) are the vertices of a right-angled triangle.

(iii) (–1, 2, 1), (1, –2, 5), (4, –7, 8), and (2, –3, 4) are the vertices of a parallelogram.

Solution:

(i) (0, 7, –10), (1, 6, –6), and (4, 9, – 6) are the vertices of an isosceles triangle.

Let us consider the points,

P(0, 7, –10), Q(1, 6, –6) and R(4, 9, –6)

If any 2 sides are equal, it will be an isosceles triangle

So, first, let us calculate the distance of PQ, QR

Calculating PQ

P ≡ (0, 7, – 10) and Q ≡ (1, 6, – 6)

By using the formula,

Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here,

x1 = 0, y1 = 7, z1 = – 10

x2 = 1, y2 = 6, z2 = – 6

Distance PQ = √[(1 – 0)2 + (6 – 7)2 + (-6 – (-10))2]

= √[(1)2 + (-1)2 + (4)2]

= √[1 + 1 + 16]

= √18

Calculating QR

Q ≡ (1, 6, – 6) and R ≡ (4, 9, – 6)

By using the formula,

Distance QR = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = 1, y1 = 6, z1 = – 6

x2 = 4, y2 = 9, z2 = – 6

Distance QR = √[(4 – 1)2 + (9 – 6)2 + (-6 – (-6))2]

= √[(3)2 + (3)2 + (-6+6)2]

= √[9 + 9 + 0]

= √18

Hence, PQ = QR

18 = 18

2 sides are equal

∴ PQR is an isosceles triangle.

(ii) (0, 7, 10), (–1, 6, 6), and (–4, 9, 6) are the vertices of a right-angled triangle.

Let the points be

P(0, 7, 10), Q(– 1, 6, 6) & R(– 4, 9, 6)

First, let us calculate the distance of PQ, OR and PR

Calculating PQ

P ≡ (0, 7, 10) and Q ≡ (– 1, 6, 6)

By using the formula,

Distance PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So here,

x1 = 0, y1 = 7, z1 = 10

x2 = –1, y2 = 6, z2 = 6

Distance PQ = √[(-1 – 0)2 + (6 – 7)2 + (6 – 10)2]

= √[(-1)2 + (-1)2 + (-4)2]

= √[1 + 1 + 16]

= √18

Calculating QR

Q ≡ (1, 6, –6) and R ≡ (4, 9, –6)

By using the formula,

Distance QR = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = 1, y1 = 6, z1 = –6

x2 = 4, y2 = 9, z2 = –6

Distance QR = √[(4 – 1)2 + (9 – 6)2 + (-6 – (-6))2]

= √[(3)2 + (3)2 + (-6+6)2]

= √[9 + 9 + 0]

= √18

Calculating PR

P ≡ (0, 7, 10) and R ≡ (– 4, 9, 6)

By using the formula,

Distance PR = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = 0, y1 = 7, z1 = 10

x2 = – 4, y2 = 9, z2 = 6

Distance PR = √[(-4 – 0)2 + (9 – 7)2 + (6 – 10)2]

= √[(-4)2 + (2)2 + (-4)2]

= √[16 + 4 + 16]

= √36

Now,

PQ2 + QR2 = 18 + 18

= 36

= PR2

By using the converse of Pythagoras theorem,

∴ The given vertices P, Q & R are the vertices of a right–angled triangle at Q.

(iii) (–1, 2, 1), (1, –2, 5), (4, –7, 8), and (2, –3, 4) are the vertices of a parallelogram.

Let the points: A(–1, 2, 1), B(1, –2, 5), C(4, –7, 8) & D(2, –3, 4)

ABCD can be vertices of parallelogram only if opposite sides are equal.

i.e., AB = CD and BC = AD

First, let us calculate the distance

Calculating AB

A ≡ (–1, 2, 1) and B ≡ (1, –2, 5)

By using the formula,

Distance AB = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = – 1, y1 = 2, z1 = 1

x2 = 1, y2 = – 2, z2 = 5

Distance AB = √[(1 – (-1))2 + (-2 – 2)2 + (5 – 1)2]

= √[(2)2 + (-4)2 + (4)2]

= √[4 + 16 + 16]

= √36

= 6

Calculating BC

B ≡ (1, –2, 5) and C ≡ (4, –7, 8)

By using the formula,

Distance BC = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = 1, y1 = – 2, z1 = 5

x2 = 4, y2 = – 7, z2 = 8

Distance BC = √[(4 – 1)2 + (-7 – (-2))2 + (8 – 5)2]

= √[(3)2 + (-5)2 + (3)2]

= √[9 + 25 + 9]

= √43

Calculating CD

C ≡ (4, –7, 8) and D ≡ (2, –3, 4)

By using the formula,

Distance CD = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So here,

x1 = 4, y1 = –7, z1 = 8

x2 = 2, y2 = –3, z2 = 4

Distance CD = √[(2 – 4)2 + (-3 – (-7))2 + (4 – 8)2]

= √[(-2)2 + (4)2 + (-4)2]

= √[4 + 16 + 16]

= √36

= 6

Calculating DA

D ≡ (2, –3, 4) and A ≡ (–1, 2, 1)

By using the formula,

Distance DA = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = 2, y1 = – 3, z1 = 4

x2 = –1, y2 = 2, z2 = 1

Distance DA = √[(-1 – 2)2 + (2 – (-3))2 + (1 – 4)2]

= √[(-3)2 + (5)2 + (-3)2]

= √[9 + 25 + 9]

= √43

Since AB = CD and BC = DA (given),

In ABCD, both pairs of opposite sides are equal.

∴ ABCD is a parallelogram.

4. Find the equation of the set of points which are equidistant from the points (1, 2, 3) and (3, 2, –1).

Solution:

Let A (1, 2, 3) & B (3, 2, –1)

Let point P be (x, y, z)

Since it is given that point P(x, y, z) is equal distance from point A(1, 2, 3) & B(3, 2, –1)

i.e. PA = PB

First, let us calculate

Calculating PA

P ≡ (x, y, z) and A ≡ (1, 2, 3)

By using the formula,

Distance PA = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = x, y1 = y, z1 = z

x2 = 1, y2 = 2, z2 = 3

Distance PA = √[(1 – x)2 + (2 – y)2 + (3 – z)2]

Calculating PB

P ≡ (x, y, z) and B ≡ (3, 2, –1)

By using the formula,

Distance PB = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = x, y1 = y, z1 = z

x2 = 3, y2 = 2, z2 = –1

Distance PB = √[(3 – x)2 + (2 – y)2 + (-1 – z)2]

Since PA = PB

Square on both sides, we get

PA2 = PB2

(1 – x)2 + (2 – y)2 + (3 – z)2 = (3 – x)2 + (2 – y)2 + (– 1 – z)2

(1 + x2 – 2x) + (4 + y2 – 4y) + (9 + z2 – 6z)

(9 + x2 – 6x) + (4 + y2 – 4y) + (1 + z2 + 2z)

– 2x – 4y – 6z + 14 = – 6x – 4y + 2z + 14

4x – 8z = 0

x – 2z = 0

∴ The required equation is x – 2z = 0.

5. Find the equation of the set of points P, the sum of whose distances from A(4, 0, 0) and B(–4, 0, 0) is equal to 10.

Solution:

Let A(4, 0, 0) & B(– 4, 0, 0)

Let the coordinates of point P be (x, y, z)

Calculating PA

P ≡ (x, y, z) and A ≡ (4, 0, 0)

By using the formula,

Distance PA = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, here

x1 = x, y1 = y, z1 = z

x2 = 4, y2 = 0, z2 = 0

Distance PA = √[(4– x)2 + (0 – y)2 + (0 – z)2]

Calculating PB,

P ≡ (x, y, z) and B ≡ (– 4, 0, 0)

By using the formula,

Distance PB = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So here,

x1 = x, y1 = y, z1 = z

x2 = – 4, y2 = 0, z2 = 0

Distance PB = √[(-4– x)2 + (0 – y)2 + (0 – z)2]

It is given that,

PA + PB = 10

PA = 10 – PB

Square on both sides, we get

PA2 = (10 – PB)2

PA2 = 100 + PB2 – 20 PB

(4 – x)2 + (0 – y)2 + (0 – z)2

100 + (– 4 – x)2 + (0 – y)2 + (0 – z)2 – 20 PB

(16 + x2 – 8x) + (y2) + (z2)

100 + (16 + x2 + 8x) + (y2) + (z2) – 20 PB

20 PB = 16x + 100

5 PB = (4x + 25)

Square on both sides again, we get

25 PB2 = 16×2 + 200x + 625

25 [(– 4 – x)2 + (0 – y)2 + (0 – z)2] = 16×2 + 200x + 625

25 [x2 + y2 + z2 + 8x + 16] = 16×2 + 200x + 625

25×2 + 25y2 + 25z2 + 200x + 400 = 16×2 + 200x + 625

9×2 + 25y2 + 25z2 – 225 = 0

∴ The required equation is 9×2 + 25y2 + 25z2 – 225 = 0.

NCERT Solutions for Class 11 Maths Chapter 11 Introduction to Three Dimensional Geometry Exercise 11.3

1. Find the coordinates of the point which divides the line segment joining the points (–2, 3, 5) and (1, –4, 6) in the ratio (i) 2:3 internally, (ii) 2:3 externally.

Solution:

Let the line segment joining the points P (-2, 3, 5) and Q (1, -4, 6) be PQ.

(i) 2:3 internally

By using the section formula,

We know that the coordinates of the point R, which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) internally in the ratio m:n, is given by:

Upon comparing, we have

x1 = -2, y1 = 3, z1 = 5;

x2 = 1, y2 = -4, z2 = 6 and

m = 2, n = 3

So, the coordinates of the point which divide the line segment joining the points P (– 2, 3, 5) and Q (1, – 4, 6) in the ratio 2:3 internally is given by:

Hence, the coordinates of the point which divides the line segment joining the points (-2, 3, 5) and (1, -4, 6) is (-4/5, 1/5, 27/5).

(ii) 2:3 externally

By using the section formula,

We know that the coordinates of the point R, which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) externally in the ratio m:n, is given by:

Upon comparing, we have

x1 = -2, y1 = 3, z1 = 5;

x2 = 1, y2 = -4, z2 = 6 and

m = 2, n = 3

So, the coordinates of the point which divide the line segment joining the points P (–2, 3, 5) and Q (1, –4, 6) in the ratio 2:3 externally is given by:

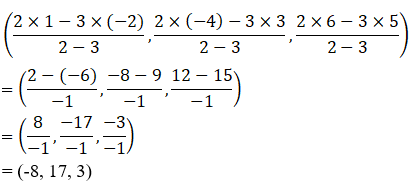
∴ The coordinates of the point which divides the line segment joining the points (-2, 3, 5) and (1, -4, 6) is (-8, 17, 3).

2. Given that P (3, 2, –4), Q (5, 4, –6) and R (9, 8, –10) are collinear. Find the ratio in which Q divides PR.

Solution:

Let us consider Q divides PR in the ratio k:1.

By using the section formula,

We know that the coordinates of the point R, which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) internally in the ratio m:n, is given by:

Upon comparing, we have,

x1 = 3, y1 = 2, z1 = -4;

x2 = 9, y2 = 8, z2 = -10 and

m = k, n = 1

So, we have

9k + 3 = 5 (k+1)

9k + 3 = 5k + 5

9k – 5k = 5 – 3

4k = 2

k = 2/4

= ½

Hence, the ratio in which Q divides PR is 1:2.

3. Find the ratio in which the YZ-plane divides the line segment formed by joining the points (–2, 4, 7) and (3, –5, 8).

Solution:

Let the line segment formed by joining the points P (-2, 4, 7) and Q (3, -5, 8) be PQ.

We know that any point on the YZ-plane is of the form (0, y, z).

So, let R (0, y, z) divides the line segment PQ in the ratio k:1.

Then,

Upon comparing, we have,

x1 = -2, y1 = 4, z1 = 7;

x2 = 3, y2 = -5, z2 = 8 and

m = k, n = 1

By using the section formula,

We know that the coordinates of the point R, which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) internally in the ratio m:n, is given by:

So we have,

3k – 2 = 0

3k = 2

k = 2/3

Hence, the ratio in which the YZ-plane divides the line segment formed by joining the points (–2, 4, 7) and (3, –5, 8) is 2:3.

4. Using the section formula, show that the points A (2, –3, 4), B (–1, 2, 1) and C (0, 1/3, 2) are collinear.

Solution:

Let point P divides AB in the ratio k:1.

Upon comparing, we have,

x1 = 2, y1 = -3, z1 = 4;

x2 = -1, y2 = 2, z2 = 1 and

m = k, n = 1

By using the section formula,

We know that the coordinates of the point R, which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) internally in the ratio m:n, is given by:

So we have,

Now, we check if, for some value of k, the point coincides with point C.

Put (-k+2)/(k+1) = 0

-k + 2 = 0

k = 2

When k = 2, then (2k-3)/(k+1) = (2(2)-3)/(2+1)

= (4-3)/3

= 1/3

And, (k+4)/(k+1) = (2+4)/(2+1)

= 6/3

= 2

∴ C (0, 1/3, 2) is a point which divides AB in the ratio 2:1 and is the same as P.

Hence, A, B, and C are collinear.

5. Find the coordinates of the points which trisect the line segment joining the points P (4, 2, –6) and Q (10, –16, 6).

Solution:

Let A (x1, y1, z1) and B (x2, y2, z2) trisect the line segment joining the points P (4, 2, -6) and Q (10, -16, 6).

A divides the line segment PQ in the ratio 1:2.

Upon comparing, we have,

x1 = 4, y1 = 2, z1 = -6;

x2 = 10, y2 = -16, z2 = 6 and

m = 1, n = 2

By using the section formula,

We know that the coordinates of the point R, which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) internally in the ratio m:n, is given by:

So, we have

Similarly, we know that B divides the line segment PQ in the ratio 2:1.

Upon comparing, we have,

x1 = 4, y1 = 2, z1 = -6;

x2 = 10, y2 = -16, z2 = 6 and

m = 2, n = 1

By using the section formula,

We know that the coordinates of the point R, which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) internally in the ratio m:n, is given by:

So, we have

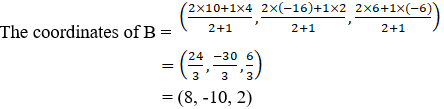
∴ The coordinates of the points which trisect the line segment joining the points P (4, 2, – 6) and Q (10, –16, 6) are (6, -4, -2) and (8, -10, 2).

NCERT Solutions for Class 11 Maths Chapter 11 Introduction to Three Dimensional Geometry Miscellaneous Exercise

1. Three vertices of a parallelogram ABCD are A(3, – 1, 2), B(1, 2, – 4) and C(– 1, 1, 2). Find the coordinates of the fourth vertex.

Solution:

Given:

ABCD is a parallelogram with vertices A (3, -1, 2), B (1, 2, -4), and C (-1, 1, 2).

Where, x1 = 3, y1 = -1, z1 = 2;

x2 = 1, y2 = 2, z2 = -4;

x3 = -1, y3 = 1, z3 = 2

Let the coordinates of the fourth vertex be D (x, y, z).

We know that the diagonals of a parallelogram bisect each other, so the midpoints of AC and BD are equal, i.e., Midpoint of AC = Midpoint of BD ……….(1)

Now, by the midpoint formula, we know that the coordinates of the mid-point of the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) are [(x1+x2)/2, (y1+y2)/2, (z1+z2)/2]

So we have,

= (2/2, 0/2, 4/2)

= (1, 0, 2)

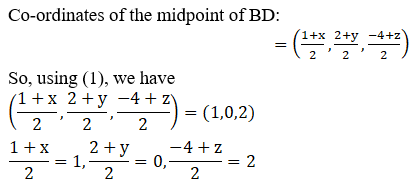
1 + x = 2, 2 + y = 0, -4 + z = 4

x = 1, y = -2, z = 8

Hence, the coordinates of the fourth vertex are D (1, -2, 8).

2. Find the lengths of the medians of the triangle with vertices A (0, 0, 6), B (0, 4, 0) and C (6, 0, 0).

Solution:

Given:

The vertices of the triangle are A (0, 0, 6), B (0, 4, 0) and C (6, 0, 0).

x1 = 0, y1 = 0, z1 = 6;

x2 = 0, y2 = 4, z2 = 0;

x3 = 6, y3 = 0, z3 = 0

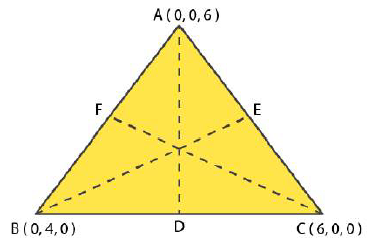
So, let the medians of this triangle be AD, BE and CF, corresponding to the vertices A, B and C, respectively.

D, E and F are the midpoints of the sides BC, AC and AB, respectively.

By the midpoint formula, the coordinates of the midpoint of the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) are [(x1+x2)/2, (y1+y2)/2, (z1+z2)/2]

So, we have

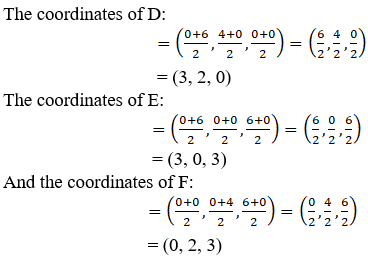
By the distance formula, the distance between two points P (x1, y1, z1) and Q (x2, y2, z2) is given by

∴ The lengths of the medians of the given triangle are 7, √34 and 7.

3. If the origin is the centroid of the triangle PQR with vertices P (2a, 2, 6), Q (–4, 3b, –10) and R (8, 14, 2c), then find the values of a, b and c.

Solution:

Given:

The vertices of the triangle are P (2a, 2, 6), Q (-4, 3b, -10) and R (8, 14, 2c).

Where,

x1 = 2a, y1 = 2, z1 = 6;

x2 = -4, y2 = 3b, z2 = -10;

x3 = 8, y3 = 14, z3 = 2c

We know that the coordinates of the centroid of the triangle, whose vertices are (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3), are [(x1+x2+x3)/3, (y1+y2+y3)/3, (z1+z2+z3)/3]

So, the coordinates of the centroid of the triangle PQR are

2a + 4 = 0, 3b + 16 = 0, 2c – 4 = 0

a = -2, b = -16/3, c = 2

∴ The values of a, b and c are a = -2, b = -16/3, and c = 2.

4. Find the coordinates of a point on the y-axis, which are at a distance of 5√2 from the point P (3, –2, 5).

Solution:

Let the point on the y-axis be A (0, y, 0).

Then, it is given that the distance between the points A (0, y, 0) and P (3, -2, 5) is 5√2.

Now, by using the distance formula,

We know that the distance between two points P (x1, y1, z1) and Q (x2, y2, z2) is given by

Distance of PQ = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

So, the distance between the points A (0, y, 0) and P (3, -2, 5) is given by

Distance of AP = √[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

= √[(3-0)2 + (-2-y)2 + (5-0)2]

= √[32 + (-2-y)2 + 52]

= √[(-2-y)2 + 9 + 25]

5√2 = √[(-2-y)2 + 34]

Squaring on both sides, we get

(-2 -y)2 + 34 = 25 × 2

(-2 -y)2 = 50 – 34

4 + y2 + (2 × -2 × -y) = 16

y2 + 4y + 4 -16 = 0

y2 + 4y – 12 = 0

y2 + 6y – 2y – 12 = 0

y (y + 6) – 2 (y + 6) = 0

(y + 6) (y – 2) = 0

y = -6, y = 2

∴ The points (0, 2, 0) and (0, -6, 0) are the required points on the y-axis.

5. A point R with x-coordinate 4 lies on the line segment joining the points P (2, –3, 4) and Q (8, 0, 10). Find the coordinates of the point R.[Hint: Suppose R divides PQ in the ratio k:1. The coordinates of the point R are given by

Solution:

Given:

The coordinates of the points are P (2, -3, 4) and Q (8, 0, 10).

x1 = 2, y1 = -3, z1 = 4;

x2 = 8, y2 = 0, z2 = 10

Let the coordinates of the required point be (4, y, z).

So, let the point R (4, y, z) divides the line segment joining the points P (2, -3, 4) and Q (8, 0, 10) in the ratio k:1.

By using the section formula,

We know that the coordinates of the point R, which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) internally in the ratio m:n, is given by:

So, the coordinates of the point R are given by

So, we have

8k + 2 = 4 (k + 1)

8k + 2 = 4k + 4

8k – 4k = 4 – 2

4k = 2

k = 2/4

= 1/2

Now, let us substitute the values, and we get

= 6

∴ The coordinates of the required point are (4, -2, 6).

6. If A and B be the points (3, 4, 5) and (–1, 3, –7), respectively, find the equation of the set of points P such that PA2 + PB2 = k2, where k is a constant.

Solution:

Given:

Points A (3, 4, 5) and B (-1, 3, -7)

x1 = 3, y1 = 4, z1 = 5;

x2 = -1, y2 = 3, z2 = -7;

PA2 + PB2 = k2 ……….(1)

Let the point be P (x, y, z).

Now, by using the distance formula,

We know that the distance between two points P (x1, y1, z1) and Q (x2, y2, z2) is given by

So,

And

Now, substituting these values in (1), we have

[(3 – x)2 + (4 – y)2 + (5 – z)2] + [(-1 – x)2 + (3 – y)2 + (-7 – z)2] = k2

[(9 + x2 – 6x) + (16 + y2 – 8y) + (25 + z2 – 10z)] + [(1 + x2 + 2x) + (9 + y2 – 6y) + (49 + z2 + 14z)] = k2

9 + x2 – 6x + 16 + y2 – 8y + 25 + z2 – 10z + 1 + x2 + 2x + 9 + y2 – 6y + 49 + z2 + 14z = k2

2×2 + 2y2 + 2z2 – 4x – 14y + 4z + 109 = k2

2×2 + 2y2 + 2z2 – 4x – 14y + 4z = k2 – 109

2 (x2 + y2 + z2 – 2x – 7y + 2z) = k2 – 109

(x2 + y2 + z2 – 2x – 7y + 2z) = (k2 – 109)/2

Hence, the required equation is (x2 + y2 + z2 – 2x – 7y + 2z) = (k2 – 109)/2.