NCERT Solutions Class 11 Maths Chapter 12 Limits and Derivatives
Limits and Derivatives NCERT Solutions for Class 11
SimplyAcad is providing you with solutions that cover all the questions prescribed in your NCERT maths textbook. NCERT Solutions for Class 11 Maths Chapter 12 Limits and Derivatives is one of the most vital chapters in the syllabus and students must make consistent practice to score well in their examination.
Limits and Derivatives NCERT Solutions are prepared by subject matter experts for students to get their basics strong. The solutions for all the exercises are solved below in an understandable and organised way for ease of students. These answers are in accordance with the most recent syllabus of the syllabus 2024-25, scroll below to find them.

NCERT Solutions for Class 11 Maths Chapter 12 Limits and Derivatives Exercise 12.1
1. Evaluate the given limit:
Solution:
Given,
![]()
Substituting x = 3, we get
= 3 + 3
= 6
2. Evaluate the given limit:
Solution:
Given limit,
Substituting x = π, we get
= (π – 22 / 7)
3. Evaluate the given limit:
Solution:
Given limit,
Substituting r = 1, we get
= π(1)2
= π
4. Evaluate the given limit:![]()
Solution:
Given limit,
![]()
Substituting x = 4, we get
![]() = [4(4) + 3] / (4 – 2)
= [4(4) + 3] / (4 – 2)
= (16 + 3) / 2
= 19 / 2
5. Evaluate the given limit:
Solution:
Given limit,
Substituting x = -1, we get
= [(-1)10 + (-1)5 + 1] / (-1 – 1)
= (1 – 1 + 1) / – 2
= – 1 / 2
6. Evaluate the given limit:
Solution:
Given limit,
= [(0 + 1)5 – 1] / 0
=0
Since this limit is undefined,
Substitute x + 1 = y, then x = y – 1

7. Evaluate the given limit:
Solution:

8. Evaluate the given limit:
Solution:

9. Evaluate the given limit:![]()
Solution:
= [a (0) + b] / c (0) + 1
= b / 1
= b
10. Evaluate the given limit:
Solution:
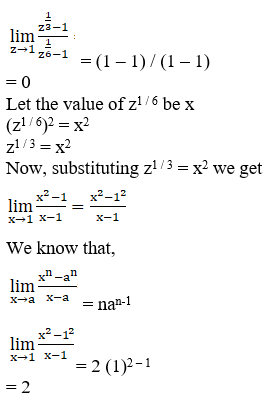
11. Evaluate the given limit:
Solution:
Given limit,
Substituting x = 1,
= [a (1)2 + b (1) + c] / [c (1)2 + b (1) + a]
= (a + b + c) / (a + b + c)
Given,
= 1
12. Evaluate the given limit:
Solution:
By substituting x = – 2, we get
13. Evaluate the given limit:
Solution:
Given

14. Evaluate the given limit:
Solution:

15. Evaluate the given limit:
Solution:

16. Evaluate the given limit:
Solution:
17. Evaluate the given limit:
Solution:

18. Evaluate the given limit:
Solution:

19. Evaluate the given limit:
Solution:
20. Evaluate the given limit:
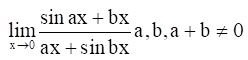
Solution:

21. Evaluate the given limit:
Solution:
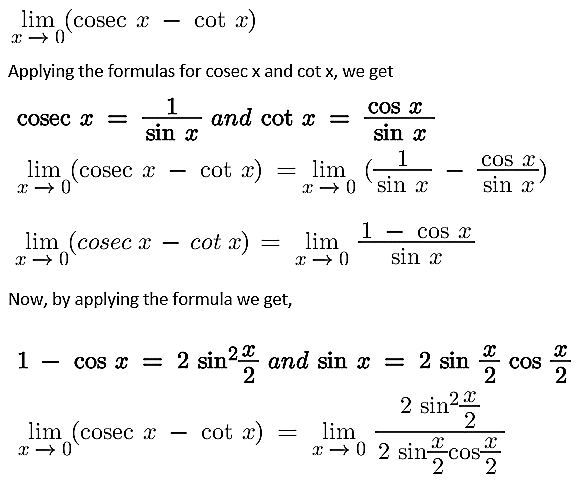

22. Evaluate the given limit:
Solution:


23.

Solution:



24. Find

Solution:


25. Evaluate
, where f(x) =
Solution:



26. Find
, where f (x) =
Solution:


27. Find
, where
Solution:


28. Suppose

what are the possible values of a and b?
Solution:


29. Let a1, a2,………an be fixed real numbers and define a function
f (x) = (x – a1) (x – a2) ……. (x – an).
What is
For some a ≠ a1, a2, ……. an, compute
.
Solution:


30. If 
exist?
Solution:

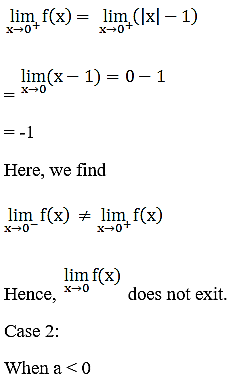

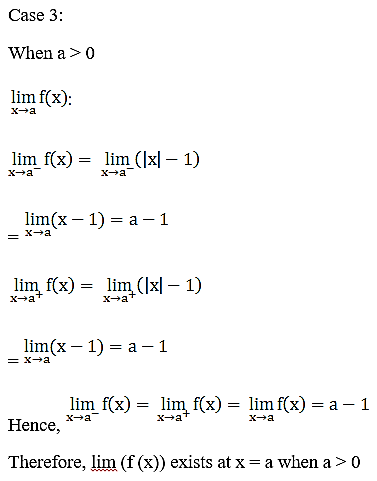
31. If the function f(x) satisfies 
Solution:

32. If  For what integers m and n does both
For what integers m and n does both and
exist?
Solution:



NCERT Solutions for Class 11 Maths Chapter 12 Limits and Derivatives Exercise 12.2
1. Find the derivative of x2– 2 at x = 10.
Solution:
Let f (x) = x2 – 2

2. Find the derivative of x at x = 1.
Solution:
Let f (x) = x
Then,


3. Find the derivative of 99x at x = l00.
Solution:
Let f (x) = 99x,
From the first principle,

= 99
4. Find the derivative of the following functions from the first principle.
(i) x3 – 27
(ii) (x – 1) (x – 2)
(iii) 1 / x2
(iv) x + 1 / x – 1
Solution:
(i) Let f (x) = x3 – 27
From the first principle,

(ii) Let f (x) = (x – 1) (x – 2)
From the first principle,

(iii) Let f (x) = 1 / x2
From the first principle, we get

(iv) Let f (x) = x + 1 / x – 1
From the first principle, we get


5. For the function  , prove that f’ (1) =100 f’ (0).
, prove that f’ (1) =100 f’ (0).
Solution:

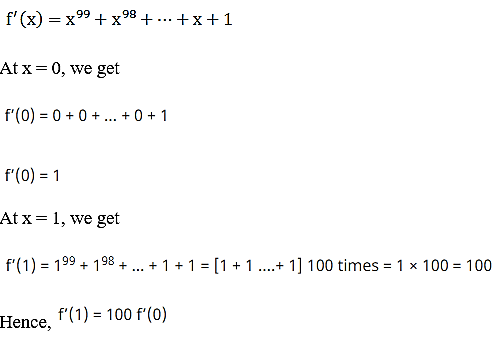
6. Find the derivative of ![]() for some fixed real number a.
for some fixed real number a.
Solution:

7. For some constants a and b, find the derivative of
(i) (x − a) (x − b)
(ii) (ax2 + b)2
(iii) x – a / x – b
Solution:
(i) (x – a) (x – b)

(ii) (ax2 + b)2

= 4ax (ax2 + b)
(iii) x – a / x – b



8. Find the derivative of 
Solution:

9. Find the derivative of
(i) 2x – 3 / 4
(ii) (5×3 + 3x – 1) (x – 1)
(iii) x-3 (5 + 3x)
(iv) x5 (3 – 6x-9)
(v) x-4 (3 – 4x-5)
(vi) (2 / x + 1) – x2 / 3x – 1
Solution:
(i)

(ii)

(iii)


(iv)

(v)

(vi)


10. Find the derivative of cos x from the first principle.
Solution:
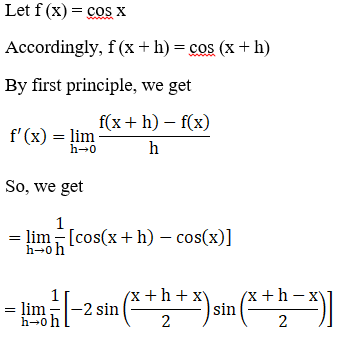
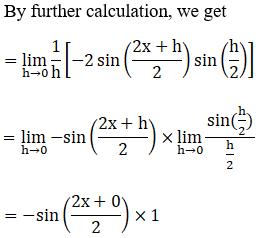
11. Find the derivative of the following functions.
(i) sin x cos x
(ii) sec x
(iii) 5 sec x + 4 cos x
(iv) cosec x
(v) 3 cot x + 5 cosec x
(vi) 5 sin x – 6 cos x + 7
(vii) 2 tan x – 7 sec x
Solution:
(i) sin x cos x


(ii) sec x
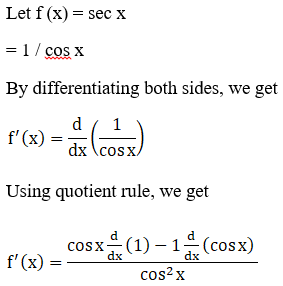
![]()
(iii) 5 sec x + 4 cos x

(iv) cosec x

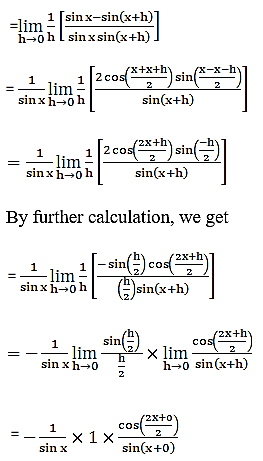
(v) 3 cot x + 5 cosec x



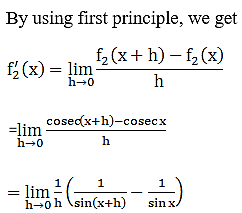
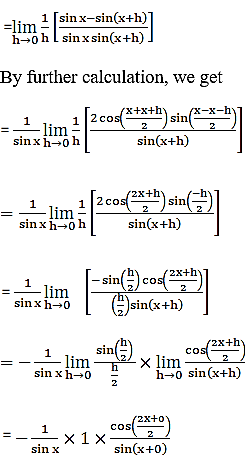


(vi)5 sin x – 6 cos x + 7
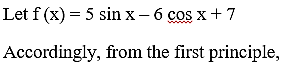

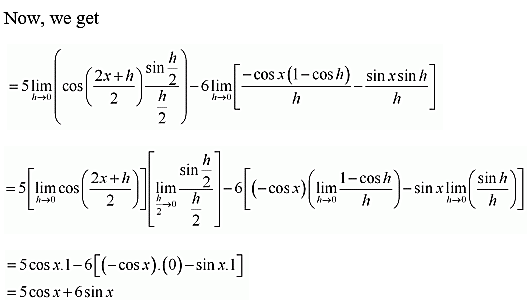
(vii) 2 tan x – 7 sec x




NCERT Solutions for Class 11 Maths Chapter 12 Limits and Derivatives Miscellaneous exercise
1. Find the derivative of the following functions from the first principle.
(i) –x
(ii) (–x)–1
(iii) sin (x + 1)
(iv)
Solution:

(ii) (-x)-1
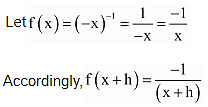
![]()

= 1 / x2
(iii) sin (x + 1)
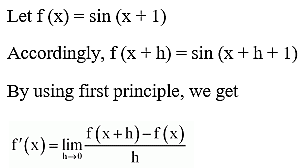


(iv)

We get,


Find the derivative of the following functions. (It is to be understood that a, b, c, d, p, q, r and s are fixed non-zero constants, and m and n are integers.)
2. (x + a)
Solution:

3. (px + q) (r / x + s)
Solution:


4. (ax + b) (cx + d)2
Solution:
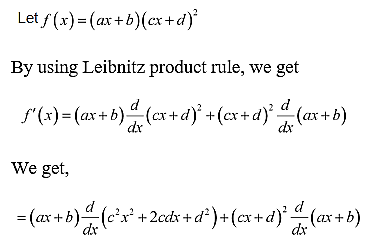

5. (ax + b) / (cx + d)
Solution:


6. (1 + 1 / x) / (1 – 1 / x)
Solution:


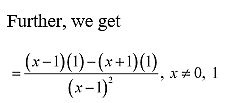
7. 1 / (ax2 + bx + c)
Solution:
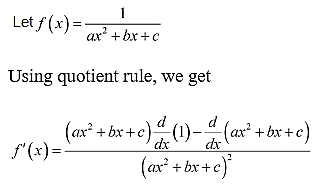

8. (ax + b) / px2 + qx + r
Solution:
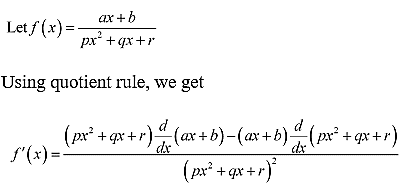

9. (px2 + qx + r) / ax + b
Solution:
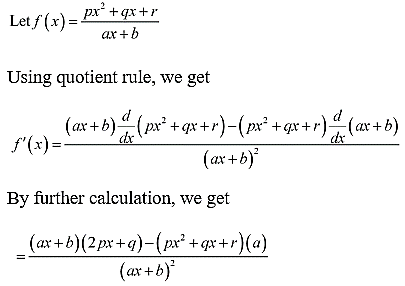
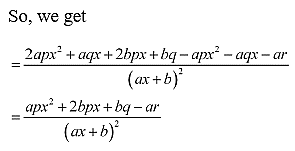
10. (a / x4) – (b / x2) + cos x
Solution:


11.
Solution:

12. (ax + b)n
Solution:
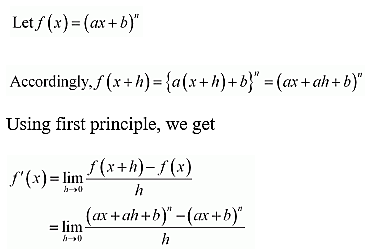

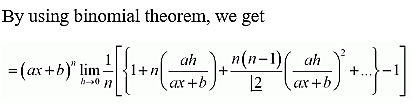


13. (ax + b)n (cx + d)m
Solution:





14. sin (x + a)
Solution:



15. cosec x cot x
Solution:

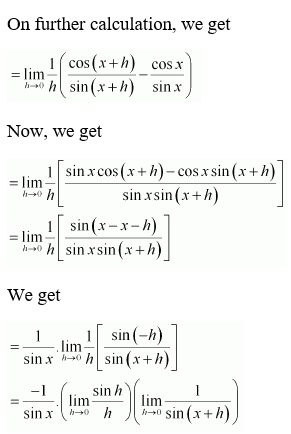
So, we get




16.
Solution:

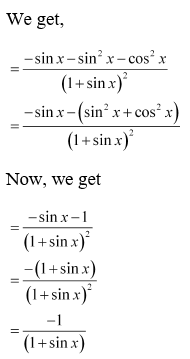
17.
Solution:


18.
Solution:



19. sinn x
Solution:




20.
Solution:


21.
Solution:




22. x4 (5 sin x – 3 cos x)
Solution:


23. (x2 + 1) cos x
Solution:

24. (ax2 + sin x) (p + q cos x)
Solution:

25.
Solution:
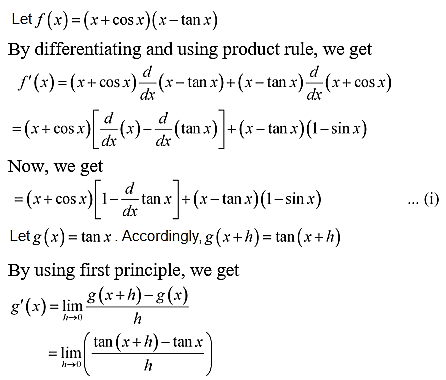

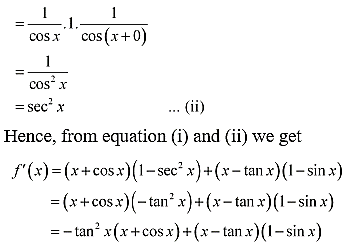
26.
Solution:


27.
Solution:

28.
Solution:
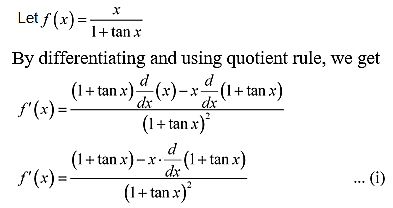


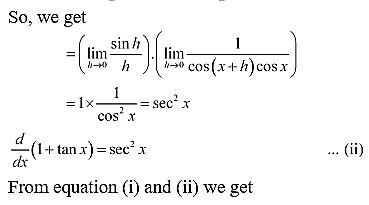

29. (x + sec x) (x – tan x)
Solution:












30.
Solution:

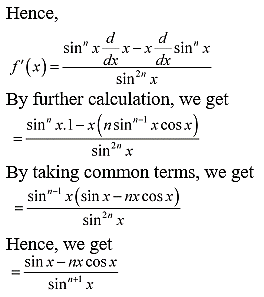
latest video
news via inbox
Nulla turp dis cursus. Integer liberos euismod pretium faucibua











































