NCERT Solutions Class 11 Maths Chapter 3 Trigonometric Functions
NCERT Solutions for Class 11 Maths Chapter 3 – Trigonometric Functions
NCERT Solutions For Class 11 Maths Chapter 3 Trigonometric Functions has many formulas and theorems Hence we have designed the steps by steps method to solve all the questions. NCERT Solutions for Class 11 Maths Chapter 3 are comprehensive format and highly reliable to enhance problem-solving skills to score more marks in the examination. Trigonometry is an important part of Class 11 Maths that involves studying various relations between sides and angles of triangles.
This chapter contains 3 exercises along with a miscellaneous exercise.

These solutions are helpful for the students to get an idea of how to answer the questions from the board exam perspective
NCERT Solutions For Class 11 Maths Chapter 3 Trigonometric Functions Exercise 3.1
The Exercice 3.1 chapter contains questions revolving around Trigonometric functions.
- Introduction
- Angles
- Degree measure
- Radian measure
- Relation between radian and real numbers
- Relation between degree and radian

1. Find the radian measures corresponding to the following degree measures:
(i) 25° (ii) – 47° 30′ (iii) 240° (iv) 520°
Solution:

(iv) 520°
2. Find the degree measures corresponding to the following radian measures (Use π = 22/7).
(i) 11/16
(ii) -4
(iii) 5π/3
(iv) 7π/6
Solution:
(i) 11/16
Here, π radian = 180°
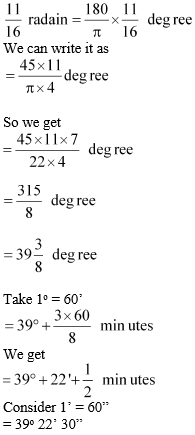
(ii) -4
Here, π radian = 180°

(iii) 5π/3
Here, π radian = 180°
We get
= 300o
(iv) 7π/6
Here, π radian = 180°
We get
= 210o
3. A wheel makes 360 revolutions in one minute. Through how many radians does it turn in one second?
Solution:
It is given that
No. of revolutions made by the wheel in
1 minute = 360
1 second = 360/60 = 6
We know that
The wheel turns an angle of 2π radian in one complete revolution.
In 6 complete revolutions, it will turn an angle of 6 × 2π radian = 12 π radian
Therefore, in one second, the wheel turns at an angle of 12π radian.
4. Find the degree measure of the angle subtended at the centre of a circle of radius 100 cm by an arc of length 22 cm (Use π = 22/7).
Solution:

5. In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of the minor arc of the chord.
Solution:
The dimensions of the circle are
Diameter = 40 cm
Radius = 40/2 = 20 cm
Consider AB as the chord of the circle, i.e., length = 20 cm
In ΔOAB,
Radius of circle = OA = OB = 20 cm
Similarly AB = 20 cm
Hence, ΔOAB is an equilateral triangle.
θ = 60° = π/3 radian
In a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre,
We get θ = 1/r
Therefore, the length of the minor arc of the chord is 20π/3 cm.
6. If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii.
Solution:

7. Find the angle in the radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm (ii) 15 cm (iii) 21 cm
Solution:
In a circle of radius r unit, if an arc of length l unit subtends an angle θ radian at the centre, then θ = 1/r
We know that r = 75 cm
(i) l = 10 cm
So we get
θ = 10/75 radian
By further simplification,
θ = 2/15 radian
(ii) l = 15 cm
So, we get
θ = 15/75 radian
By further simplification,
θ = 1/5 radian
(iii) l = 21 cm
So, we get
θ = 21/75 radian
By further simplification,
θ = 7/25 radian
NCERT Solutions For Class 11 Maths Chapter 3 Trigonometric Functions Exercise 3.2

Prove that:
1.
Solution:

2.
![]()
Solution:
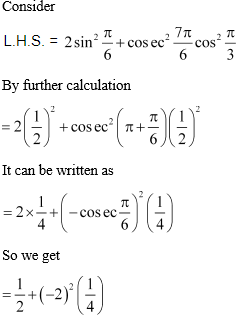
Here
= 1/2 + 4/4
= 1/2 + 1
= 3/2
= RHS
3.
Solution:
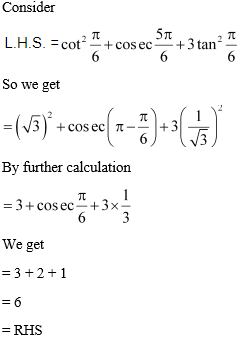
4.
![]()
Solution:
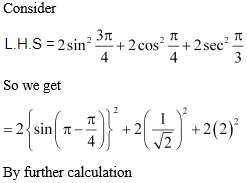
5. Find the value of:
(i) sin 75o
(ii) tan 15o
Solution:

(ii) tan 15°
It can be written as
= tan (45° – 30°)
Using formula
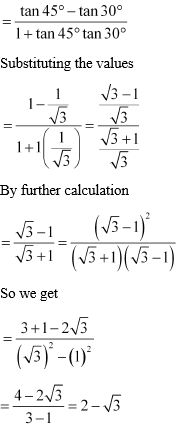
Prove the following:
6.
![]()
Solution:


7.
Solution:

8.

Solution:
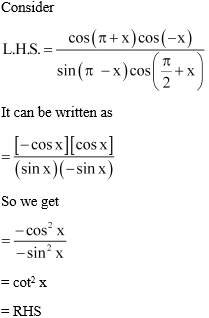
9.
![]()
Solution:
Consider
![]()
It can be written as
= sin x cos x (tan x + cot x)
So we get

10. sin (n + 1)x sin (n + 2)x + cos (n + 1)x cos (n + 2)x = cos x
Solution:
LHS = sin (n + 1)x sin (n + 2)x + cos (n + 1)x cos (n + 2)x

11.
![]()
Solution:
Consider
![]()
Using the formula

12. sin2 6x – sin2 4x = sin 2x sin 10x
Solution:


13. cos2 2x – cos2 6x = sin 4x sin 8x
Solution:

We get
= [2 cos 4x cos (-2x)] [-2 sin 4x sin (-2x)]
It can be written as
= [2 cos 4x cos 2x] [–2 sin 4x (–sin 2x)]
So we get
= (2 sin 4x cos 4x) (2 sin 2x cos 2x)
= sin 8x sin 4x
= RHS
14. sin 2x + 2sin 4x + sin 6x = 4cos2 x sin 4x
Solution:

By further simplification
= 2 sin 4x cos (– 2x) + 2 sin 4x
It can be written as
= 2 sin 4x cos 2x + 2 sin 4x
Taking common terms
= 2 sin 4x (cos 2x + 1)
Using the formula
= 2 sin 4x (2 cos2 x – 1 + 1)
We get
= 2 sin 4x (2 cos2 x)
= 4cos2 x sin 4x
= R.H.S.
15. cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)
Solution:
Consider
LHS = cot 4x (sin 5x + sin 3x)
It can be written as
![]()
Using the formula

= 2 cos 4x cos x
Hence, LHS = RHS.
16.
Solution:
Consider
![]()
Using the formula
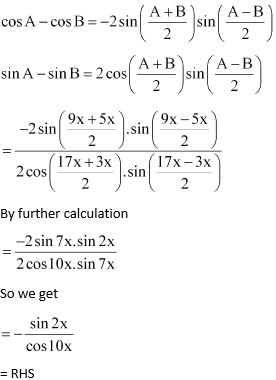
17.
![]()
Solution:

18.
Solution:

19.
Solution:

20.
![]()
Solution:

21.
![]()
Solution:

22. cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1
Solution:

23.
![]()
Solution:
Consider
LHS = tan 4x = tan 2(2x)
By using the formula

24. cos 4x = 1 – 8sin2 x cos2 x
Solution:
Consider
LHS = cos 4x
We can write it as
= cos 2(2x)
Using the formula cos 2A = 1 – 2 sin2 A
= 1 – 2 sin2 2x
Again by using the formula sin2A = 2sin A cos A
= 1 – 2(2 sin x cos x) 2
So we get
= 1 – 8 sin2x cos2x
= R.H.S.
25. cos 6x = 32 cos6 x – 48 cos4 x + 18 cos2 x – 1
Solution:
Consider
L.H.S. = cos 6x
It can be written as
= cos 3(2x)
Using the formula cos 3A = 4 cos3 A – 3 cos A
= 4 cos3 2x – 3 cos 2x
Again by using formula cos 2x = 2 cos2 x – 1
= 4 [(2 cos2 x – 1)3 – 3 (2 cos2 x – 1)
By further simplification
= 4 [(2 cos2 x) 3 – (1)3 – 3 (2 cos2 x) 2 + 3 (2 cos2 x)] – 6cos2 x + 3
We get
= 4 [8cos6x – 1 – 12 cos4x + 6 cos2x] – 6 cos2x + 3
By multiplication
= 32 cos6x – 4 – 48 cos4x + 24 cos2 x – 6 cos2x + 3
On further calculation
= 32 cos6x – 48 cos4x + 18 cos2x – 1
= R.H.S.
NCERT Solutions For Class 11 Maths Chapter 3 Trigonometric Functions Exercise 3.4
The Exercice 3.4 chapter contains questions revolving around trigonometric equations. Equations involving trigonometric functions of a variable are called trigonometric equations.

1. tan x = √3
Solution:

2. sec x = 2
Solution:

3. cot x = – √3
Solution:


4. cosec x = – 2
Solution:
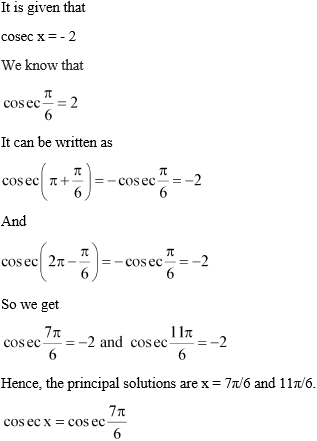

Find the general solution for each of the following equations:
5. cos 4x = cos 2x
Solution:

6. cos 3x + cos x – cos 2x = 0
Solution:

7. sin 2x + cos x = 0
Solution:
It is given that
sin 2x + cos x = 0
We can write it as
2 sin x cos x + cos x = 0
cos x (2 sin x + 1) = 0
cos x = 0 or 2 sin x + 1 = 0
Let cos x = 0

8. sec2 2x = 1 – tan 2x
Solution:
It is given that
sec2 2x = 1 – tan 2x
We can write it as
1 + tan2 2x = 1 – tan 2x
tan2 2x + tan 2x = 0
Taking common terms
tan 2x (tan 2x + 1) = 0
Here
tan 2x = 0 or tan 2x + 1 = 0
If tan 2x = 0
tan 2x = tan 0
We get
2x = nπ + 0, where n ∈ Z
x = nπ/2, where n ∈ Z
tan 2x + 1 = 0
We can write it as
tan 2x = – 1
So we get
Here
2x = nπ + 3π/4, where n ∈ Z
x = nπ/2 + 3π/8, where n ∈ Z
Hence, the general solution is nπ/2 or nπ/2 + 3π/8, n ∈ Z.
9. sin x + sin 3x + sin 5x = 0
Solution:
It is given that
sin x + sin 3x + sin 5x = 0
We can write it as
(sin x + sin 5x) + sin 3x = 0
Using the formula
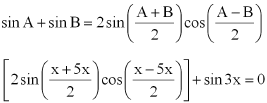
By further calculation
2 sin 3x cos (-2x) + sin 3x = 0
It can be written as
2 sin 3x cos 2x + sin 3x = 0
By taking out the common terms
sin 3x (2 cos 2x + 1) = 0
Here
sin 3x = 0 or 2 cos 2x + 1 = 0
If sin 3x = 0
3x = nπ, where n ∈ Z
We get
x = nπ/3, where n ∈ Z
If 2 cos 2x + 1 = 0
cos 2x = – 1/2
By further simplification
= – cos π/3
= cos (π – π/3)
So we get
cos 2x = cos 2π/3
Here
NCERT Solutions For Class 11 Maths Chapter 3 Trigonometric Functions Exercise : Miscellaneous

Prove that:
1.
![]()
Solution:


We get
= 0
= RHS
2. (sin 3x + sin x) sin x + (cos 3x – cos x) cos x = 0
Solution:
Consider
LHS = (sin 3x + sin x) sin x + (cos 3x – cos x) cos x
By further calculation,
= sin 3x sin x + sin2 x + cos 3x cos x – cos2 x
Taking out the common terms,
= cos 3x cos x + sin 3x sin x – (cos2 x – sin2 x)
Using the formula
cos (A – B) = cos A cos B + sin A sin B
= cos (3x – x) – cos 2x
So, we get
= cos 2x – cos 2x
= 0
= RHS
3.
![]()
Solution:
Consider
LHS = (cos x + cos y) 2 + (sin x – sin y) 2
By expanding using the formula, we get
= cos2 x + cos2 y + 2 cos x cos y + sin2 x + sin2 y – 2 sin x sin y
Grouping the terms,
= (cos2 x + sin2 x) + (cos2 y + sin2 y) + 2 (cos x cos y – sin x sin y)
Using the formula cos (A + B) = (cos A cos B – sin A sin B)
= 1 + 1 + 2 cos (x + y)
By further calculation,
= 2 + 2 cos (x + y)
Taking 2 as common
= 2 [1 + cos (x + y)]
From the formula cos 2A = 2 cos2 A – 1
4.
![]()
Solution:
LHS = (cos x – cos y) 2 + (sin x – sin y) 2
By expanding using the formula,
= cos2 x + cos2 y – 2 cos x cos y + sin2 x + sin2 y – 2 sin x sin y
Grouping the terms,
= (cos2 x + sin2 x) + (cos2 y + sin2 y) – 2 (cos x cos y + sin x sin y)
Using the formula cos (A – B) = cos A cos B + sin A sin B
= 1 + 1 – 2 [cos (x – y)]
By further calculation,
= 2 [1 – cos (x – y)]
From formula cos 2A = 1 – 2 sin2 A
5. sin x + sin 3x + sin 5x + sin 7x = 4 cos x cos 2x sin 4x
Solution:


6.
![]()
Solution:

7.
![]()
Solution:


8. Find sin x/2, cos x/2 and tan x/2 in each of the following.
![]()
Solution:

cos x = -3/5
From the formula,


9. cos x = -1/3, x in quadrant III
Solution:


10. sin x = 1/4, x in quadrant II
Solution:

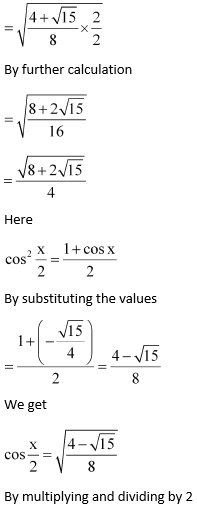
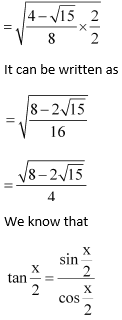

latest video
news via inbox
Nulla turp dis cursus. Integer liberos euismod pretium faucibua
























