NCERT Solutions for Class 11 Maths Chapter 6 Permutations And Combinations

NCERT Solutions for Class 11 Maths Chapter 6 Permutations and Combinations are prepared by SimplyAcad experts. The solutions are designed to have a better understanding of the topic and to score better marks in the exam. We continuously update the content as soon as we receive any notification from CBSE or NCERT.

NCERT Solutions for Class 11 Chapter 6 Permutations and Combinations – Exercise 6.1

NCERT Solutions for Class 11 Maths Chapter 6 – Permutations and Combinations Exercise 6.1 contains following topics:

1. Introduction to Permutations and Combinations
2. Fundamental Principle of Counting

1. How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5, assuming that

(i) Repetition of the digits is allowed?

(ii) Repetition of the digits is not allowed?

Solution:

(i) Let the 3-digit number be ABC, where C is at the units place, B at the tens place and A at the hundreds place.

Now, when repetition is allowed,

The number of digits possible at C is 5. As repetition is allowed, the number of digits possible at B and A is also 5 at each.

Hence, the total number possible 3-digit numbers =5 × 5 × 5 =125

(ii) Let the 3-digit number be ABC, where C is at the units place, B at the tens place and A at the hundreds place.

Now, when repetition is not allowed,

The number of digits possible at C is 5. Let’s suppose one of 5 digits occupies place C; now, as the repletion is not allowed, the possible digits for place B are 4, and similarly, there are only 3 possible digits for place A.

Therefore, the total number of possible 3-digit numbers=5 × 4 × 3=60

2. How many 3-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?

Solution:

Let the 3-digit number be ABC, where C is at the unit’s place, B at the tens place and A at the hundreds place.

As the number has to be even, the digits possible at C are 2 or 4 or 6. That is, the number of possible digits at C is 3.

Now, as repetition is allowed, the digits possible at B is 6. Similarly, at A, also, the number of digits possible is 6.

Therefore, the total number of possible 3-digit numbers = 6 × 6 × 3 = 108

3. How many 4-letter codes can be formed using the first 10 letters of the English alphabet, if no letter can be repeated?

Solution:

Let the 4-digit code be 1234.

In the first place, the number of letters possible is 10.

Let’s suppose any 1 of the ten occupies place 1.

Now, as repetition is not allowed, the number of letters possible at place 2 is 9. Now, at 1 and 2, any 2 of the 10 alphabets have been taken. The number of alphabets left for place 3 is 8, and similarly, the number of alphabets possible at 4 is 7.

Therefore, the total number of 4-digit codes=10 × 9 × 8 × 7=5040

4. How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?

Solution:

Let the five-digit number be ABCDE. Given that the first 2 digits of each number are 67. Therefore, the number is 67CDE.

As repetition is not allowed and 6 and 7 are already taken, the digits available for place C are 0,1,2,3,4,5,8,9. The number of possible digits at place C is 8. Suppose one of them is taken at C; now, the digits possible at place D is 7. And similarly, at E, the possible digits are 6.

∴ The total five-digit numbers with given conditions = 8 × 7 × 6 = 336

5. A coin is tossed 3 times, and the outcomes are recorded. How many possible outcomes are there?

Solution:

Given, A coin is tossed 3 times, and the outcomes are recorded.

The possible outcomes after a coin toss are head and tail.

The number of possible outcomes at each coin toss is 2.

∴ The total number of possible outcomes after 3 times = 2 × 2 × 2 = 8

6. Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?

Solution:

Given, 5 flags of different colours.

We know the signal requires 2 flags.

The number of flags possible for the upper flag is 5.

Now, as one of the flags is taken, the number of flags remaining for the lower flag in the signal is 4.

The number of ways in which signal can be given = 5 × 4 = 20

NCERT Solutions for Class 11 Chapter 6 Permutations and Combinations – Exercise 6.2

NCERT Solutions for Class 11 Maths Chapter 6 – Permutations and Combinations Exercise 6.2 contains following topics:

1. Permutations
   1. Permutations when all the objects are distinct
   2. Factorial notation

1. Evaluate
(i) 8!

(ii) 4! – 3!

Solution:

(i) Consider 8!

We know that 8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1

= 40320

(ii) Consider 4!-3!

4!-3! = (4 × 3!) – 3!

Above equation can be written as

= 3! (4-1)

= 3 × 2 × 1 × 3

= 18

2. Is 3! + 4! = 7!?

Solution:

Consider LHS 3! + 4!

Computing left hand side, we get

3! + 4! = (3 × 2 × 1) + (4 × 3 × 2 × 1)

= 6 + 24

= 30

Again considering RHS and computing, we get

7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040

Therefore LHS ≠ RHS

Therefore 3! + 4! ≠ 7!

3. Compute

Solution:

4. If find x.

Solution:

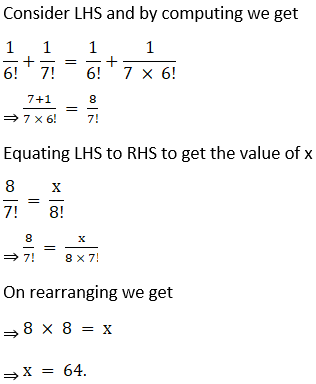
5. Evaluate

,

When
(i) n = 6, r = 2
(ii) n = 9, r = 5

Solution:

NCERT Solutions for Class 11 Chapter 6 Permutations and Combinations – Exercise 6.3

NCERT Solutions for Class 11 Maths Chapter 6 – Permutations and Combinations Exercise 6.3 contains following topics:

Permutations

Derivation of the formula for nPr

Permutations when all the objects are not distinct objects

1. How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated?

Solution:

2. How many 4-digit numbers are there with no digit repeated?

Solution:

To find the four-digit number (digits do not repeat)

Now, we will have 4 places where 4 digits are to be put.

So, at thousand’s place = There are 9 ways, as 0 cannot be at thousand’s place = 9 ways

At hundredth’s place = There are 9 digits to be filled, as 1 digit is already taken = 9 ways

At ten’s place = There are now 8 digits to be filled, as 2 digits are already taken = 8 ways

At unit’s place = There are 7 digits that can be filled = 7 ways

The total number of ways to fill the four places = 9 × 9 × 8 × 7 = 4536 ways

So, a total of 4536 four-digit numbers can be there with no digits repeated.

3. How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7, if no digit is repeated?

Solution:

An even number means that the last digit should be even.

Number of possible digits at one’s place = 3 (2, 4 and 6)

⇒ Number of permutations=

One of the digits is taken at one’s place; the number of possible digits available = 5

⇒ Number of permutations=

Therefore, the total number of permutations =3 × 20=60

4. Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, and 5 if no digit is repeated. How many of these will be even?

Solution:

Total number of digits possible for choosing = 5

Number of places for which a digit has to be taken = 4

As there is no repetition allowed,

⇒ Number of permutations =

The number will be even when 2 and 4 are in one’s place.

The possibility of (2, 4) at one’s place = 2/5 = 0.4

The total number of even numbers = 120 × 0.4 = 48

5. From a committee of 8 persons, in how many ways can we choose a chairman and a vice chairman, assuming one person cannot hold more than one position?

Solution:

Total number of people in committee = 8

Number of positions to be filled = 2

⇒ Number of permutations =

6. Find n if n-1P3: nP3 = 1: 9.

Solution:

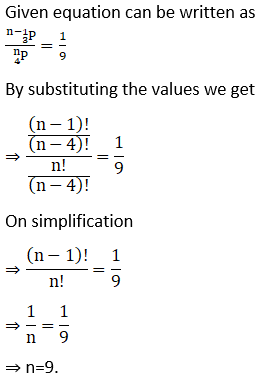
7. Find r if

(i)5Pr = 26Pr-1

(ii) 5Pr = 6Pr-1

Solution:

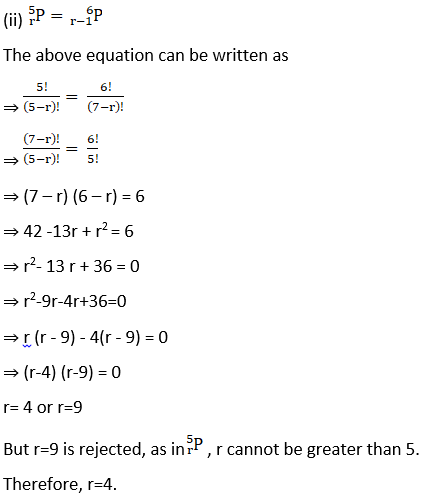
8. How many words, with or without meaning, can be formed using all the letters of the word EQUATION, using each letter exactly once?

Solution:

Total number of different letters in EQUATION = 8

Number of letters to be used to form a word = 8

⇒ Number of permutations =

9. How many words, with or without meaning, can be made from the letters of the word MONDAY, assuming that no letter is repeated, if
(i) 4 letters are used at a time

(ii) All letters are used at a time
(iii) all letters are used, but the first letter is a vowel

Solution:

(i) Number of letters to be used =4

⇒ Number of permutations =

(ii) Number of letters to be used = 6

⇒ Number of permutations =

(iii) Number of vowels in MONDAY = 2 (O and A)

⇒ Number of permutations in vowel =

Now, the remaining places = 5

Remaining letters to be used =5

⇒ Number of permutations =

Therefore, the total number of permutations = 2 × 120 =240

10. In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?

Solution:

Total number of letters in MISSISSIPPI = 11

Letter number of occurrence

M	1
I	4
S	4
P	2

⇒ Number of permutations =

We take that 4 I’s come together, and they are treated as 1 letter.

∴ Total number of letters=11 – 4 + 1 = 8

⇒ Number of permutations =

Therefore, the total number of permutations where four I’s don’t come together = 34650-840=33810

11. In how many ways can the letters of the word PERMUTATIONS be arranged if the

(i) Words start with P and end with S

(ii) Vowels are all together
(iii) There are always 4 letters between P and S

Solution:

(i) Total number of letters in PERMUTATIONS =12

The only repeated letter is T; 2times

The first and last letters of the word are fixed as P and S, respectively.

Number of letters remaining =12 – 2 = 10

⇒ Number of permutations =

(ii) Number of vowels in PERMUTATIONS = 5 (E, U, A, I, O)

Now, we consider all the vowels together as one.

Number of permutations of vowels = 120

Now total number of letters = 12 – 5 + 1= 8

⇒ Number of permutations =

Therefore, total number of permutations = 120 × 20160 = 2419200

(iii) Number of places is as 1 2 3 4 5 6 7 8 9 10 11 12

There should always be 4 letters between P and S.

Possible places of P and S are 1 and 6, 2 and 7, 3 and 8, 4 and 9, 5 and 10, 6 and 11, 7 and 12

Possible ways =7

Also, P and S can be interchanged.

No. of permutations =2 × 7 =14

The remaining 10 places can be filled with 10 remaining letters,

∴ No. of permutations =

Therefore, the total number of permutations = 14 × 1814400 =25401600

NCERT Solutions for Class 11 Chapter 6 Permutations and Combinations – Exercise 6.4

NCERT Solutions for Class 11 Maths Chapter 6 – Permutations and Combinations Exercise 6.4 contains following topics:

1. Combination

1. If nC8 = nC2, find nC2.

Solution:

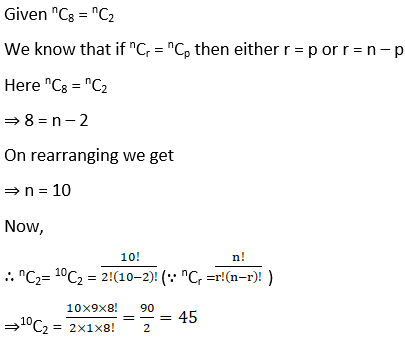
2. Determine n if
(i) 2nC3: nC3 = 12: 1
(ii) 2nC3: nC3 = 11: 1

Solution:

Simplifying and computing,

⇒ 4 × (2n – 1) = 12 × (n – 2)

⇒ 8n – 4 = 12n – 24

⇒ 12n – 8n = 24 – 4

⇒ 4n = 20

∴ n = 5

⇒ 11n – 8n = 22 – 4

⇒ 3n = 18

∴ n = 6

3. How many chords can be drawn through 21 points on a circle?

Solution:

Given, 21 points on a circle.

We know that we require two points on the circle to draw a chord.

∴ The number of chords is

⇒ 21C2=

∴ The total number of chords that can be drawn is 210.

4. In how many ways can a team of 3 boys and 3 girls be selected from 5 boys and 4 girls?

Solution:

Given, 5 boys and 4 girls are in total.

We can select 3 boys from 5 boys in 5C3 ways.

Similarly, we can select 3 boys from 54 girls in 4C3 ways.

∴ The number of ways a team of 3 boys and 3 girls can be selected is 5C3 × 4C3

⇒ 5C3 × 4C3 =

⇒ 5C3 × 4C3 = 10 × 4 = 40

∴ The number of ways a team of 3 boys and 3 girls can be selected is 5C3 × 4C3 = 40 ways

5. Find the number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour.

Solution:

Given, 6 red balls, 5 white balls and 5 blue balls.

We can select 3 red balls from 6 red balls in 6C3 ways.

Similarly, we can select 3 white balls from 5 white balls in 5C3 ways.

Similarly, we can select 3 blue balls from 5 blue balls in 5C3 ways.

∴ The number of ways of selecting 9 balls is 6C3 ×5C3 × 5C3

∴ The number of ways of selecting 9 balls from 6 red balls, 5 white balls and 5 blue balls if each selection consists of 3 balls of each colour is 6C3 ×5C3 × 5C3 = 2000

6. Determine the number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination.

Solution:

Given, a deck of 52 cards.

There are 4 Ace cards in a deck of 52 cards.

According to the question, we need to select 1 Ace card out of the 4 Ace cards.

∴ The number of ways to select 1 Ace from 4 Ace cards is 4C1

⇒ More 4 cards are to be selected now from 48 cards (52 cards – 4 Ace cards)

∴ The number of ways to select 4 cards from 48 cards is 48C4

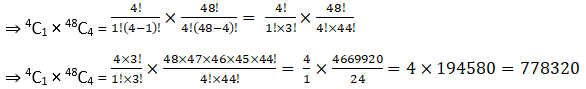
∴ The number of 5 card combinations out of a deck of 52 cards if there is exactly one ace in each combination is 778320.

7. In how many ways can one select a cricket team of eleven from 17 players in which only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers?

Solution:

Given, 17 players, in which, only 5 players can bowl if each cricket team of 11 must include exactly 4 bowlers.

There are 5 players to bowl, and we can include 4 bowlers in a team of 11.

∴ The number of ways in which bowlers can be selected is 5C4

Now, other players left are = 17 – 5(bowlers) = 12

Since we need 11 players in a team and 4 bowlers have already been selected, we need to select 7 more players from 12.

∴ The number of ways we can select these players is 12C7

∴ The total number of combinations possible is 5C4 × 12C7

∴ The number of ways we can select a team of 11 players where 4 players are bowlers from 17 players is 3960.

8. A bag contains 5 black and 6 red balls. Determine the number of ways in which 2 black and 3 red balls can be selected.

Solution:

Given, a bag contains 5 black and 6 red balls.

The number of ways we can select 2 black balls from 5 black balls is 5C2

The number of ways we can select 3 red balls from 6 red balls is 6C3

The number of ways 2 black and 3 red balls can be selected is 5C2× 6C3

∴ The number of ways in which 2 black and 3 red balls can be selected from 5 black and 6 red balls is 200.

9. In how many ways can a student choose a programme of 5 courses if 9 courses are available and 2 specific courses are compulsory for every student?

Solution:

Given, 9 courses are available, and 2 specific courses are compulsory for every student.

Here, 2 courses are compulsory out of 9 courses, so a student needs to select 5 – 2 = 3 courses

∴ The number of ways in which 3 ways can be selected from 9 – 2(compulsory courses) = 7 is 7C3

∴ The number of ways a student selects 5 courses from 9 courses where 2 specific courses are compulsory is 35.

NCERT Solutions for Class 11 Chapter 6 Permutations and Combinations – Miscellaneous Exercise

1. How many words, with or without meaning, each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER?

Solution:

The word DAUGHTER has 3 vowels, A, E, U and 5 consonants D, G, H, T and R.

The three vowels can be chosen in 3C2, as only two vowels are to be chosen.

Similarly, the five consonants can be chosen in 5C3 ways.

∴ The number of choosing 2 vowels and 5 consonants would be 3C2 ×5C3

= 30

∴ The total number of ways is 30.

Each of these 5 letters can be arranged in 5 ways to form different words = 5P5

The total number of words formed would be = 30 × 120 = 3600

2. How many words, with or without meaning, can be formed using all the letters of the word EQUATION at a time so that the vowels and consonants occur together?

Solution:

In the word EQUATION, there are 5 vowels (A, E, I, O, U) and 3 consonants (Q, T, N)

The numbers of ways in which 5 vowels can be arranged are 5C5

…………… (i)

Similarly, the numbers of ways in which 3 consonants can be arranged are 3P3

…………….. (ii)

There are two ways in which vowels and consonants can appear together:

(AEIOU) (QTN) or (QTN) (AEIOU)

∴ The total number of ways in which vowel and consonant can appear together are 2 × 5C5 × 3C3

∴ 2 × 120 × 6 = 1440

3. A committee of 7 has to be formed from 9 boys and 4 girls. In how many ways can this be done when the committee consists of:
(i) Exactly 3 girls?

(ii) At least 3 girls?

(iii) At most 3 girls?

Solution:

(i) Given, exactly 3 girls.

The total numbers of girls are 4.

Out of which, 3 are to be chosen.

∴ The number of ways in which choice would be made = 4C3

The number of boys is 9, out of which 4 are to be chosen, which is given by 9C4

Total ways of forming the committee with exactly three girls

= 4C3 × 9C4

=

(ii) Given, at least 3 girls.

There are two possibilities for making a committee choosing at least 3 girls.

There are 3 girls and 4 boys, or there are 4 girls and 3 boys.

Choosing three girls we have done in (I).

Choosing four girls and 3 boys would be done in 4C4 ways.

And choosing 3 boys would be done in 9C3

Total ways = 4C4 ×9C3

The total number of ways of making the committee are

504 + 84 = 588

(iii) Given, at most 3 girls.

In this case, the numbers of possibilities are

0 girls and 7 boys

1 girl and 6 boys

2 girls and 5 boys

3 girls and 4 boys

The number of ways to choose 0 girls and 7 boys = 4C0 × 9C7

The number of choosing 3 girls and 4 boys is done in (1)

= 504

The total number of ways in which a committee can have at most 3 girls are = 36 + 336 + 756 + 504 = 1632

4. If the different permutations of all the letters of the word EXAMINATION are listed as in a dictionary, how many words are there in this list before the first word starting with E?

Solution:

In a dictionary, words are listed alphabetically, so to find the words,

Listed before E should start with the letter either A, B, C or D.

But the word EXAMINATION doesn’t have B, C or D.

Hence, the words should start with the letter A.

The remaining 10 places are to be filled by the remaining letters of the word EXAMINATION, which are E, X, A, M, 2N, T, 2I, 0.

Since the letters are repeating, the formula used would be

Where n is the remaining number of letters, p1 and p2 are the number of times the repeated terms occur.

The number of words in the list before the word starting with E

= words starting with letter A = 907200

5. How many 6-digit numbers can be formed from the digits 0, 1, 3, 5, 7 and 9, which are divisible by 10 and no digit is repeated?

Solution:

The number is divisible by 10 if the unit place has 0 in it.

The 6-digit number is to be formed out of which unit place is fixed as 0.

The remaining 5 places can be filled by 1, 3, 5, 7 and 9.

Here, n = 5

And the numbers of choice available are 5.

So, the total ways in which the rest of the places can be filled are 5P5

6. The English alphabet has 5 vowels and 21 consonants. How many words with two different vowels and 2 different consonants can be formed from the alphabet?

Solution:

We know that there are 5 vowels and 21 consonants in the English alphabet.

Choosing two vowels out of 5 would be done in 5C2 ways.

Choosing 2 consonants out of 21 can be done in 21C2 ways.

The total number of ways to select 2 vowels and 2 consonants

= 5C2 × 21C2

Each of these four letters can be arranged in four ways 4P4

The total numbers of words that can be formed are

24 × 2100 = 50400

7. In an examination, a question paper consists of 12 questions divided into two parts, i.e., Part I and Part II, containing 5 and 7 questions, respectively. A student is required to attempt 8 questions in all, selecting at least 3 from each part. In how many ways can a student select the questions?

Solution:

The student can choose 3 questions from part I and 5 from part II,

Or

4 questions from part I and 4 from part II,

5 questions from parts 1 and 3 from part II.

8. Determine the number of 5-card combinations out of a deck of 52 cards if each selection of 5 cards has exactly one king.

Solution:

We have a deck of cards that has 4 kings.

The numbers of remaining cards are 52.

Ways of selecting a king from the deck = 4C1

Ways of selecting the remaining 4 cards from 48 cards= 48C4

The total number of selecting the 5 cards having one king always

= 4C1 × 48C4

9. It is required to seat 5 men and 4 women in a row so that the women occupy even places. How many such arrangements are possible?

Solution:

Given, there is a total of 9 people.

Women occupy even places, which means they will be sitting in 2nd, 4th, 6th and 8th places, whereas men will be sitting in 1st, 3rd, 5th,7th and 9th places.

4 women can sit in four places and ways they can be seated= 4P4

5 men can occupy 5 seats in 5 ways.

The number of ways in which these can be seated = 5P5

The total number of sitting arrangements possible =

24 × 120 = 2880

10. From a class of 25 students, 10 are to be chosen for an excursion party. There are 3 students who decide that either all of them will join or none of them will join. In how many ways can the excursion party be chosen?

Solution:

In this question, we get 2 options that are

(i) Either all 3 will go

The remaining students in the class are: 25 – 3 = 22

The number of students that remain to be chosen for the party = 7

The number of ways to choose the remaining 22 students = 22C7

=

(ii) None of them will go.

The students going will be 10.

Remaining students eligible for going = 22

The number of ways in which these 10 students can be selected is 22C10

The total number of ways in which students can be chosen = 170544 + 646646 = 817190

11. In how many ways can the letters of the word ASSASSINATION be arranged so that all the S are together?

Solution:

In the given word ASSASSINATION, there are 4 ‘S’. Since all the 4 ‘S’ have to be arranged together, let us take them as one unit.

The remaining letters are= 3 ‘A’, 2 ‘I’, 2 ‘N’, T

The number of letters to be arranged is 9 (including 4 ‘S’)

Using the formula

where n is the number of terms and p1, p2 p3 are the number of times the repeating letters repeat themselves.

Here, p1= 3, p2= 2, p3 = 2

Putting the values in the formula, we get