NCERT Solutions for Class 11 Maths Chapter 7 – Binomial Theorem

The NCERT Solutions for Class 11 Maths Chapter 7 – Binomial Theorem of all the exercise are available here

NCERT textbook contains numerous questions which are intended for the students to solve and practise. To score high marks in the Class 11 examination, solving and practising the NCERT Solutions for Class 11 Maths is a must.

NCERT Solutions for Class 11 Maths Chapter 8 – Binomial Theorem Exercise 7.1 has questions on the following topics:

1. Introduction to Binomial Theorem
2. Binomial Theorem for Positive Integral Indices
3. Pascal’s Triangle
   • Binomial theorem for any positive integer n
   • Some special cases

NCERT Solutions Class 11 Maths Chapter 7 Binomial Theorem – Exercise 7.1

Expand each of the expressions in Exercises 1 to 5.

1. (1 – 2x)5

Solution:

From the binomial theorem expansion, we can write as

(1 – 2x)5

= 5Co (1)5 – 5C1 (1)4 (2x) + 5C2 (1)3 (2x)2 – 5C3 (1)2 (2x)3 + 5C4 (1)1 (2x)4 – 5C5 (2x)5

= 1 – 5 (2x) + 10 (4x)2 – 10 (8×3) + 5 ( 16 x4) – (32 x5)

= 1 – 10x + 40×2 – 80×3 + 80×4– 32×5

Solution:

From the binomial theorem, the given equation can be expanded as

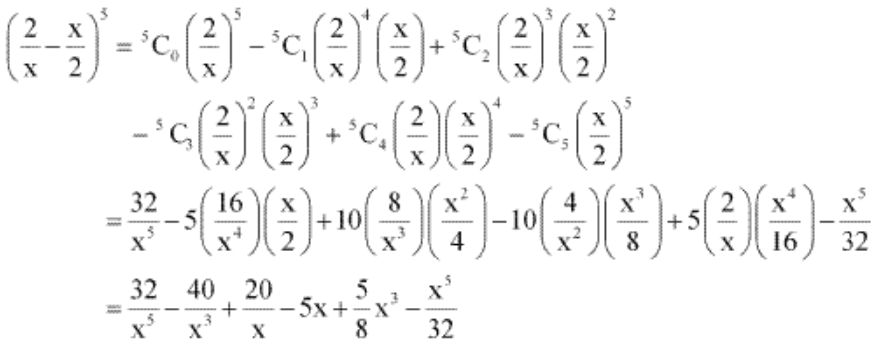
3. (2x – 3)6

Solution:

From the binomial theorem, the given equation can be expanded as

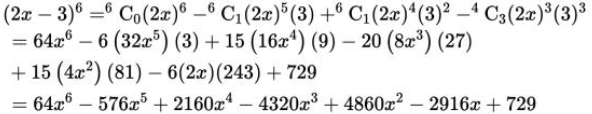
Solution:

From the binomial theorem, the given equation can be expanded as

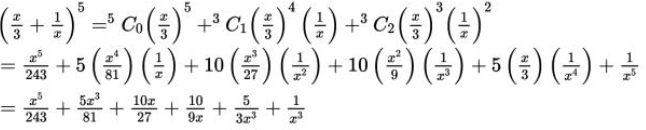
Solution:

From the binomial theorem, the given equation can be expanded as

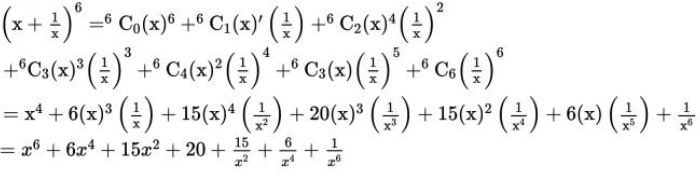
6. (96)3

Solution:

Given, (96)3

96 can be expressed as the sum or difference of two numbers, and then the binomial theorem can be applied.

The given question can be written as 96 = 100 – 4

(96)3 = (100 – 4)3

= 3C0 (100)3 – 3C1 (100)2 (4) – 3C2 (100) (4)2– 3C3 (4)3

= (100)3 – 3 (100)2 (4) + 3 (100) (4)2 – (4)3

= 1000000 – 120000 + 4800 – 64

= 884736

7. (102)5

Solution:

Given, (102)5

102 can be expressed as the sum or difference of two numbers, and then the binomial theorem can be applied.

The given question can be written as 102 = 100 + 2

(102)5 = (100 + 2)5

= 5C0 (100)5 + 5C1 (100)4 (2) + 5C2 (100)3 (2)2 + 5C3 (100)2 (2)3 + 5C4 (100) (2)4 + 5C5 (2)5

= (100)5 + 5 (100)4 (2) + 10 (100)3 (2)2 + 5 (100) (2)3 + 5 (100) (2)4 + (2)5

= 1000000000 + 1000000000 + 40000000 + 80000 + 8000 + 32

= 11040808032

8. (101)4

Solution:

Given, (101)4

101 can be expressed as the sum or difference of two numbers, and then the binomial theorem can be applied.

The given question can be written as 101 = 100 + 1

(101)4 = (100 + 1)4

= 4C0 (100)4 + 4C1 (100)3 (1) + 4C2 (100)2 (1)2 + 4C3 (100) (1)3 + 4C4 (1)4

= (100)4 + 4 (100)3 + 6 (100)2 + 4 (100) + (1)4

= 100000000 + 400000 + 60000 + 400 + 1

= 104060401

9. (99)5

Solution:

Given, (99)5

99 can be written as the sum or difference of two numbers, then the binomial theorem can be applied.

The given question can be written as 99 = 100 -1

(99)5 = (100 – 1)5

= 5C0 (100)5 – 5C1 (100)4 (1) + 5C2 (100)3 (1)2 – 5C3 (100)2 (1)3 + 5C4 (100) (1)4 – 5C5 (1)5

= (100)5 – 5 (100)4 + 10 (100)3 – 10 (100)2 + 5 (100) – 1

= 1000000000 – 5000000000 + 10000000 – 100000 + 500 – 1

= 9509900499

10. Using the Binomial Theorem, indicate which number is larger (1.1)10000 or 1000.

Solution:

By splitting the given 1.1 and then applying the binomial theorem, the first few terms of (1.1)10000 can be obtained as

(1.1)10000 = (1 + 0.1)10000

= (1 + 0.1)10000 C1 (1.1) + other positive terms

= 1 + 10000 × 1.1 + other positive terms

= 1 + 11000 + other positive terms

> 1000

(1.1)10000 > 1000

11. Find (a + b)4 – (a – b)4. Hence, evaluate

Solution:

Using the binomial theorem, the expression (a + b)4 and (a – b)4 can be expanded

(a + b)4 = 4C0 a4 + 4C1 a3 b + 4C2 a2 b2 + 4C3 a b3 + 4C4 b4

(a – b)4 = 4C0 a4 – 4C1 a3 b + 4C2 a2 b2 – 4C3 a b3 + 4C4 b4

Now, (a + b)4 – (a – b)4 = 4C0 a4 + 4C1 a3 b + 4C2 a2 b2 + 4C3 a b3 + 4C4 b4 – [4C0 a4 – 4C1 a3 b + 4C2 a2 b2 – 4C3 a b3 + 4C4 b4]

= 2 (4C1 a3 b + 4C3 a b3)

= 2 (4a3 b + 4ab3)

= 8ab (a2 + b2)

Now, by substituting a = √3 and b = √2, we get

(√3 + √2)4 – (√3 – √2)4 = 8 (√3) (√2) {(√3)2 + (√2)2}

= 8 (√6) (3 + 2)

= 40 √6

12. Find (x + 1)6 + (x – 1)6. Hence, or otherwise, evaluate

Solution:

Using the binomial theorem, the expressions (x + 1)6 and (x – 1)6 can be expressed as

(x + 1)6 = 6C0 x6 + 6C1 x5 + 6C2 x4 + 6C3 x3 + 6C4 x2 + 6C5 x + 6C6

(x – 1)6 = 6C0 x6 – 6C1 x5 + 6C2 x4 – 6C3 x3 + 6C4 x2 – 6C5 x + 6C6

Now, (x + 1)6 – (x – 1)6 = 6C0 x6 + 6C1 x5 + 6C2 x4 + 6C3 x3 + 6C4 x2 + 6C5 x + 6C6 – [6C0 x6 – 6C1 x5 + 6C2 x4 – 6C3 x3 + 6C4 x2 – 6C5 x + 6C6]

= 2 [6C0 x6 + 6C2 x4 + 6C4 x2 + 6C6]

= 2 [x6 + 15×4 + 15×2 + 1]

Now, by substituting x = √2, we get

(√2 + 1)6 – (√2 – 1)6 = 2 [(√2)6 + 15(√2)4 + 15(√2)2 + 1]

= 2 (8 + 15 × 4 + 15 × 2 + 1)

= 2 (8 + 60 + 30 + 1)

= 2 (99)

= 198

13. Show that 9n+1 – 8n – 9 is divisible by 64 whenever n is a positive integer.

Solution:

In order to show that 9n+1 – 8n – 9 is divisible by 64, it has to be shown that 9n+1 – 8n – 9 = 64 k, where k is some natural number

Using the binomial theorem,

(1 + a)m = mC0 + mC1 a + mC2 a2 + …. + m C m am

For a = 8 and m = n + 1, we get

(1 + 8)n+1 = n+1C0 + n+1C1 (8) + n+1C2 (8)2 + …. + n+1 C n+1 (8)n+1

9n+1 = 1 + (n + 1) 8 + 82 [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n-1]

9n+1 = 9 + 8n + 64 [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n-1]

9n+1 – 8n – 9 = 64 k

Where k = [n+1C2 + n+1C3 (8) + …. + n+1 C n+1 (8)n-1] is a natural number

Thus, 9n+1 – 8n – 9 is divisible by 64 whenever n is a positive integer.

Hence, the proof.

14. Prove that

Solution: