NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

NCERT Solutions Class 12 Maths Chapter 11 Three Dimensional Geometry are designed to help students learn different methodologies in which various questions from three dimensional geometry should be solved. Illustrating from daily life examples around us, we can observe that all the things in the real world are in a three-dimensional shape.

Three Dimensional Geometry is a concept which can easily be grasped. Therefore, SimplyAcad has provided these answers which covers all the exercises included in the textbook.

The solutions mentioned below are according to the latest update of the CBSE Syllabus for 2024-25. The solution will help in understanding the concepts of Three Dimensional Geometry thoroughly as the answers are explained in a stepwise manner. NCERT Solutions Class 12 Maths Chapter 11 Three Dimensional Geometry is an extremely important chapter which must be carefully taken from exam point of view.

NCERT Solutions Class 12 Maths Chapter 11 Three Dimensional Geometry Exercise 11.1

PAGE NO: 467

1. If a line makes angles 90°, 135°, 45° with the x, y and z-axes, respectively, find its direction cosines.

Solution:

Let the direction cosines of the line be l, m and n.

Here let α = 90°, β = 135° and γ = 45°

So,

l = cos α, m = cos β and n = cos γ

So, the direction cosines are

l = cos 90° = 0

m = cos 135°= cos (180° – 45°) = -cos 45° = -1/√2

n = cos 45° = 1/√2

∴ The direction cosines of the line are 0, -1/√2, 1/√2

2. Find the direction cosines of a line which makes equal angles with the coordinate axes.

Solution:

Given:

Angles are equal.

So, let the angles be α, β, γ

Let the direction cosines of the line be l, m and n.

l = cos α, m = cos β and n = cos γ

Here, given α = β = γ (Since, line makes equal angles with the coordinate axes) … (1)

The direction cosines are

l = cos α, m = cos β and n = cos γ

We have,

l2 + m 2 + n2 = 1

cos2 α + cos2β + cos2γ = 1

From (1) we have,

cos2 α + cos2 α + cos2 α = 1

3 cos2 α = 1

Cos α = ± √(1/3)

∴ The direction cosines are

l = ± √(1/3), m = ± √(1/3), n = ± √(1/3)

3. If a line has the direction ratios –18, 12, –4, then what are its direction cosines?

Solution:

Given:

Direction ratios as -18, 12, -4

Where, a = -18, b = 12, c = -4

Let us consider the direction ratios of the line as a, b and c

Then the direction cosines are

∴ The direction cosines are

-18/22, 12/22, -4/22 => -9/11, 6/11, -2/11

4. Show that the points (2, 3, 4), (–1, –2, 1), (5, 8, 7) are collinear.

Solution:

If the direction ratios of two lines segments are proportional, then the lines are collinear.

Given:

A(2, 3, 4), B(−1, −2, 1), C(5, 8, 7)

Direction ratio of line joining A (2, 3, 4) and B (−1, −2, 1), are

(−1−2), (−2−3), (1−4) = (−3, −5, −3)

Where, a1 = -3, b1 = -5, c1 = -3

Direction ratio of line joining B (−1, −2, 1) and C (5, 8, 7) are

(5− (−1)), (8− (−2)), (7−1) = (6, 10, 6)

Where, a2 = 6, b2 = 10 and c2 =6

Now,

∴ A, B, C are collinear.

5. Find the direction cosines of the sides of the triangle whose vertices are (3, 5, –4), (-1, 1, 2) and (–5, –5, –2).

Solution:

Given:

The vertices are (3, 5, –4), (-1, 1, 2) and (–5, –5, –2).

The direction cosines of the two points passing through A(x1, y1, z1) and B(x2, y2, z2) is given by (x2 – x1), (y2-y1), (z2-z1)

Firstly let us find the direction ratios of AB

Where, A = (3, 5, -4) and B = (-1, 1, 2)

Ratio of AB = [(x2 – x1)2, (y2 – y1)2, (z2 – z1)2]

= (-1-3), (1-5), (2-(-4)) = -4, -4, 6

Then by using the formula,

√[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

√[(-4)2 + (-4)2 + (6)2] = √(16+16+36)

= √68

= 2√17

Now let us find the direction cosines of the line AB

By using the formula,

-4/2√17 , -4/2√17, 6/2√17

Or -2/√17, -2/√17, 3/√17

Similarly,

Let us find the direction ratios of BC

Where, B = (-1, 1, 2) and C = (-5, -5, -2)

Ratio of AB = [(x2 – x1)2, (y2 – y1)2, (z2 – z1)2]

= (-5+1), (-5-1), (-2-2) = -4, -6, -4

Then by using the formula,

√[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

√[(-4)2 + (-6)2 + (-4)2] = √(16+36+16)

= √68

= 2√17

Now, let us find the direction cosines of the line AB

By using the formula,

-4/2√17, -6/2√17, -4/2√17

Or -2/√17, -3/√17, -2/√17

Similarly,

Let us find the direction ratios of CA

Where, C = (-5, -5, -2) and A = (3, 5, -4)

Ratio of AB = [(x2 – x1)2, (y2 – y1)2, (z2 – z1)2]

= (3+5), (5+5), (-4+2) = 8, 10, -2

Then, by using the formula,

√[(x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2]

√[(8)2 + (10)2 + (-2)2] = √(64+100+4)

= √168

= 2√42

Now, let us find the direction cosines of the line AB

By using the formula,

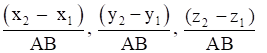
8/2√42, 10/2√42, -2/2√42

Or 4/√42, 5/√42, -1/√42

NCERT Solutions Class 12 Maths Chapter 11 Three Dimensional Geometry Exercise 11.2

PAGE NO: 477

1. Show that the three lines with direction cosines

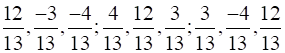Are mutually perpendicular.

Solution:

Let us consider the direction cosines of L1, L2 and L3 be l1, m1, n1; l2, m2, n2 and l3, m3, n3.

We know that

If l1, m1, n1 and l2, m2, n2 are the direction cosines of two lines,

And θ is the acute angle between the two lines,

Then cos θ = |l1l2 + m1m2 + n1n2|

If two lines are perpendicular, then the angle between the two is θ = 90°

For perpendicular lines, | l1l2 + m1m2 + n1n2 | = cos 90° = 0, i.e. | l1l2 + m1m2 + n1n2 | = 0

So, in order to check if the three lines are mutually perpendicular, we compute | l1l2 + m1m2 + n1n2 | for all the pairs of the three lines.

Firstly let us compute, | l1l2 + m1m2 + n1n2 |

So, L1⊥ L2 …… (1)

Similarly,

Let us compute, | l2l3 + m2m3 + n2n3 |

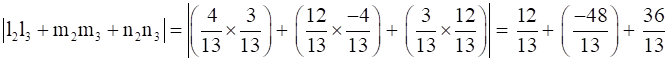
So, L2⊥ L3 ….. (2)

Similarly,

Let us compute, | l3l1 + m3m1 + n3n1 |

So, L1⊥ L3 ….. (3)

∴ By (1), (2) and (3), the lines are perpendicular.

L1, L2 and L3 are mutually perpendicular.

2. Show that the line through the points (1, –1, 2), (3, 4, –2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).

Solution:

Given:

The points (1, –1, 2), (3, 4, –2) and (0, 3, 2), (3, 5, 6).

Let us consider AB be the line joining the points, (1, -1, 2) and (3, 4, -2), and CD be the line through the points (0, 3, 2) and (3, 5, 6).

Now,

The direction ratios, a1, b1, c1 of AB are

(3 – 1), (4 – (-1)), (-2 – 2) = 2, 5, -4.

Similarly,

The direction ratios, a2, b2, c2 of CD are

(3 – 0), (5 – 3), (6 – 2) = 3, 2, 4.

Then, AB and CD will be perpendicular to each other, if a1a2 + b1b2 + c1c2 = 0

a1a2 + b1b2 + c1c2 = 2(3) + 5(2) + 4(-4)

= 6 + 10 – 16

= 0

∴ AB and CD are perpendicular to each other.

3. Show that the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (–1, –2, 1), (1, 2, 5).

Solution:

Given:

The points (4, 7, 8), (2, 3, 4) and (–1, –2, 1), (1, 2, 5).

Let us consider AB to be the line joining the points, (4, 7, 8), (2, 3, 4) and CD to be the line through the points (–1, –2, 1), (1, 2, 5).

Now,

The direction ratios, a1, b1, c1 of AB are

(2 – 4), (3 – 7), (4 – 8) = -2, -4, -4.

The direction ratios, a2, b2, c2 of CD are

(1 – (-1)), (2 – (-2)), (5 – 1) = 2, 4, 4.

Then, AB will be parallel to CD, if

So, a1/a2 = -2/2 = -1

b1/b2 = -4/4 = -1

c1/c2 = -4/4 = -1

∴ We can say that,

-1 = -1 = -1

Hence, AB is parallel to CD where the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (–1, –2, 1), (1, 2, 5)

4. Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector .

Solution:

5. Find the equation of the line in vector and in Cartesian form that passes through the point with position vector and is in the direction

Solution:

6. Find the Cartesian equation of the line which passes through the point (–2, 4, –5) and parallel to the line given by

Solution:

Given:

The points (-2, 4, -5)

We know that the Cartesian equation of a line through a point (x1, y1, z1) and having direction ratios a, b, c is

7. The Cartesian equation of a line is

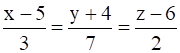. Write its vector form.

Solution:

So when comparing this standard form with the given equation, we get

x1 = 5, y1 = -4, z1 = 6 and

l = 3, m = 7, n = 2

8. Find the vector and the Cartesian equations of the lines that passes through the origin and (5, –2, 3).

Solution:

9. Find the vector and the Cartesian equations of the line that passes through the points (3, –2, –5), (3, –2, 6).

Solution:

10. Find the angle between the following pairs of lines:

Solution:

So,

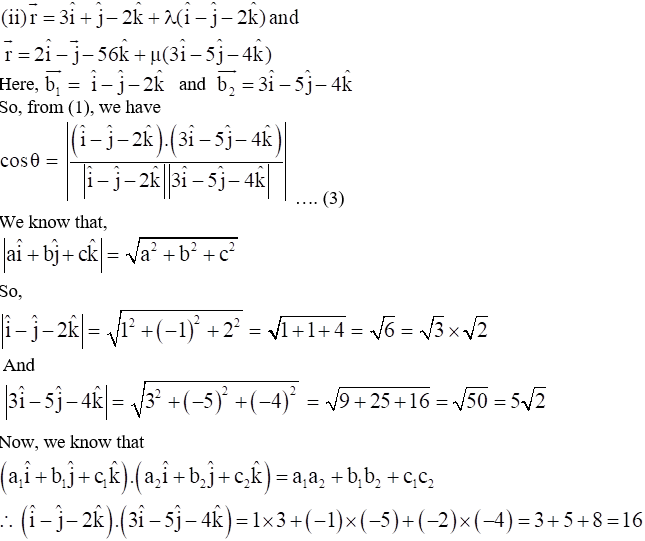
By (3), we have

11. Find the angle between the following pair of lines:

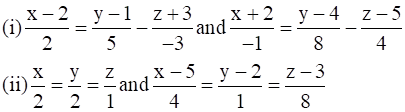
Solution:

12. Find the values of p so that the lines

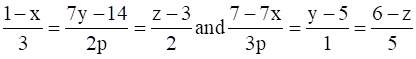are at right angles.

Solution:

So, the direction ratios of the lines are

-3, 2p/7, 2 and -3p/7, 1, -5

Now, as both the lines are at right angles,

So, a1a2 + b1b2 + c1c2 = 0

(-3) (-3p/7) + (2p/7) (1) + 2 (-5) = 0

9p/7 + 2p/7 – 10 = 0

(9p+2p)/7 = 10

11p/7 = 10

11p = 70

p = 70/11

∴ The value of p is 70/11

13. Show that the lines

are perpendicular to each other.

Solution:

The equations of the given lines are

Two lines with direction ratios is given as

a1a2 + b1b2 + c1c2 = 0

So the direction ratios of the given lines are 7, -5, 1 and 1, 2, 3

i.e., a1 = 7, b1 = -5, c1 = 1 and

a2 = 1, b2 = 2, c2 = 3

Now, considering

a1a2 + b1b2 + c1c2 = 7 × 1 + (-5) × 2 + 1 × 3

= 7 -10 + 3

= – 3 + 3

= 0

∴ The two lines are perpendicular to each other.

14. Find the shortest distance between the lines

Solution:

Let us rationalizing the fraction by multiplying the numerator and denominator by √2, we get

∴ The shortest distance is 3√2/2

15. Find the shortest distance between the lines

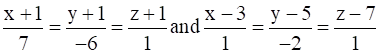
Solution:

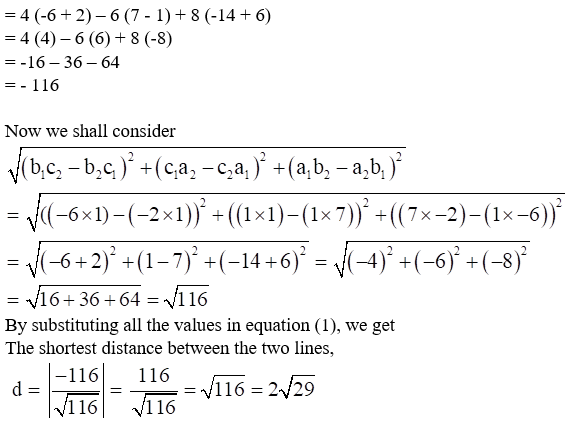
∴ The shortest distance is 2√29

16. Find the shortest distance between the lines whose vector equations are

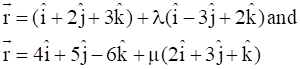
Solution:

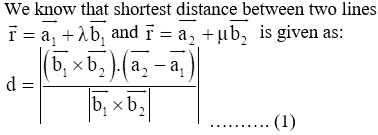
Here by comparing the equations we get,

∴ The shortest distance is 3√19

17. Find the shortest distance between the lines whose vector equations are

Solution:

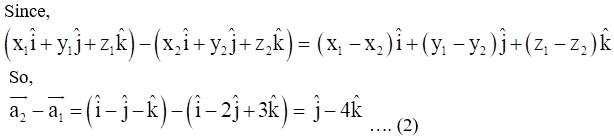
And,

∴ The shortest distance is 8√29

NCERT Solutions Class 12 Maths Chapter 11 Three Dimensional Geometry Exercise 11.3

PAGE NO: 493

1. In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
(a) z = 2

(b) x + y + z = 1

(c) 2x + 3y – z = 5

(d) 5y + 8 = 0

Solution:

(a) z = 2

Given:

The equation of the plane, z = 2 or 0x + 0y + z = 2 …. (1)

Direction ratio of the normal (0, 0, 1)

By using the formula,

√[(0)2 + (0)2 + (1)2] = √1

= 1

Now,

Divide both the sides of equation (1) by 1, we get

0x/(1) + 0y/(1) + z/1 = 2

So this is of the form lx + my + nz = d

Where, l, m, n are the direction cosines and d is the distance

∴ The direction cosines are 0, 0, 1

Distance (d) from the origin is 2 units

(b) x + y + z = 1

Given:

The equation of the plane, x + y + z = 1…. (1)

Direction ratio of the normal (1, 1, 1)

By using the formula,

√[(1)2 + (1)2 + (1)2] = √3

Now,

Divide both the sides of equation (1) by √3, we get

x/(√3) + y/(√3) + z/(√3) = 1/√3

So this is of the form lx + my + nz = d

Where, l, m, n are the direction cosines and d is the distance

∴ The direction cosines are 1/√3, 1/√3, 1/√3

Distance (d) from the origin is 1/√3 units

(c) 2x + 3y – z = 5

Given:

The equation of the plane, 2x + 3y – z = 5…. (1)

Direction ratio of the normal (2, 3, -1)

By using the formula,

√[(2)2 + (3)2 + (-1)2] = √14

Now,

Divide both the sides of equation (1) by √14, we get

2x/(√14) + 3y/(√14) – z/(√14) = 5/√14

So this is of the form lx + my + nz = d

Where, l, m, n are the direction cosines and d is the distance

∴ The direction cosines are 2/√14, 3/√14, -1/√14

Distance (d) from the origin is 5/√14 units

(d) 5y + 8 = 0

Given:

The equation of the plane, 5y + 8 = 0

-5y = 8 or

0x – 5y + 0z = 8…. (1)

Direction ratio of the normal (0, -5, 0)

By using the formula,

√[(0)2 + (-5)2 + (0)2] = √25

= 5

Now,

Divide both the sides of equation (1) by 5, we get

0x/(5) – 5y/(5) – 0z/(5) = 8/5

So this is of the form lx + my + nz = d

Where, l, m, n are the direction cosines and d is the distance

∴ The direction cosines are 0, -1, 0

Distance (d) from the origin is 8/5 units

2. Find the vector equation of a plane which is at a distance of 7 units from the origin and normal to the vector

Solution:

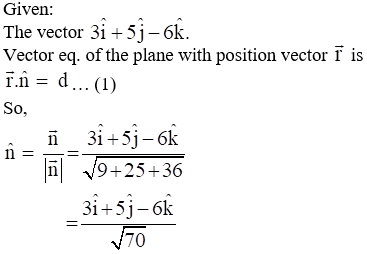
3. Find the Cartesian equation of the following planes:
(a)

Solution:

Given:

The equation of the plane.

4. In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
(a) 2x + 3y + 4z – 12 = 0

(b) 3y + 4z – 6 = 0

(c) x + y + z = 1

(d) 5y + 8 = 0

Solution:

(a) 2x + 3y + 4z – 12 = 0

Let the coordinate of the foot of ⊥ P from the origin to the given plane be P(x, y, z).

2x + 3y + 4z = 12 …. (1)

Direction ratio are (2, 3, 4)

√[(2)2 + (3)2 + (4)2] = √(4 + 9 + 16)

= √29

Now,

Divide both the sides of equation (1) by √29, we get

2x/(√29) + 3y/(√29) + 4z/(√29) = 12/√29

So this is of the form lx + my + nz = d

Where, l, m, n are the direction cosines and d is the distance

∴ The direction cosines are 2/√29, 3/√29, 4/√29

Coordinate of the foot (ld, md, nd) =

= [(2/√29) (12/√29), (3/√29) (12/√29), (4/√29) (12/√29)]

= 24/29, 36/29, 48/29

(b) 3y + 4z – 6 = 0

Let the coordinate of the foot of ⊥ P from the origin to the given plane be P(x, y, z).

0x + 3y + 4z = 6 …. (1)

Direction ratio are (0, 3, 4)

√[(0)2 + (3)2 + (4)2] = √(0 + 9 + 16)

= √25

= 5

Now,

Divide both the sides of equation (1) by 5, we get

0x/(5) + 3y/(5) + 4z/(5) = 6/5

So this is of the form lx + my + nz = d

Where, l, m, n are the direction cosines and d is the distance

∴ The direction cosines are 0/5, 3/5, 4/5

Coordinate of the foot (ld, md, nd) =

= [(0/5) (6/5), (3/5) (6/5), (4/5) (6/5)]

= 0, 18/25, 24/25

(c) x + y + z = 1

Let the coordinate of the foot of ⊥ P from the origin to the given plane be P(x, y, z).

x + y + z = 1 …. (1)

Direction ratio are (1, 1, 1)

√[(1)2 + (1)2 + (1)2] = √(1 + 1 + 1)

= √3

Now,

Divide both the sides of equation (1) by √3, we get

1x/(√3) + 1y/(√3) + 1z/(√3) = 1/√3

So this is of the form lx + my + nz = d

Where, l, m, n are the direction cosines and d is the distance

∴ The direction cosines are 1/√3, 1/√3, 1/√3

Coordinate of the foot (ld, md, nd) =

= [(1/√3) (1/√3), (1/√3) (1/√3), (1/√3) (1/√3)]

= 1/3, 1/3, 1/3

(d) 5y + 8 = 0

Let the coordinate of the foot of ⊥ P from the origin to the given plane be P(x, y, z).

0x – 5y + 0z = 8 …. (1)

Direction ratio are (0, -5, 0)

√[(0)2 + (-5)2 + (0)2] = √(0 + 25 + 0)

= √25

= 5

Now,

Divide both the sides of equation (1) by 5, we get

0x/(5) – 5y/(5) + 0z/(5) = 8/5

So this is of the form lx + my + nz = d

Where, l, m, n are the direction cosines and d is the distance

∴ The direction cosines are 0, -1, 0

Coordinate of the foot (ld, md, nd) =

= [(0/5) (8/5), (-5/5) (8/5), (0/5) (8/5)]

= 0, -8/5, 0

5. Find the vector and Cartesian equations of the planes

(a) that passes through the point (1, 0, –2) and the normal to the plane is

(b) that passes through the point (1,4, 6) and the normal vector to the plane is

Solution:

x – 1 – 2y + 8 + z – 6 = 0

x – 2y + z + 1 = 0

x – 2y + z = -1

∴ The required Cartesian equation of the plane is x – 2y + z = -1

x – 1 – 2y + 8 + z – 6 = 0

x – 2y + z + 1 = 0

x – 2y + z = -1

∴ The required Cartesian equation of the plane is x – 2y + z = -1

6. Find the equations of the planes that passes through three points.
(a) (1, 1, –1), (6, 4, –5), (–4, –2, 3)

(b) (1, 1, 0), (1, 2, 1), (–2, 2, –1)

Solution:

Given:

The points are (1, 1, -1), (6, 4, -5), (-4, -2, 3).

Let,

= 1(12 – 10) – 1(18 – 20) -1 (-12 + 16)

= 2 + 2 – 4

= 0

Since, the value of determinant is 0.

∴ The points are collinear as there will be infinite planes passing through the 3 given points.

(b) (1, 1, 0), (1, 2, 1), (–2, 2, –1)

7. Find the intercepts cut off by the plane 2x + y – z = 5.

Solution:

Given:

The plane 2x + y – z = 5

Let us express the equation of the plane in intercept form

x/a + y/b + z/c = 1

Where a, b, c are the intercepts cut-off by the plane at x, y and z axes, respectively.

2x + y – z = 5 …. (1)

Now dividing both the sides of equation (1) by 5, we get

2x/5 + y/5 – z/5 = 5/5

2x/5 + y/5 – z/5 = 1

x/(5/2) + y/5 + z/(-5) = 1

Here, a = 5/2, b = 5 and c = -5

∴ The intercepts cut-off by the plane are 5/2, 5 and -5.

8. Find the equation of the plane with intercept 3 on the y-axis and parallel to ZOX plane.

Solution:

We know that the equation of the plane ZOX is y = 0

So, the equation of plane parallel to ZOX is of the form, y = a

Since the y-intercept of the plane is 3, a = 3

∴ The required equation of the plane is y = 3

9. Find the equation of the plane through the intersection of the planes 3x – y + 2z – 4 = 0 and x + y + z – 2 = 0 and the point (2, 2, 1).

Solution:

Given:

Equation of the plane passes through the intersection of the plane is given by

(3x – y + 2z – 4) + λ (x + y + z – 2) = 0 and the plane passes through the points (2, 2, 1).

So, (3 × 2 – 2 + 2 × 1 – 4) + λ (2 + 2 + 1 – 2) = 0

2 + 3λ = 0

3λ = -2

λ = -2/3 …. (1)

Upon simplification, the required equation of the plane is given as

(3x – y + 2z – 4) – 2/3 (x + y + z – 2) = 0

(9x – 3y + 6z – 12 – 2x – 2y – 2z + 4)/3 = 0

7x – 5y + 4z – 8 = 0

∴ The required equation of the plane is 7x – 5y + 4z – 8 = 0

10. Find the vector equation of the plane passing through the intersection of the planes and through the point (2, 1, 3).

Solution:

The equation of any plane through the intersection of the planes given in equations (1) and (2) is given by,

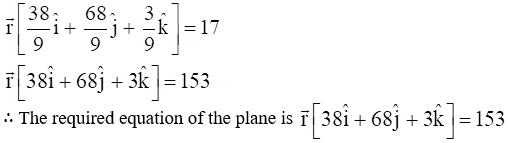
11. Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.

Solution:

Let the equation of the plane that passes through the two-given planes

x + y + z = 1 and 2x + 3y + 4z = 5 is

(x + y + z – 1) + λ (2x + 3y + 4z – 5) = 0

(2λ + 1) x + (3λ + 1) y + (4λ + 1) z -1 – 5λ = 0…… (1)

So the direction ratio of the plane is (2λ + 1, 3λ + 1, 4λ + 1)

And direction ratio of another plane is (1, -1, 1)

Since, both the planes are ⊥

So by substituting in a1a2 + b1b2 + c1c2 = 0

(2λ + 1 × 1) + (3λ + 1 × (-1)) + (4λ + 1 × 1) = 0

2λ + 1 – 3λ – 1 + 4λ + 1 = 0

3λ + 1 = 0

λ = -1/3

Substitute the value of λ in equation (1) we get,

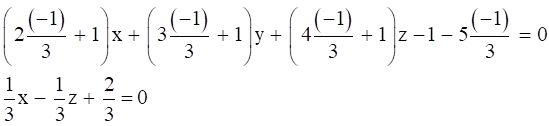
x – z + 2 = 0

∴ The required equation of the plane is x – z + 2 = 0

12. Find the angle between the planes whose vector equations are

Solution:

13. In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
(a) 7x + 5y + 6z + 30 = 0 and 3x – y – 10z + 4 = 0

(b) 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0

(c) 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0

(d) 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0

(e) 4x + 8y + z – 8 = 0 and y + z – 4 = 0

Solution:

(a) 7x + 5y + 6z + 30 = 0 and 3x – y – 10z + 4 = 0

Given:

The equation of the given planes are

7x + 5y + 6z + 30 = 0 and 3x – y – 10z + 4 = 0

Two planes are ⊥ if the direction ratio of the normal to the plane is

a1a2 + b1b2 + c1c2 = 0

21 – 5 – 60

-44 ≠ 0

Both the planes are not ⊥ to each other.

Now, two planes are || to each other if the direction ratio of the normal to the plane is

∴ The angle is cos-1 (2/5)

(b) 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0

Given:

The equation of the given planes are

2x + y + 3z – 2 = 0 and x – 2y + 5 = 0

Two planes are ⊥ if the direction ratio of the normal to the plane is

a1a2 + b1b2 + c1c2 = 0

2 × 1 + 1 × (-2) + 3 × 0

= 0

∴ The given planes are ⊥ to each other.

(c) 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0

Given:

The equation of the given planes are

2x – 2y + 4z + 5 =0 and x – 2y + 5 = 0

We know that, two planes are ⊥ if the direction ratio of the normal to the plane is

a1a2 + b1b2 + c1c2 = 0

6 + 6 + 24

36 ≠ 0

∴ Both the planes are not ⊥ to each other.

Now let us check, both planes are || to each other if the direction ratio of the normal to the plane is

∴ The given planes are || to each other.

(d) 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0

Given:

The equation of the given planes are

2x – y + 3z – 1 = 0 and 2x – y + 3z + 3 = 0

We know that, two planes are ⊥ if the direction ratio of the normal to the plane is

a1a2 + b1b2 + c1c2 = 0

2 × 2 + (-1) × (-1) + 3 × 3

14 ≠ 0

∴ Both the planes are not ⊥ to each other.

Now, let us check two planes are || to each other if the direction ratio of the normal to the plane is

∴ The given planes are || to each other.

(e) 4x + 8y + z – 8 = 0 and y + z – 4 = 0

Given:

The equation of the given planes are

4x + 8y + z – 8 = 0 and y + z – 4 = 0

We know that, two planes are ⊥ if the direction ratio of the normal to the plane is

a1a2 + b1b2 + c1c2 = 0

0 + 8 + 1

9 ≠ 0

∴ Both the planes are not ⊥ to each other.

Now let us check, two planes are || to each other if the direction ratio of the normal to the plane is

∴ Both the planes are not || to each other.

Now let us find the angle between them, which is given as

∴ The angle is 45o.

14. In the following cases, find the distance of each of the given points from the corresponding given plane.
Point Plane
(a) (0, 0, 0) 3x – 4y + 12 z = 3

(b) (3, -2, 1) 2x – y + 2z + 3 = 0

(c) (2, 3, -5) x + 2y – 2z = 9

(d) (-6, 0, 0) 2x – 3y + 6z – 2 = 0

Solution:

(a) Point Plane

(0, 0, 0) 3x – 4y + 12 z = 3

We know that, distance of point P(x1, y1, z1) from the plane Ax + By + Cz – D = 0 is given as:

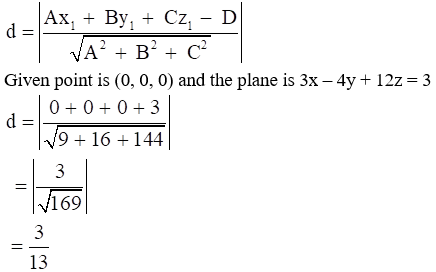
Given point is (0, 0, 0) and the plane is 3x – 4y + 12z = 3

= |3/√169|

= 3/13

∴ The distance is 3/13.

(b) Point Plane

(3, -2, 1) 2x – y + 2z + 3 = 0

We know that, distance of point P(x1, y1, z1) from the plane Ax + By + Cz – D = 0 is given as:

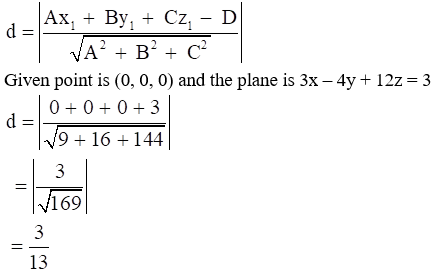
Given point is (3, -2, 1) and the plane is 2x – y + 2z + 3 = 0

= |13/√9|

= 13/3

∴ The distance is 13/3.

(c) Point Plane

(2, 3, -5) x + 2y – 2z = 9

We know that, distance of point P(x1, y1, z1) from the plane Ax + By + Cz – D = 0 is given as:

Given point is (2, 3, -5) and the plane is x + 2y – 2z = 9

= |9/√9|

= 9/3

= 3

∴ The distance is 3.

(d) Point Plane

(-6, 0, 0) 2x – 3y + 6z – 2 = 0

We know that, distance of point P(x1, y1, z1) from the plane Ax + By + Cz – D = 0 is given as:

Given point is (-6, 0, 0) and the plane is 2x – 3y + 6z – 2 = 0

= |14/√49|

= 14/7

= 2

∴ The distance is 2.

NCERT Solutions Class 12 Maths Chapter 11 Three Dimensional Geometry Miscellaneous Exercise

PAGE NO: 497

1. Show that the line joining the origin to the point (2, 1, 1) is perpendicular to the line determined by the points (3, 5, –1), (4, 3, –1).

Solution:

Let us consider OA to be the line joining the origin (0, 0, 0) and the point A (2, 1, 1).

And let BC be the line joining the points B (3, 5, −1) and C (4, 3, −1)

So the direction ratios of OA = (a1, b1, c1) ≡ [(2 – 0), (1 – 0), (1 – 0)] ≡ (2, 1, 1)

And the direction ratios of BC = (a2, b2, c2) ≡ [(4 – 3), (3 – 5), (-1 + 1)] ≡ (1, -2, 0)

Given:

OA is ⊥ to BC

Now we have to prove that:

a1a2 + b1b2 + c1c2 = 0

Let us consider LHS: a1a2 + b1b2 + c1c2

a1a2 + b1b2 + c1c2 = 2 × 1 + 1 × (−2) + 1 × 0

= 2 – 2

= 0

We know that R.H.S is 0

So LHS = RHS

∴ OA is ⊥ to BC

Hence proved.

2. If l1, m1, n1 and l2, m2, n2 are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are (m1n2 – m2n1), (n1l2 – n2l1), (l1m2 – l2m1)

Solution:

Let us consider l, m, n to be the direction cosines of the line perpendicular to each of the given lines.

Then, ll1 + mm1 + nn1 = 0 … (1)

And ll2 + mm2 + nn2 = 0 … (2)

Upon solving (1) and (2) by using cross – multiplication, we get

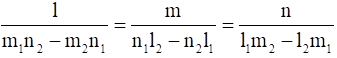
Thus, the direction cosines of the given line are proportional to

(m1n2 – m2n1), (n1l2 – n2l1), (l1m2 – l2m1)

So, its direction cosines are

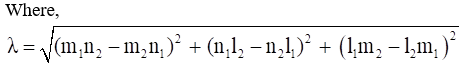
We know that

(l12 + m12 + n12) (l22 + m22 + n22) – (l1l2 + m1m2 + n1n2)2

= (m1n2 – m2n1)2 + (n1l2 – n2l1)2 + (l1m2 – l2m1)2 … (3)

It is given that the given lines are perpendicular to each other.

So, l1l2 + m1m2 + n1n2 = 0

Also, we have

l12 + m12 + n12 = 1

And, l22 + m22 + n22 = 1

Substituting these values in equation (3), we get

(m1n2 – m2n1)2 + (n1l2 – n2l1)2 + (l1m2 – l2m1)2 = 1

λ = 1

Hence, the direction cosines of the given line are (m1n2 – m2n1), (n1l2 – n2l1), (l1m2 – l2m1)

3. Find the angle between the lines whose direction ratios are a, b, c and b – c, c – a, a – b.

Solution:

Angle between the lines with direction ratios a1, b1, c1 and a2, b2, c2 is given by

Given:

a1 = a, b1 = b, c1 = c

a2 = b – c, b2 = c – a, c2 = a – b

Let us substitute the values in the above equation. We get,

= 0

Cos θ = 0

So, θ = 90° [Since, cos 90 = 0]

Hence, Angle between the given pair of lines is 90°.

4. Find the equation of a line parallel to x – axis and passing through the origin.

Solution:

We know that, equation of a line passing through (x1, y1, z1) and parallel to a line with direction ratios a, b, c is

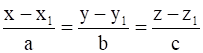
Given: the line passes through origin i.e. (0, 0, 0)

x1 = 0, y1 = 0, z1 = 0

Since line is parallel to x – axis,

a = 1, b = 0, c = 0

∴ Equation of Line is given by

5. If the coordinates of the points A, B, C, D be (1, 2, 3), (4, 5, 7), (–4, 3, –6) and (2, 9, 2), respectively, then find the angle between the lines AB and CD.

Solution:

We know that the angle between the lines with direction ratios a1, b1, c1 and a2, b2, c2 is given by

So now, a line passing through A (x1, y1, z1) and B (x2, y2, z2) has direction ratios (x1 – x2), (y1 – y2), (z1 – z2)

The direction ratios of line joining the points A (1, 2, 3) and B (4, 5, 7)

= (4 – 1), (5 – 2), (7 – 3)

= (3, 3, 4)

∴ a1 = 3, b1 = 3, c1 = 4

The direction ratios of line joining the points C (-4, 3, -6) and B (2, 9, 2)

= (2 – (-4)), (9 – 3), (2-(-6))

= (6, 6, 8)

∴ a2 = 6, b2 = 6, c2 = 8

Now let us substitute the values in the above equation. We get,

6. If the lines

and
are perpendicular, find the value of k.

Solution:

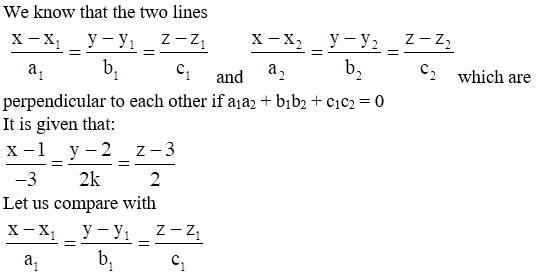
We get –

x2 = 1, y2 = 2, z2 = 3

And a2 = 3k, b2 = 1, c2 = -5

Since the two lines are perpendicular,

a1a2 + b1b2 + c1c2 = 0

(-3) × 3k + 2k × 1 + 2 × (-5) = 0

-9k + 2k – 10 = 0

-7k = 10

k = -10/7

∴ The value of k is -10/7.

7. Find the vector equation of the line passing through (1, 2, 3) and perpendicular to the plane

Solution:

8. Find the equation of the plane passing through (a, b, c) and parallel to the plane

Solution:

The equation of a plane passing through (x1, y1, z1) and perpendicular to a line with direction ratios A, B, C is given as

A (x – x1) + B (y – y1) + C (z – z1) = 0

It is given that, the plane passes through (a, b, c)

So, x1 = a, y1 = b, z1 = c

Since both planes are parallel to each other, their normal will be parallel

Direction ratios of normal = (1, 1, 1)

So, A = 1, B =1, C = 1

The Equation of plane in Cartesian form is given as

A (x – x1) + B (y – y1) + C (z – z1) = 0

1(x – a) + 1(y – b) + 1(z – c) = 0

x + y + z – (a + b + c) = 0

x + y + z = a + b + c

∴ The required equation of plane is x + y + z = a + b + c

9. Find the shortest distance between lines
and

Solution:

10. Find the coordinates of the point where the line through (5, 1, 6) and (3, 4,1) crosses the YZ – plane.

Solution:

We know that, two vectors are equal if their corresponding components are equal

So,

0 = 5 – 2λ

5 = 2λ

λ = 5/2

y = 1 + 3λ … (5)

And,

z = 6 – 5λ … (6)

Substituting the value of λ in equation (5) and (6), we get –

y = 1 + 3λ

= 1 + 3 × (5/2)

= 1 + (15/2)

= 17/2

And

z = 6 – 5λ

= 6 – 5 × (5/2)

= 6 – (25/2)

= – 13/2

∴ The coordinates of the required point is (0, 17/2, -13/2).

11. Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the ZX – plane.

Solution:

We know that, two vectors are equal if their corresponding components are equal

So,

x = 5 – 2λ … (5)

0 = 1 + 3λ

-1 = 3λ

λ = -1/3

And,

z = 6 – 5λ … (6)

Substituting the value of λ in equation (5) and (6), we get –

x = 5 – 2λ

= 5 – 2 × (-1/3)

= 5 + (2/3)

= 17/3

And

z = 6 – 5λ

= 6 – 5 × (-1/3)

= 6 + (5/3)

= 23/3

∴ The coordinates of the required point is (17/3, 0, 23/3).

12. Find the coordinates of the point where the line through (3, –4, –5) and (2, –3, 1) crosses the plane 2x + y + z = 7.

Solution:

We know that the equation of a line passing through two points A (x1, y1, z1) and B (x2, y2, z2) is given as

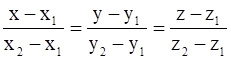
It is given that the line passes through the points A (3, –4, –5) and B (2, –3, 1)

So, x1 = 3, y1 = -4, z1 = -5

And, x2 = 2, y2 = -3, z2 = 1

Then the equation of line is

So, x = -k + 3 |, y = k – 4 |, z = 6k – 5 … (1)

Now let (x, y, z) be the coordinates of the point where the line crosses the given plane 2x + y + z + 7 = 0

By substituting the value of x, y, z in equation (1) in the equation of plane, we get

2x + y + z + 7 = 0

2(-k + 3) + (k – 4) + (6k – 5) = 7

5k – 3 = 7

5k = 10

k = 2

Now substituting the value of k in x, y, z we get,

x = – k + 3 = – 2 + 3 = 1

y = k – 4 = 2 – 4 = – 2

z = 6k – 5 = 12 – 5 = 7

∴ The coordinates of the required point are (1, -2, 7).

13. Find the equation of the plane passing through the point (–1, 3, 2) and perpendicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.

Solution:

We know that the equation of a plane passing through (x1, y1, z1) is given by

A (x – x1) + B (y – y1) + C (z – z1) = 0

Where, A, B, C are the direction ratios of normal to the plane.

It is given that the plane passes through (-1, 3, 2)

So, equation of plane is given by

A (x + 1) + B (y – 3) + C (z – 2) = 0 ……… (1)

Since this plane is perpendicular to the given two planes. So, their normal to the plane would be perpendicular to normal of both planes.

We know that

So, the required normal is the cross product of normal of planes

x + 2y + 3z = 5 and 3x + 3y + z = 0

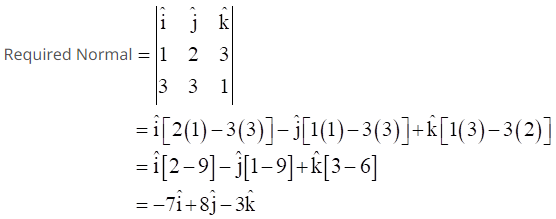
Hence, the direction ratios are = -7, 8, -3

∴ A = -7, B = 8, C = -3

Substituting the obtained values in equation (1), we get

A (x + 1) + B (y – 3) + C (z – 2) = 0

-7(x + 1) + 8(y – 3) + (-3) (z – 2) = 0

-7x – 7 + 8y – 24 – 3z + 6 = 0

-7x + 8y – 3z – 25 = 0

7x – 8y + 3z + 25 = 0

∴ The equation of the required plane is 7x – 8y + 3z + 25 = 0.

14. If the points (1, 1, p) and (–3, 0, 1) be equidistant from the plane

, then find the value of p.

Solution:

20 – 12p = ± 8

20 – 12p = 8 or, 20 – 12p = -8

12p = 12 or, 12p = 28

p = 1 or, p = 7/3

∴ The possible values of p are 1 and 7/3.

15. Find the equation of the plane passing through the line of intersection of the planes and and parallel to x-axis.

Solution:

Since this plane is parallel to the x-axis.

So, the normal vector of the plane (1) will be perpendicular to the x-axis.

The direction ratios of Normal (a1, b1, c1) ≡ [(1 – 2λ), (1 – 3λ), (1 +)]

The direction ratios of the x–axis (a2, b2, c2) ≡ (1, 0, 0)

Since the two lines are perpendicular,

a1a2 + b1b2 + c1c2 = 0

(1 – 2λ) × 1 + (1 – 3λ) × 0 + (1 + λ) × 0 = 0

(1 – 2λ) = 0

λ = 1/2

Substituting the value of λ in equation (1), we get

16. If O be the origin and the coordinates of P be (1, 2, –3), then find the equation of the plane passing through P and perpendicular to OP.

Solution:

We know that the equation of a plane passing through (x1, y1, z1) and perpendicular to a line with direction ratios A, B, C is given as

A(x – x1) + B(y – y1) + C (z – z1) = 0

It is given that the plane passes through P (1, 2, 3)

So, x1 = 1, y1 = 2, z1 = – 3

Normal vector to plane is =

Where O (0, 0, 0), P (1, 2, -3)

So, direction ratios of

is = (1 – 0), (2 – 0), (-3 – 0)

= (1, 2, – 3)

Where, A = 1, B = 2, C = -3

Equation of plane in Cartesian form is given as

1(x – 1) + 2(y – 2) – 3(z – (-3)) = 0

x – 1 + 2y – 4 – 3z – 9 = 0

x + 2y – 3z – 14 = 0

∴ The equation of the required plane is x + 2y – 3z – 14 = 0

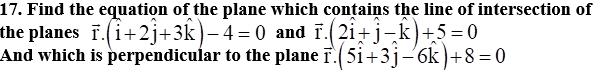
Solution:

Since this plane is perpendicular to the plane

So, the normal vector of the plane (1) will be perpendicular to the normal vector of plane (2).

Direction ratios of the normal of plane (1) = (a1, b1, c1) ≡ [(1 – 2λ), (2 – λ), (3 + λ)]

Direction ratios of the normal of plane (2) = (a2, b2, c2) ≡ (-5, -3, 6)

Since the two lines are perpendicular,

a1a2 + b1b2 + c1c2 = 0

(1 – 2λ) × (-5) + (2 – λ) × (-3) + (3 + λ) × 6 = 0

-5 + 10λ – 6 + 3λ + 18 + 6λ = 0

19λ + 7 = 0

λ = -7/19

By substituting the value of λ in equation (1), we get

18. Find the distance of the point (–1, –5, –10) from the point of intersection of the line

Solution:

Where,

x = 2, y = -1, z = 2

So, the point of intersection is (2, -1, 2).

Now, the distance between points (x1, y1, z1) and (x2, y2, z2) is given by

∴ The distance is 13 units.

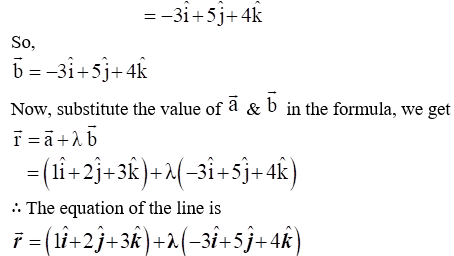
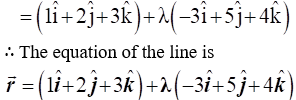
20. Find the vector equation of the line passing through the point (1, 2, – 4) and perpendicular to the two lines:
and .

Solution:

21. Prove that if a plane has the intercepts a, b, c and is at a distance of p units from the origin, then

Solution:

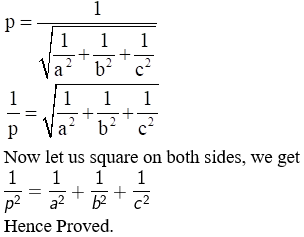
22. Distance between the two planes: 2x + 3y + 4z = 4 and 4x + 6y + 8z = 12 is
A. 2 units
B. 4 units
C. 8 units

D. 2/√29 units

Solution:

We know that the distance between two parallel planes Ax + By + Cz = d1 and Ax + By + Cz = d2 is given as

It is given that:

First Plane:

2x + 3y + 4z = 4

Let us compare with Ax + By + Cz = d1, we get

A = 2, B = 3, C = 4, d1 = 4

Second Plane:

4x + 6y + 8z = 12 [Divide the equation by 2]

We get,

2x + 3y + 4z = 6

Now comparing with Ax + By + Cz = d1, we get

A = 2, B = 3, C = 4, d2 = 6

So,

Distance between two planes is given as

= 2/√29

∴ Option (D) is the correct option.

23. The planes: 2x – y + 4z = 5 and 5x – 2.5y + 10z = 6 are
A. Perpendicular
B. Parallel
C. intersect y–axis
D. passes through

Solution:

It is given that:

First Plane:

2x – y + 4z = 5 [Multiply both sides by 2.5]

We get,

5x – 2.5y + 10z = 12.5 … (1)

Given second Plane:

5x – 2.5y + 10z = 6 … (2)

So,

It is clear that the direction ratios of normal of both the plane (1) and (2) are the same.

∴ Both the given planes are parallel.