</tr></td>Application of Integralslt;strong>Topic Name<thead><tbody>p;amp;lt;strong&gt;Section Name </strong&gt;</td>&8

&am
8.1	Area under Simple Curves
8.2	Area between Two Curves

NCERT Solutions for Class 12 Maths Chapter 8 Applications of Integrals – Exercise 8.1

Question 1. Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis.
Solution :

The area of the region bounded by the curve, y2 = x, the lines, x = 1 and x = 4, and the x-axis is the area ABCD.

Question 2. Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
Solution :

The area of the region bounded by the curve, y2 = 9x, x = 2, and x = 4, and the x-axis is the area ABCD.

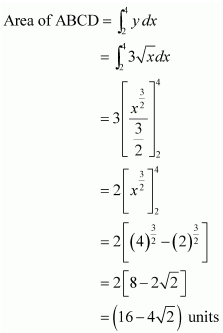
Question 3. Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.

Solution :

The area of the region bounded by the curve, x2 = 4y, y = 2, and y = 4, and the y-axis is the area ABCD.

Question 4. Find the area of the region bounded by the ellipse
Solution :
The given equation of the ellipse, , can be represented as

It can be observed that the ellipse is symmetrical about x-axis and y-axis.

∴ Area bounded by ellipse = 4 × Area of OAB

Therefore, area bounded by the ellipse = 4 × 3π = 12π units

Question 5. Find the area of the region bounded by the ellipse
Solution :

The given equation of the ellipse can be represented as

It can be observed that the ellipse is symmetrical about x-axis and y-axis.

∴ Area bounded by ellipse = 4 × Area OAB

Therefore, area bounded by the ellipse = 4 x3π/2 = 6π units.

Question 6. Find the area of the region in the first quadrant enclosed by x-axis, line x = √3y and the circle x2 + y2 = 4

Solution :
The area of the region bounded by the circle, x2 + y2 = 4,x = √3y and the x-axis is the area OAB.

The point of intersection of the line and the circle in the first quadrant is (√3,1).

Area OAB = Area ΔOCA + Area ACB

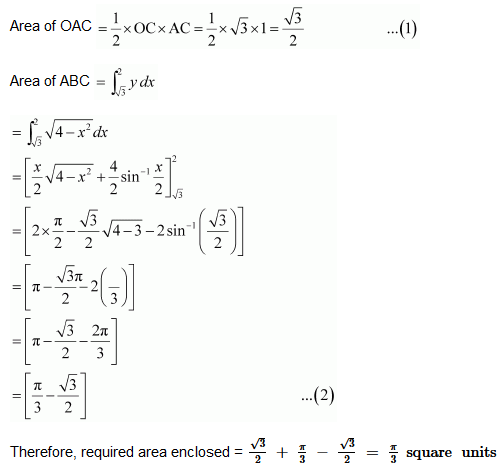
Question 7. Find the area of the smaller part of the circle x2 + y2 = a2 cut off by the line x = a/√2
Solution :

The area of the smaller part of the circle, x2 + y2 = a2, cut off by the line, x = a/√2, is the area ABCDA.

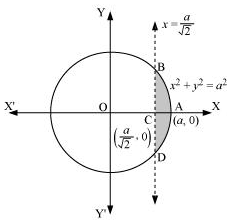
It can be observed that the area ABCD is symmetrical about x-axis.

∴ Area ABCD = 2 × Area ABC

Therefore, the area of smaller part of the circle, x2 + y2 = a2, cut off by the line,

Question8. The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.

Solution :

The line, x = a, divides the area bounded by the parabola and x = 4 into two equal parts.

∴ Area OAD = Area ABCD

It can be observed that the given area is symmetrical about x-axis.

⇒ Area OED = Area EFCD

Question9. Find the area of the region bounded by the parabola y = x2 and y = |x|

Solution :
The area bounded by the parabola, x2 = y,and the line,y = |x|, can be represented as

The given area is symmetrical about y-axis.

∴ Area OACO = Area ODBO

The point of intersection of parabola, x2 = y, and line, y = x, is A (1, 1).

Area of OACO = Area ΔOAM – Area OMACO

Therefore, required area = 2[1/6] = 1/3 units

Question10. Find the area bounded by the curve x2 = 4y and the line x = 4y – 2
Solution : The area bounded by the curve, x2 = 4y, and line, x = 4y – 2, is represented by the shaded area OBAO.

Let A and B be the points of intersection of the line and parabola.

Coordinates of point A are (-1, 1/4).

Coordinates of point B are (2, 1).

We draw AL and BM perpendicular to the x-axis.

It can be observed that,

Area OBAO = Area OBCO + Area OACO … (1)

Then, Area OBCO = Area OMBC – Area OMBO

Similarly, Area OACO = Area OLAC – Area OLAO

Therefore, required area = units

Question11. Find the area of the region bounded by the curve y2 = 4x and the line x = 3

Solution :

The region bounded by the parabola, y2 = 4x, and the line, x = 3, is the area OACO.

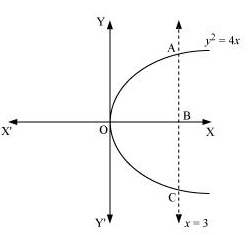
The area OACO is symmetrical about x-axis.

∴ Area of OACO = 2 (Area of OAB)

Therefore, the required area is 8√3 units.

Question12. Choose the correct answer:

Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is

A. π

B. π/2

C. π/3

D. π/4

Solution :

The area bounded by the circle and the lines, x = 0 and x = 2, in the first quadrant is represented as

Therefore, option (A) is correct.

Question13. Choose the correct answer:

Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3 is

A. 2

B. 9/4

C. 9/3

D. 9/2

Solution :
The area bounded by the curve, y2 = 4x, y-axis, and y = 3 is represented as

Therefore, option (B) is correct.

NCERT Solutions for Class 12 Applications of Integrals Chapter 8- Exercise 8.2

Question 1. Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y

Solution :
The required area is represented by the shaded area OBCDO.

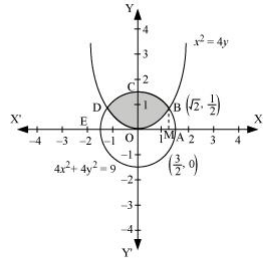
Solving the given equation of circle, 4x2 + 4y2 = 9, and parabola, x2 = 4y, we obtain the point of intersection as B(√2,1/2) and D (-√2,1/2).

It can be observed that the required area is symmetrical about the y-axis.

∴ Area OBCDO = 2 × Area OBCO

We draw BM perpendicular to OA.

Therefore, the coordinates of M are (√2,0).

Therefore, Area OBCO = Area OMBCO – Area OMBO

Therefore, the required area OBCDO is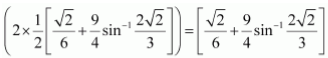

Question 2. Find the area bounded by curves (x – 1)2 + y2 = 1 and x2 + y 2 = 1

Solution :

The area bounded by the curves, (x – 1)2 + y2 = 1 and x2 + y 2 = 1, is represented by the shaded area as

On solving the equations, (x – 1)2 + y2 = 1 and x2 + y 2 = 1, we obtain the point of intersection as A (1/2,√3/2) and B (1/2,√3/2) .

It can be observed that the required area is symmetrical about the x-axis.

∴ Area OBCAO = 2 × Area OCAO

We join AB, which intersects OC at M, such that AM is perpendicular to OC.

The coordinates of M are (1/2,0).

Therefore, required area OBCAO = units.

Question 3. Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3

Solution :

The area bounded by the curves, y = x2 + 2, y = x, x = 0, and x = 3, is represented by the shaded area OCBAO as

Then, Area OCBAO = Area ODBAO – Area ODCO

Question 4. Using integration, find the area of the region bounded by the triangle whose vertices are (–1, 0), (1, 3) and (3, 2).

Solution :

BL and CM are drawn perpendicular to x-axis.

It can be observed in the following figure that,

Area (ΔACB) = Area (ALBA) + Area (BLMCB) – Area (AMCA) … (1)

Therefore, from equation (1), we obtain

Area (ΔABC) = (3 + 5 – 4) = 4 units.

5. Using integration, find the area of the triangular region whose sides have the equations y = 2x +1, y = 3x + 1 and x = 4.

Solution :

The equations of sides of the triangle are y = 2x +1, y = 3x + 1, and x = 4.

On solving these equations, we obtain the vertices of triangle as A(0, 1), B(4, 13), and C (4, 9).

It can be observed that,

Area (ΔACB) = Area (OLBAO) –Area (OLCAO)

Question 6. Choose the correct answer:

Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is

(A)2 (π – 2)

(B). π – 2

(C). 2π – 1

(D). 2 (π + 2)

Solution :

The smaller area enclosed by the circle, x2 + y2 = 4, and the line, x + y = 2, is represented by the shaded area ACBA as

It can be observed that,

Area ACBA = Area OACBO – Area (ΔOAB)

Therefore, option (B) is correct.

Question 7. Choose the correct answer:

Area lying between the curves y2 = 4x and y = 2x is

(A) 2/3

(B) 1/3

(C) 1/4

(D) 3/4

Solution :
The area lying between the curve, y2 = 4x and y = 2x, is represented by the shaded area OBAO as

The points of intersection of these curves are O (0, 0) and A (1, 2).

We draw AC perpendicular to x-axis such that the coordinates of C are (1, 0).

∴ Area OBAO = Area (OCABO) – Area (ΔOCA)

Therefore, option (B) is correct.

NCERT Solutions for Class 12 Applications of Integrals Chapter 8 Miscellaneous Exercise

Question 1. Find the area under the given curves and given lines:

(i) y = x2, x = 1, x = 2 and x-axis

(ii) y = x4, x = 1, x = 5 and x –axis

Solution :
(i)The required area is represented by the shaded area ADCBA as

(ii)The required area is represented by the shaded area ADCBA as

Question 2. Find the area between the curves y = x and y = x2

Solution :

The required area is represented by the shaded area OBAO as

The points of intersection of the curves, y = x and y = x2, is A (1, 1).

We draw AC perpendicular to the x-axis.

∴ Area (OBAO) = Area (ΔOCA) – Area (OCABO) … (1)

Question 3. Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4

Solution : The area in the first quadrant bounded by y = 4x2, x = 0, y = 1, and y = 4 is represented by the shaded area ABCDA as

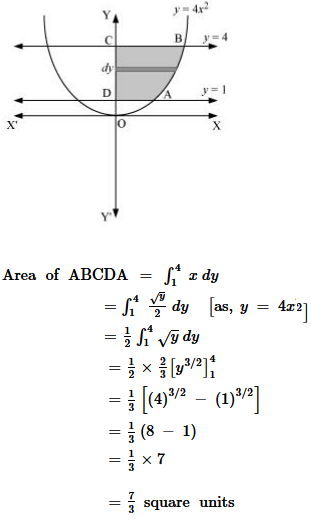
Question 4. Sketch the graph of y = |x + 3| and evaluate

Solution :

The given equation is y = |x + 3|

The corresponding values of x and y are given in the following table.

On plotting these points, we obtain the graph of y = |x + 3| as follows.

Question 5. Find the area bounded by the curve y = sin x between x = 0 and x = 2π

Solution :
The graph of y = sin x can be drawn as

∴ Required area = Area OABO + Area BCDB

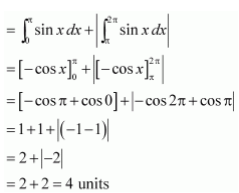
&amp;amp;lt;p><strong>Question 6<</strong>/strong>. Find the area enclosed between the parabola <em>y</</em>em>2 = 4ax</em> and the line y = mxSolution :

The area enclosed between the parabola, y2 = 4ax, and the line, y = mx, is represented by the shaded area OABO as

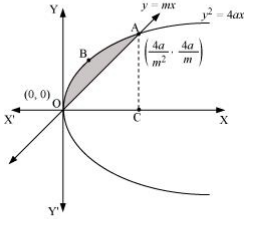
The points of intersection of both the curves are (0, 0) and .

We draw AC perpendicular to the x-axis.

∴ Area OABO = Area OCABO – Area (ΔOCA)

Question 7. Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12

Solution :

The area enclosed between the parabola, 4y = 3x2, and the line, 2y = 3x + 12, is represented by the shaded area OBAO as

The points of intersection of the given curves are A (–2, 3) and (4, 12).

We draw AC and BD perpendicular to x-axis.

∴ Area OBAO = Area CDBA – (Area ODBO + Area OACO)

Question 8. Find the area of the smaller region bounded by the ellipse and the line

Solution :
The area of the smaller region bounded by the ellipse, = 1, and the line, , is represented by the shaded region BCAB as

∴ Area BCAB = Area (OBCAO) – Area (OBAO)

Question 9. Find the area of the smaller region bounded by the ellipse and the line

Solution :
The area of the smaller region bounded by the ellipse, , and the line, , is represented by the shaded region BCAB as

∴ Area BCAB = Area (OBCAO) – Area (OBAO)

Question 10. Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and x-axis

Solution :

The area of the region enclosed by the parabola, x2 = y, the line, y = x + 2, and x-axis is represented by the shaded region OACO as

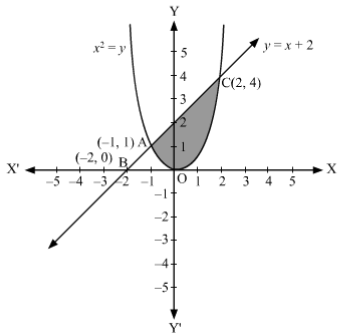
The point of intersection of the parabola, x2 = y, and the line, y = x + 2, is A (–1, 1) and C(2, 4).

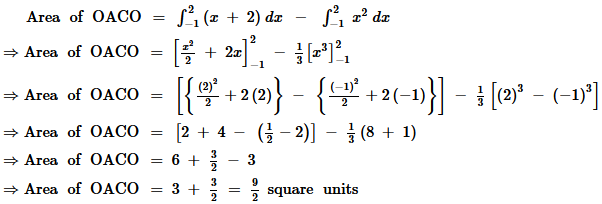
Question 11.Using the method of integration, find the area enclosed by the curve |x| + |y| = 1

[Hint: the required region is bounded by lines x + y = 1, x – y = 1, – x + y = 1 and – x – y = 11]

Solution :
The area bounded by the curve, |x| + |y| = 1, is represented by the shaded region ADCB as

The curve intersects the axes at points A (0, 1), B (1, 0), C (0, –1), and D (–1, 0).

It can be observed that the given curve is symmetrical about x-axis and y-axis.

∴ Area ADCB = 4 × Area OBAO

Question 12. Find the area bounded by curves {(x, y) : y ≥ x2 and y = |x|}.

Solution :
The area bounded by the curves, {(x, y) : y ≥ x2 and y = |x|}., is represented by the shaded region as

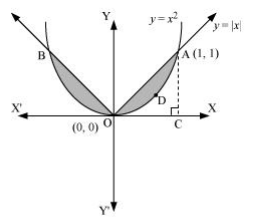
It can be observed that the required area is symmetrical about y-axis.

Question 13.Using the method of integration, find the area of the triangle whose vertices are A (2, 0), B (4, 5) and C (6, 3).

Solution :
Vertices of the given triangle are A (2, 0), B (4, 5) and C (6, 3).

Equation of side AB is

Equation of side BC

Equation of side CA is

Area (ΔABC) = Area (ABLA) + Area (BLMCB) – Area (ACMA)

Question 14.Using the method of integration, find the area of the region bounded by the lines: 2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0

Solution :

The given equations of lines are

2x + y = 4 … (1)

3x – 2y = 6 … (2)

And, x – 3y + 5 = 0 … (3)

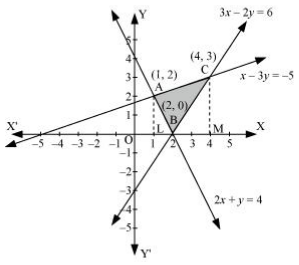
The area of the region bounded by the lines is the area of ΔABC. AL and CM are the perpendiculars on x-axis.

Area (ΔABC) = Area (ALMCA) – Area (ALB) – Area (CMB)

Question 15. Find the area of the region {(x, y) : y2 ≤ 4x, 4×2 + 4y2 ≤ 9}.

Solution :

The area bounded by the curves, {(x, y) : y2 ≤ 4x, 4×2 + 4y2 ≤ 9}, is represented as

The points of intersection of both the curves are (1/2,√2) and (1/2, -√2).

The required area is given by OABCO.

It can be observed that the area OABCO is symmetrical about the x-axis.

∴ Area OABCO = 2 × Area OBC

Area OBCO = Area OMC + Area MBC

Therefore, the required area is units.

Question 16.Choose the correct answer:

Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is

(A) -9

(B) -15/4

(C) 15/4

(D) 17/4

Solution :

Therefore, option (D) is correct.

Question 17.Choose the correct answer:

The area bounded by the curve y = x|x|, axis and the ordinates x = –1 and x = 1 is given by:

[Hint: y = x2 if x > 0 and y = –x2 if x < 0]

(A) 0

(B) 1/3

(C) 2/3

(D) 4/3

Solution :

Therefore, option (C) is correct.

Question 18.Choose the correct answer:

The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is

Solution :

The given equations are

x2 + y2 = 16 … (1)

y2 = 6x … (2)

Area bounded by the circle and parabola

Thus, the correct answer is C.

Question 19.Choose the correct answer:

The area bounded by the y-axis, y = cos x and y = sin x when 0 ≤ x ≤ π/2.

(A) 2(√2 – 1)

(B) √2 – 1

(C) √2 + 1

(D) √2

Solution :

The given equations are

y = cos x … (1)

And, y = sin x … (2)

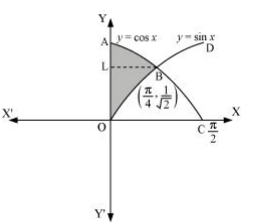
Required area = Area (ABLA) + area (OBLO)

Required area = Area (AB

Therefore, option (B) is correct.