Electric Charges and Fields: NCERT Solutions

NCERT Solutions for Class 12 Physics Chapter 1 Electric Charges and Fields are provided here by SimplyAcad to become a champion of physics. These answers will help to score well in your upcoming board examinations and various entrance exams such as JEE, VITEEE, etc. Our subject experts have prepared the best solutions for your regular practice and revisions. Scroll below to find the answers of Electric Charges and Fields in a structured manner.

Electric Charges and Fields Class 12 Questions 1 to 4

Question 1:

What is the force between two small charged spheres having charges

$2 \times 10^{-7}\,\text{C}$

2×10−7C and

$3 \times 10^{-7}\,\text{C}$

3×10−7C placed 30 cm apart in air?

Solution:

Let the charges be

$q_1 = 2 \times 10^{-7}\,\text{C}$

and

$q_2 = 3 \times 10^{-7}\,\text{C}$

The distance

$d$

between the charges is 0.3m.

Using Coulomb’s law, the force F between the charges is given by:

$$F = \frac{1}{4\pi\epsilon_0} \frac{q_1 q_2}{d^2}$$

Here,

$\frac{1}{4\pi\epsilon_0} = 9 \times 10^9\, \text{N} \cdot \text{m}^2/\text{C}^2$

Substituting the values:

$$F = 9 \times 10^9 \times \frac{(2 \times 10^{-7})(3 \times 10^{-7})}{(0.3)^2}$$

$$F = 9 \times 10^9 \times \frac{6 \times 10^{-14}}{0.09}$$

$$F = 5.994 \times 10^{-3}\,\text{N}$$

 

Since both charges are positive, the force is repulsive.

Question 2:

The electrostatic force on a small sphere of charge

$0.4\,\mu\text{C}$

due to another small sphere of charge −0.8μC in air is 0.2N.

(a) What is the distance between the two spheres?

(b) What is the force on the second sphere due to the first?

Solution:

Given:

$q_1 = 0.4\,\mu\text{C} = 0.4 \times 10^{-6}\,\text{C}$ $q_2 = -0.8\,\mu\text{C} = -0.8 \times 10^{-6}\,\text{C}$ $F = 0.2\,\text{N}$

 

(a) The electrostatic force between the charges is given by Coulomb’s law:

$$F = \frac{1}{4\pi\epsilon_0} \frac{|q_1 q_2|}{r^2}$$

 

Solving for $r$

$$r^2 = \frac{1}{4\pi\epsilon_0} \frac{|q_1 q_2|}{F}$$

$$r^2 = \frac{9 \times 10^9 \times 0.4 \times 10^{-6} \times 0.8 \times 10^{-6}}{0.2}$$

 

$$r^2 = 1.44 \times 10^{-10}\,\text{m}^2$$

$$r = 0.12\,\text{m}$$

The distance between the two spheres is

$0.12\,\text{m}$

(b) By Newton’s third law, the force on the second sphere due to the first is equal in magnitude and opposite in direction. Therefore, the force on the second sphere is also

$0.2\,\text{N}$

 

Question 3:

Check that the ratio

$\frac{k e^2}{G m_e m_p}$

is dimensionless. Look up a Table of Physical Constants and determine the value of this ratio. What does the ratio signify?

Solution:

The given ratio is:

$$\frac{k e^2}{G m_e m_p}$$

Where:

$k = 9 \times 10^9\, \text{N} \cdot \text{m}^2/\text{C}^2$ $e = 1.6 \times 10^{-19}\,\text{C}$ $G = 6.67 \times 10^{-11}\,\text{N} \cdot \text{m}^2/\text{kg}^2$ $m_e = 9.1 \times 10^{-31}\,\text{kg}$ $m_p = 1.66 \times 10^{-27}\,\text{kg}$

Checking the dimensions:

$$\frac{k e^2}{G m_e m_p} = \frac{[\text{N} \cdot \text{m}^2 / \text{C}^2] \times [\text{C}]^2}{[\text{N} \cdot \text{m}^2 / \text{kg}^2] \times [\text{kg}]^2} = 1$$

 

Thus, the ratio is dimensionless.

Substituting the values:

$$\frac{k e^2}{G m_e m_p} = \frac{9 \times 10^9 \times (1.6 \times 10^{-19})^2}{6.67 \times 10^{-11} \times 9.1 \times 10^{-31} \times 1.66 \times 10^{-27}}$$

 

$$= \frac{2.304 \times 10^{-28}}{1.008 \times 10^{-67}} \approx 2.4 \times 10^{39}$$

 

This ratio signifies the strength of the electrostatic force compared to the gravitational force between an electron and a proton, showing that the electrostatic force is much stronger.

Question 4:

(a) Explain the meaning of the statement ‘electric charge of a body is quantized’. (b) Why can one ignore quantization of electric charge when dealing with macroscopic i.e., large scale charges?

Solution:

(a) The statement means that the charge on any object is an integer multiple of the elementary charge

$e = 1.6 \times 10^{-19}\,\text{C}$

e=1.6×10−19C. This means a body can only have charges like

$\pm e, \pm 2e, \pm 3e, \dots$

±e,±2e,±3e,…, and never a fraction of

$e$

(b) On a macroscopic scale, the total charge on objects is so large that the quantization of charge (in units of

$e$

) becomes negligible. For example, when dealing with charges on the order of coulombs, the difference of one or a few elementary charges is insignificant, so the charge can be treated as continuous.

Electric Charges and Fields Class 12 Questions 5 to 8

Question 5:

When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.

Solution:

When a glass rod is rubbed with a silk cloth, electrons are transferred from one to the other due to friction. The glass rod loses electrons and becomes positively charged, while the silk cloth gains those electrons and becomes negatively charged. The total charge remains conserved because the amount of positive charge on the glass rod is equal in magnitude to the negative charge on the silk cloth. This phenomenon is consistent with the law of conservation of charge, which states that the total charge in an isolated system remains constant. Similar phenomena occur with other pairs of materials, where the charges generated are always equal and opposite, ensuring that the total charge remains unchanged.

Question 6:

Four point charges qA=2 μCq_A = 2 \, \mu\text{C}qA​=2μC, qB=−5 μCq_B = -5 \, \mu\text{C}qB​=−5μC, qC=2 μCq_C = 2 \, \mu\text{C}qC​=2μC, and qD=−5 μCq_D = -5 \, \mu\text{C}qD​=−5μC are located at the corners of a square ABCD of 10 cm. What is the force on a charge of 1 μC1 \, \mu\text{C}1μC placed at the center of the square?

Solution:

Given:

• Side of the square AB=BC=CD=DA=10 cm=0.1 mAB = BC = CD = DA = 10 \, \text{cm} = 0.1 \, \text{m}AB=BC=CD=DA=10cm=0.1m
• Charges are qA=2 μCq_A = 2 \, \mu\text{C}qA​=2μC, qB=−5 μCq_B = -5 \, \mu\text{C}qB​=−5μC, qC=2 μCq_C = 2 \, \mu\text{C}qC​=2μC, and qD=−5 μCq_D = -5 \, \mu\text{C}qD​=−5μC.
• Charge at the center OOO of the square is qO=1 μCq_O = 1 \, \mu\text{C}qO​=1μC.

First, calculate the distance from each corner to the center of the square:

• Diagonal of the square AC=BD=2×side=2×0.1=0.141 mAC = BD = \sqrt{2} \times \text{side} = \sqrt{2} \times 0.1 = 0.141 \, \text{m}AC=BD=2​×side=2​×0.1=0.141m.
• Distance from the center to any corner r=Diagonal2=0.1412=0.0705 mr = \frac{\text{Diagonal}}{2} = \frac{0.141}{2} = 0.0705 \, \text{m}r=2Diagonal​=20.141​=0.0705m.

Now, the force between each charge and the charge at the center OOO is:

F=k⋅∣q1⋅q2∣r2F = \frac{k \cdot |q_1 \cdot q_2|}{r^2} F=r2k⋅∣q1​⋅q2​∣​

Where k=8.99×109 N⋅m2/C2k = 8.99 \times 10^9 \, \text{N} \cdot \text{m}^2 / \text{C}^2k=8.99×109N⋅m2/C2.

For qA=2 μCq_A = 2 \, \mu\text{C}qA​=2μC and qO=1 μCq_O = 1 \, \mu\text{C}qO​=1μC:

FA=8.99×109×2×10−6×1×10−6(0.0705)2≈3.62 NF_A = \frac{8.99 \times 10^9 \times 2 \times 10^{-6} \times 1 \times 10^{-6}}{(0.0705)^2} \approx 3.62 \, \text{N}FA​=(0.0705)28.99×109×2×10−6×1×10−6​≈3.62N

Similarly, calculate FBF_BFB​, FCF_CFC​, and FDF_DFD​.

By symmetry and considering the directions, the forces cancel each other out because the forces due to qAq_AqA​ and qCq_CqC​ are equal in magnitude and opposite in direction to the forces due to qBq_BqB​ and qDq_DqD​.

Thus, the net force on the charge at the center of the square is 0 N.

Question 7:

(a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?

Solution:
An electrostatic field line represents the path followed by a positive test charge in an electric field. Since the force on the charge is continuous, the field line must also be continuous without any breaks, reflecting the continuous nature of the force.

(b) Explain why two field lines never cross each other at any point?

Solution:
If two field lines were to cross at a point, it would imply that the electric field has two different directions at that point, which is impossible. The electric field at any point has a unique direction, hence, field lines cannot cross.

Question 8:

Two point charges qA=3 μCq_A = 3 \, \mu\text{C}qA​=3μC and qB=−3 μCq_B = -3 \, \mu\text{C}qB​=−3μC are located 20 cm apart in a vacuum. What is the electric field at the midpoint OOO of the line ABABAB joining the two charges?

Solution:

Given:

• qA=3 μCq_A = 3 \, \mu\text{C}qA​=3μC
• qB=−3 μCq_B = -3 \, \mu\text{C}qB​=−3μC
• Distance AB=20 cm=0.2 mAB = 20 \, \text{cm} = 0.2 \, \text{m}AB=20cm=0.2m
• Midpoint OOO is 0.1 m0.1 \, \text{m}0.1m from each charge.

The electric field due to a point charge at a distance rrr is:

E=k⋅∣q∣r2E = \frac{k \cdot |q|}{r^2}E=r2k⋅∣q∣​

Calculate the electric fields due to qAq_AqA​ and qBq_BqB​ at OOO:

EA=8.99×109×3×10−6(0.1)2=2.7×106 N/CE_A = \frac{8.99 \times 10^9 \times 3 \times 10^{-6}}{(0.1)^2} = 2.7 \times 10^6 \, \text{N/C}EA​=(0.1)28.99×109×3×10−6​=2.7×106N/C EB=8.99×109×3×10−6(0.1)2=2.7×106 N/CE_B = \frac{8.99 \times 10^9 \times 3 \times 10^{-6}}{(0.1)^2} = 2.7 \times 10^6 \, \text{N/C}EB​=(0.1)28.99×109×3×10−6​=2.7×106N/C

Since qAq_AqA​ and qBq_BqB​ have equal magnitude and opposite signs, their fields at OOO will be equal in magnitude but opposite in direction. Therefore, they add up to:

EO=EA+EB=2.7×106+2.7×106=5.4×106 N/CE_O = E_A + E_B = 2.7 \times 10^6 + 2.7 \times 10^6 = 5.4 \times 10^6 \, \text{N/C}EO​=EA​+EB​=2.7×106+2.7×106=5.4×106N/C

The direction of the electric field will be from qBq_BqB​ (negative charge) to qAq_AqA​ (positive charge).

Electric Charges and Fields Class 12 Questions 5 to 8

Question 9:

A system has two charges qA=2.5×10−7 Cq_A = 2.5 \times 10^{-7} \,\text{C}qA​=2.5×10−7C and qB=2.5×10−7 Cq_B = 2.5 \times 10^{-7} \,\text{C}qB​=2.5×10−7C, located at points A:(0,0,−15 cm)A: (0, 0, -15\,\text{cm})A:(0,0,−15cm) and B:(0,0,15 cm)B: (0, 0, 15\,\text{cm})B:(0,0,15cm), respectively. What are the total charge and electric dipole moment of the system?

Solution:

1. Total Charge:
   qtotal=qA+qB=2.5×10−7+2.5×10−7=5×10−7 Cq_{\text{total}} = q_A + q_B = 2.5 \times 10^{-7} + 2.5 \times 10^{-7} = 5 \times 10^{-7} \,\text{C}qtotal​=qA​+qB​=2.5×10−7+2.5×10−7=5×10−7C
2. Electric Dipole Moment: Distance between AAA and BBB:
   d=15 cm−(−15 cm)=30 cm=0.3 md = 15 \, \text{cm} – (-15 \, \text{cm}) = 30 \, \text{cm} = 0.3 \, \text{m}d=15cm−(−15cm)=30cm=0.3m
   Dipole moment:
   p=q×d=2.5×10−7×0.3=7.5×10−8 C⋅mp = q \times d = 2.5 \times 10^{-7} \times 0.3 = 7.5 \times 10^{-8} \,\text{C} \cdot \text{m}p=q×d=2.5×10−7×0.3=7.5×10−8C⋅m
   The dipole moment is directed along the z-axis.

Question 10:

An electric dipole with dipole moment 4×10−9 C⋅m4 \times 10^{-9} \, \text{C} \cdot \text{m}4×10−9C⋅m is aligned at 30∘30^\circ30∘ with the direction of a uniform electric field of magnitude 5×104 N/C5 \times 10^4 \, \text{N/C}5×104N/C. Calculate the magnitude of the torque acting on the dipole.

Solution:

Given:

• p=4×10−9 C⋅mp = 4 \times 10^{-9} \, \text{C} \cdot \text{m}p=4×10−9C⋅m
• θ=30∘\theta = 30^\circθ=30∘
• E=5×104 N/CE = 5 \times 10^4 \, \text{N/C}E=5×104N/C

Torque:

τ=pEsin⁡θ=4×10−9×5×104×sin⁡30∘=10−4 N⋅m\tau = pE \sin \theta = 4 \times 10^{-9} \times 5 \times 10^4 \times \sin 30^\circ = 10^{-4} \, \text{N} \cdot \text{m}τ=pEsinθ=4×10−9×5×104×sin30∘=10−4N⋅m

Question 11:

A polythene piece rubbed with wool is found to have a negative charge of 3×10−7 C3 \times 10^{-7} \, \text{C}3×10−7C.

(a) Estimate the number of electrons transferred (from which to which?).

(b) Is there a transfer of mass from wool to polythene?

Solution:

(a) Number of electrons transferred:

n=qe=3×10−71.6×10−19≈1.87×1012n = \frac{q}{e} = \frac{3 \times 10^{-7}}{1.6 \times 10^{-19}} \approx 1.87 \times 10^{12}n=eq​=1.6×10−193×10−7​≈1.87×1012

Electrons move from wool to polythene.

(b) Transfer of mass:

m=n×me=1.87×1012×9.1×10−31≈1.7×10−18 kgm = n \times m_e = 1.87 \times 10^{12} \times 9.1 \times 10^{-31} \approx 1.7 \times 10^{-18} \, \text{kg}m=n×me​=1.87×1012×9.1×10−31≈1.7×10−18kg

Yes, a small amount of mass is transferred.

Question12. (a) Two insulated charged copper spheres A and B have their centers separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion if the charge on each is 6.5 × 10−7 C? The radii of A and B are negligible compared to the distance of separation.

(b) What is the force of repulsion if each sphere is charged double the above amount, and the distance between them is halved?

Solution :
(a) Charge on sphere A, qA = Charge on sphere B, qB = 6.5 × 10−7 C

Distance between the spheres, r = 50 cm = 0.5 m

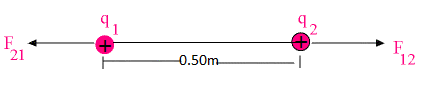
Force of repulsion between the two spheres,

Where,

∈0 = Free space permittivity

= 9 × 109 N m2 C−2

∴

= 1.52 × 10−2 N

Therefore, the force between the two spheres is 1.52 × 10−2 N.

(b) After doubling the charge, charge on sphere A, qA = Charge on sphere B, qB = 2 × 6.5 × 10−7 C = 1.3 × 10−6 C

The distance between the spheres is halved.

∴

Force of repulsion between the two spheres,

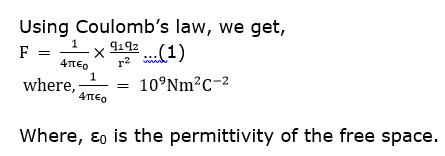
= 16 × 1.52 × 10−2

= 0.243 N

Therefore, the force between the two spheres is 0.243 N.

Electric Charges and Fields Class 12 Questions 13 to 16

Question13. Suppose the spheres A and B in Exercise 1.12 have identical sizes. A third sphere of the same size but uncharged is brought in contact with the first, then brought in contact with the second, and finally removed from both. What is the new force of repulsion between A and B? \textbf

Solution: Let the initial charge on each sphere A and B be \( q = 6.5 \times 10^{-7} \,\text{C} \). The distance between the spheres A and B is \( r = 0.5 \,\text{m} \). 1. **Charge Distribution After Touching Sphere C:** – When the uncharged sphere C is brought in contact with sphere A, the total charge is shared equally between A and C. Therefore, the new charge on each of A and C is: \[ q_A = q_C = \frac{q}{2} = \frac{6.5 \times 10^{-7}}{2} = 3.25 \times 10^{-7} \,\text{C} \] 2. **Charge Distribution After Touching Sphere C with Sphere B:** – Next, sphere C (with charge \( 3.25 \times 10^{-7} \,\text{C} \)) is brought in contact with sphere B (initially with charge \( q = 6.5 \times 10^{-7} \,\text{C} \)). The total charge in this system is: \[ q_B + q_C = 6.5 \times 10^{-7} + 3.25 \times 10^{-7} = 9.75 \times 10^{-7} \,\text{C} \] – When sphere C and B are brought into contact, the total charge is shared equally between them. Therefore, the new charge on each of B and C is: \[ q_B’ = q_C’ = \frac{9.75 \times 10^{-7}}{2} = 4.875 \times 10^{-7} \,\text{C} \] 3. **Final Charge on Sphere A:** – The charge on sphere A remains \( 3.25 \times 10^{-7} \,\text{C} \) after the transfer with C. 4. **Force of Repulsion Between Spheres A and B:** – The force of repulsion \( F \) between two charges is given by Coulomb’s law: \[ F = \frac{1}{4 \pi \epsilon_0} \frac{q_A’ \cdot q_B’}{r^2} \] Substitute the values: \[ F = \frac{9 \times 10^9 \times (3.25 \times 10^{-7}) \times (4.875 \times 10^{-7})}{(0.5)^2} \] \[ F = \frac{9 \times 10^9 \times 15.84375 \times 10^{-14}}{0.25} \] \[ F = \frac{142.5 \times 10^{-5}}{0.25} = 5.703 \times 10^{-3} \,\text{N} \] Therefore, the new force of repulsion between spheres A and B is \( 5.703 \times 10^{-3} \,\text{N} \).

Question14. Figure 1.33 shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge-to-mass ratio? \textbf

{Solution:} From the given figure, we can determine the signs of the charges based on the direction of the deflections: – Particle (1) and Particle (2) both move towards the positive charge. Therefore, both particles are negatively charged. – Since Particle (3) moves towards the negative charge, Particle (3) is positively charged. To find the charge-to-mass ratio, we use the following principles: 1. The force \( F \) on a charged particle in an electric field \( E \) is given by: \[ F = qE \] where \( q \) is the charge of the particle. 2. The force is also given by Newton’s second law: \[ F = ma \] where \( m \) is the mass of the particle and \( a \) is its acceleration. Equating the two expressions for force: \[ qE = ma \] Rearranging for acceleration: \[ a = \frac{qE}{m} \] 3. The deflection \( s \) of the particle in the electric field is given by: \[ s = vt + \frac{1}{2} a t^2 \] where \( v \) is the initial velocity (which is the same for all particles), and \( t \) is the time the particle spends in the field. Substituting the expression for acceleration into the deflection equation: \[ s = vt + \frac{1}{2} \left( \frac{qE}{m} \right) t^2 \] Since \( v \), \( t \), and \( E \) are constants, we have: \[ s \propto \frac{q}{m} \] Therefore, the deflection \( s \) is directly proportional to the charge-to-mass ratio \( \frac{q}{m} \). Given that Particle (3) has the maximum deflection, it will have the highest charge-to-mass ratio. Thus, the charge-to-mass ratio is highest for Particle (3).

Question15. Consider a uniform electric field E = 3 × 103 îN/C. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane? (b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?

Solution :Given:

Electric field E = 3× 103 N/C

Side of square, s = 10 cm

a) Flux of field through square whose plane is parallel to yz plane.

We understand that the normal to the plane is parallel to the direction of field.

So, θ = 0°

Ø = E . A = E × A× cos(θ) …(1)

Where, E = Electric field

A = Area through which we have to calculate flux

θ = Angle between normal to surface and the Electric field

A = s2 = .01 m2

Plugging values, of E, A and θ in equation (1)

Ø = 3× 103 NC-1× 0.01m2× cos0° = 30 Nm2C-1

b) If normal to its (square’s) plane makes 60° with the X axis.

θ = 60° = E × A× cos(θ)

= 3× 103 NC-1× 0.01m2 × cos60° = 15 Nm2C-1

Question16. What is the net flux of the uniform electric field of Exercise 1.15 through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?

Solution : All the faces of a cube are parallel to the coordinate axes. Therefore, the number of field lines entering the cube is equal to the number of field lines piercing out of the cube. As a result, net flux through the cube is zero.

Electric Charges and Fields Class 12 Questions 17 to 20

Question17. Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 × 103 N m2/C. (a) What is the net charge inside the box? (b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or Why not?

Solution :Given:

a) Ø = 8.0× 103 Nm2C-1

Let net charge inside the box = q

We know that,

Flux, Ø = q/ε0 ..(1)

Where, q = net charged enclosed

ε0 = permittivity of free space

ε0 = 8.85× 10-12 N-1 m-2C2

Plugging values of Ø and ε0 in equation (1) we get,

q = Ø × ε0

⇒ q = 8.0 × 103 Nm2C-1× 8.85× 10-12N-1C2m-2

⇒ q = 7.08 × 10-8 C

Hence, the net charge inside the box is 0.07 µC.

(b) No, we cannot conclude that the body doesn’t have any charge. The flux is due to the Net charge of the body. There may still be equal amount of positive and negative charges. So, it is not necessary that if flux is zero then there will be no charges.

Question18. A point charge +10 μC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in Fig. 1.34. What is the magnitude of the electric flux through the square? (Hint: Think of the square as one face of a cube with edge 10 cm.)

Solution :Given:

q = + 10

s = 10 cm

Assume the charge to be enclosed by a cube, where the square is one of its sides.

Now, let us find the total flux through the imaginary cube.

We know that,

Flux, Ø = q/ε …(1)

Where, q = net charged enclosed

ε0 = permittivity of free space

ε0 = 8.85× 10-12 N-1 m-2C2

Now plugging the values of q and ε0 in equation (2)

⇒ Ø = 11.28 × 105 Nm-2C-1

We understand that flux through all the faces of cube will be equal;

Let flux through the square = Øa

Hence,

Øa = Ø/6

Explanation: The net flux will be distributed equally among all 6 faces of the cube. Hence, the square will have one sixth of the total flux.

Øa = 1.88 Nm-2C-1

Question19. A point charge of \(2.0 \, \mu\text{C}\) is at the center of a cubic Gaussian surface with an edge length of \(9.0 \, \text{cm}\). What is the net electric flux through the surface? \textbf

{Solution:} To determine the net electric flux through the cubic Gaussian surface, we use Gauss’s law, which states: \[ \Phi_E = \frac{Q_{\text{enc}}}{\epsilon_0} \] where: – \( \Phi_E \) is the electric flux through the surface, – \( Q_{\text{enc}} \) is the charge enclosed by the surface, – \( \epsilon_0 \) is the permittivity of free space, and its value is \( \epsilon_0 = 8.854 \times 10^{-12} \, \text{F/m} \). Given: – The charge \( Q_{\text{enc}} = 2.0 \, \mu\text{C} = 2.0 \times 10^{-6} \, \text{C} \). Substitute \( Q_{\text{enc}} \) and \( \epsilon_0 \) into Gauss’s law: \[ \Phi_E = \frac{2.0 \times 10^{-6}}{8.854 \times 10^{-12}} \] Perform the calculation: \[ \Phi_E = \frac{2.0 \times 10^{-6}}{8.854 \times 10^{-12}} \approx 2.26 \times 10^5 \, \text{N} \cdot \text{m}^2/\text{C} \] Therefore, the net electric flux through the cubic Gaussian surface is approximately \(2.26 \times 10^5 \, \text{N} \cdot \text{m}^2/\text{C}\).

Question20. A point charge causes an electric flux of \(-1.0 \times 10^3 \, \text{N m}^2/\text{C}\) to pass through a spherical Gaussian surface of \(10.0 \, \text{cm}\) radius centered on the charge. (a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface? (b) What is the value of the point charge? \textbf

{Solution:} Given: – Electric flux, \( \phi = -1.0 \times 10^3 \, \text{N m}^2/\text{C} \) – Radius of Gaussian surface, \( r = 10.0 \, \text{cm} \) (a) The net electric flux through a Gaussian surface is given by Gauss’s law: \[ \phi = \frac{q}{\epsilon_0} \] where: – \( \phi \) is the electric flux, – \( q \) is the charge enclosed by the surface, – \( \epsilon_0 \) is the permittivity of free space, \( \epsilon_0 = 8.854 \times 10^{-12} \, \text{C}^2/\text{N m}^2 \). The electric flux through a Gaussian surface depends only on the charge enclosed and not on the size of the surface. Therefore, if the radius of the Gaussian surface is doubled, the electric flux remains the same. Thus: \[ \phi_{\text{new}} = -1.0 \times 10^3 \, \text{N m}^2/\text{C} \] (b) To find the value of the point charge, use Gauss’s law: \[ \phi = \frac{q}{\epsilon_0} \] Rearrange to solve for \( q \): \[ q = \phi \cdot \epsilon_0 \] Substitute the given values: \[ q = (-1.0 \times 10^3) \times (8.854 \times 10^{-12}) \] \[ q = -8.854 \times 10^{-9} \, \text{C} = -8.854 \, \text{nC} \] Thus, the value of the point charge is \(-8.854 \, \text{nC}\).

Electric Charges and Fields Class 12 Questions 21 to 24

Question21. A uniformly charged conducting sphere has a diameter of \(2.4 \, \text{m}\) and a surface charge density of \(80 \times 10^{-6} \, \text{C/m}^2\). Find the charge on the sphere. \textbf

{Solution:} Given: – Diameter of the sphere, \( D = 2.4 \, \text{m} \) – Surface charge density, \( \sigma = 80 \times 10^{-6} \, \text{C/m}^2 \) First, find the radius \( R \) of the sphere: \[ R = \frac{D}{2} = \frac{2.4}{2} = 1.2 \, \text{m} \] The total charge \( q \) on the sphere can be found using the surface charge density and the surface area of the sphere. The surface area \( A \) of a sphere is given by: \[ A = 4 \pi R^2 \] Substitute the radius into the surface area formula: \[ A = 4 \pi (1.2)^2 \] \[ A = 4 \pi \times 1.44 = 5.76 \pi \, \text{m}^2 \] The charge \( q \) on the sphere is: \[ q = \sigma \times A \] Substitute the values: \[ q = (80 \times 10^{-6}) \times (5.76 \pi) \] \[ q = 80 \times 10^{-6} \times 5.76 \times 3.14 \] \[ q \approx 1.45 \times 10^{-3} \, \text{C} \] Thus, the charge on the sphere is approximately \( 1.45 \times 10^{-3} \, \text{C} \).

Question23. An infinite line charge produces an electric field of \(9 \times 10^4 \, \text{N/C}\) at a distance of \(2 \, \text{cm}\). Calculate the linear charge density. \textbf

{Solution:} Given: – Electric field, \( E = 9 \times 10^4 \, \text{N/C} \) – Distance from the line charge, \( d = 2 \, \text{cm} = 0.02 \, \text{m} \) The electric field \( E \) produced by an infinite line charge with linear charge density \( \lambda \) is given by: \[ E = \frac{\lambda}{2 \pi \epsilon_0 d} \] where: – \( \epsilon_0 \) is the permittivity of free space, \( \epsilon_0 = 8.854 \times 10^{-12} \, \text{C}^2/(\text{N m}^2) \). Rearrange the equation to solve for \( \lambda \): \[ \lambda = E \cdot 2 \pi \epsilon_0 d \] Substitute the given values: \[ \lambda = (9 \times 10^4) \cdot 2 \pi \cdot (8.854 \times 10^{-12}) \cdot 0.02 \] Calculate: \[ \lambda = 9 \times 10^4 \cdot 2 \cdot \pi \cdot 8.854 \times 10^{-12} \cdot 0.02 \] \[ \lambda \approx 9 \times 10^4 \cdot 1.112 \times 10^{-12} \] \[ \lambda \approx 1 \times 10^{-6} \, \text{C/m} \] Thus, the linear charge density is \(1 \, \mu\text{C/m}\).

Question24. Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude \(17.0 \times 10^{-22} \, \text{C/m}^2\). What is \(E\): 1. In the outer region of the first plate? 2. In the outer region of the second plate? 3. Between the plates? \textbf

{Solution:} 1. In the outer region of plate A (region I), the electric field is zero since the charge enclosed by a Gaussian surface in this region is zero. The electric fields due to the two plates are equal in magnitude but opposite in direction in this region. 2. In the outer region of plate B (region III), the electric field is also zero since the charge enclosed by a Gaussian surface in this region is zero. The electric fields due to the two plates are equal in magnitude but opposite in direction in this region. 3. Between the plates (region II), the electric fields add up. Let: – Surface charge density on plate A, \( \sigma_A = +17.0 \times 10^{-22} \, \text{C/m}^2 \) – Surface charge density on plate B, \( \sigma_B = -17.0 \times 10^{-22} \, \text{C/m}^2 \) The net electric field \( E \) between the plates is: \[ E = \frac{\sigma_A}{2 \epsilon_0} + \frac{\sigma_B}{2 \epsilon_0} = \frac{\sigma_A – \sigma_B}{\epsilon_0} \] where \( \epsilon_0 \) is the permittivity of free space, \( \epsilon_0 = 8.854 \times 10^{-12} \, \text{C}^2/(\text{N m}^2) \). Substitute the values: \[ E = \frac{17.0 \times 10^{-22} – (-17.0 \times 10^{-22})}{8.854 \times 10^{-12}} \] \[ E = \frac{34.0 \times 10^{-22}}{8.854 \times 10^{-12}} \] Calculate: \[ E \approx 1.92 \times 10^{-10} \, \text{N/C} \] Thus, the electric field between the plates is \(1.92 \times 10^{-10} \, \text{N/C}\).

Additional Exercises of Electric Charges and Fields Class 12 NCERT Solutions Question 25 to 28

Question25.

An oil drop with 12 excess electrons is held stationary under a constant electric field of 2.55×104 N/C2.55 \times 10^4 \, \text{N/C}2.55×104N/C (Millikan’s oil drop experiment). The density of the oil is 1.26 g/cm31.26 \, \text{g/cm}^31.26g/cm3. Estimate the radius of the drop. (Given: g=9.81 m/s2g = 9.81 \, \text{m/s}^2g=9.81m/s2, e=1.60×10−19 Ce = 1.60 \times 10^{-19} \, \text{C}e=1.60×10−19C).

Solution

Given:

• Electric field, E=2.55×104 N/CE = 2.55 \times 10^4 \, \text{N/C}E=2.55×104N/C
• Density of oil, ρ=1.26 g/cm3=1.26×103 kg/m3\rho = 1.26 \, \text{g/cm}^3 = 1.26 \times 10^3 \, \text{kg/m}^3ρ=1.26g/cm3=1.26×103kg/m3
• Number of excess electrons, n=12n = 12n=12
• Charge of an electron, e=1.60×10−19 Ce = 1.60 \times 10^{-19} \, \text{C}e=1.60×10−19C
• Acceleration due to gravity, g=9.81 m/s2g = 9.81 \, \text{m/s}^2g=9.81m/s2

Calculate the Total Charge of the Oil Drop:

The total charge qqq of the oil drop is given by:

q=n×eq = n \times eq=n×e

Substituting the values:

q=12×1.60×10−19=1.92×10−18 Cq = 12 \times 1.60 \times 10^{-19} = 1.92 \times 10^{-18} \, \text{C}q=12×1.60×10−19=1.92×10−18C

Relate the Weight and Electric Force:

The weight WWW of the oil drop is balanced by the electric force FFF.

The weight WWW of the oil drop is:

W=mgW = mgW=mg

where mmm is the mass of the drop.

The mass mmm is related to the volume VVV of the drop by:

m=V×ρm = V \times \rhom=V×ρ

The volume VVV of the spherical drop is:

V=43πr3V = \frac{4}{3} \pi r^3V=34​πr3

Thus:

m=43πr3×ρm = \frac{4}{3} \pi r^3 \times \rhom=34​πr3×ρ

The weight WWW is then:

W=43πr3ρgW = \frac{4}{3} \pi r^3 \rho gW=34​πr3ρg

Electric Force Acting on the Drop:

The electric force FFF on the drop is:

F=E×qF = E \times qF=E×q

Set Up the Equation for Balance:

Since the weight is balanced by the electric force:

E×q=43πr3ρgE \times q = \frac{4}{3} \pi r^3 \rho gE×q=34​πr3ρg

Rearrange to solve for r3r^3r3:

r3=3E×q4πρgr^3 = \frac{3 E \times q}{4 \pi \rho g}r3=4πρg3E×q​

Substitute the Values:

r3=3×2.55×104×1.92×10−184π×1.26×103×9.81r^3 = \frac{3 \times 2.55 \times 10^4 \times 1.92 \times 10^{-18}}{4 \pi \times 1.26 \times 10^3 \times 9.81}r3=4π×1.26×103×9.813×2.55×104×1.92×10−18​

Calculate:

r3≈1.46976×10−131.5497×104r^3 \approx \frac{1.46976 \times 10^{-13}}{1.5497 \times 10^4}r3≈1.5497×1041.46976×10−13​ r3≈9.48×10−18 m3r^3 \approx 9.48 \times 10^{-18} \, \text{m}^3r3≈9.48×10−18m3

Taking the cube root:

r≈(9.48×10−18)1/3 mr \approx \left(9.48 \times 10^{-18}\right)^{1/3} \, \text{m}r≈(9.48×10−18)1/3m r≈2.1×10−6 m=2.1 μmr \approx 2.1 \times 10^{-6} \, \text{m} = 2.1 \, \mu \text{m}r≈2.1×10−6m=2.1μm

 

Question26. Which among the curves shown in Fig. 1.35 cannot possibly represent electrostatic field lines?

Solution:

(a) Field Lines Not Perpendicular to Conductor:

Reason: Electrostatic field lines must be perpendicular to the surface of a conductor. If the lines are not perpendicular, it suggests that there is a tangential component of the electric field at the surface, which would cause charges to move along the surface. This is not possible in electrostatics as charges at the surface of a conductor are in equilibrium.
Conclusion: The field lines in (a) cannot represent electrostatic field lines.

(b) Field Lines Emerge from Negative and Terminate at Positive:

Reason: Electrostatic field lines always start from positive charges and end on negative charges. They cannot originate from negative charges and terminate on positive charges.
Conclusion: The field lines in (b) cannot represent electrostatic field lines.
(c) Field Lines Emerge from Positive Charges:

Reason: This figure correctly shows field lines emerging from positive charges and spreading out, which is consistent with the behavior of electrostatic fields.
Conclusion: The field lines in (c) correctly represent electrostatic field lines.

(d) Field Lines Intersecting:

Reason: Electrostatic field lines cannot intersect because if they did, it would imply that there are two directions of the electric field at the point of intersection, which is impossible.
Conclusion: The field lines in (d) cannot represent electrostatic field lines.

(e) Field Lines Forming Closed Loops:

Reason: Electrostatic field lines do not form closed loops. They either start from positive charges and end at negative charges or extend to infinity. Closed loops suggest a circulating field, which is not possible in electrostatics.
Conclusion: The field lines in (e) cannot represent electrostatic field lines.

Summary:
(a), (b), (d), and (e): These curves cannot represent electrostatic field lines.
(c): This curve can represent electrostatic field lines.

Question27.

In a certain region of space, the electric field is along the zzz-direction throughout. The magnitude of the electric field is, however, not constant but increases uniformly along the positive zzz-direction at the rate of 105 N/C⋅m−110^5 \, \text{N/C} \cdot \text{m}^{-1}105N/C⋅m−1. What is the torque experienced by an electric dipole in this electric field? The torque experienced by the system is given by: τ=p×E\tau = \mathbf{p} \times \mathbf{E}τ=p×E where p\mathbf{p}p is the dipole moment and E\mathbf{E}E is the electric field.

Solution-

The electric field E\mathbf{E}E varies along the zzz-direction. Let the electric field at position zzz be given by: E(z)=E0+dEdz⋅zE(z) = E_0 + \frac{dE}{dz} \cdot zE(z)=E0​+dzdE​⋅z where E0E_0E0​ is the electric field at z=0z = 0z=0 and dEdz=105 N/C⋅m−1\frac{dE}{dz} = 10^5 \, \text{N/C} \cdot \text{m}^{-1}dzdE​=105N/C⋅m−1 is the rate of increase of the electric field.

The torque τ\tauτ experienced by a dipole p\mathbf{p}p in an electric field E\mathbf{E}E is given by: τ=p×E\tau = \mathbf{p} \times \mathbf{E}τ=p×E

The magnitude of the torque is: τ=pEsin⁡θ\tau = pE \sin \thetaτ=pEsinθ where ppp is the dipole moment, EEE is the magnitude of the electric field, and θ\thetaθ is the angle between the dipole moment and the electric field.

1. When the dipole moment p\mathbf{p}p is aligned with the electric field (θ=0∘\theta = 0^\circθ=0∘):
   In this case, sin⁡θ=sin⁡0∘=0\sin \theta = \sin 0^\circ = 0sinθ=sin0∘=0, so the torque is: τ=pEsin⁡0∘=0\tau = pE \sin 0^\circ = 0τ=pEsin0∘=0 Hence, no torque acts on the dipole when it is aligned with the electric field.
2. When the dipole moment p\mathbf{p}p is aligned opposite to the electric field (θ=180∘\theta = 180^\circθ=180∘):
   In this case, sin⁡θ=sin⁡180∘=0\sin \theta = \sin 180^\circ = 0sinθ=sin180∘=0, so the torque is: τ=pEsin⁡180∘=0\tau = pE \sin 180^\circ = 0τ=pEsin180∘=0 Therefore, the torque is also zero when the dipole is aligned opposite to the electric field.

 

Question28. (a) A conductor A with a cavity as shown in Fig. 1.36(a) is given a charge \(Q\). Show that the entire charge must appear on the outer surface of the conductor. (b) Another conductor B with charge \(q\) is inserted into the cavity keeping B insulated from A. Show that the total charge on the outside surface of A is \(Q + q\) [Fig. 1.36(b)]. (c) A sensitive instrument is to be shielded from the strong electrostatic fields in its environment. Suggest a possible way. \section*

Solution- (a) Consider a Gaussian surface lying wholly within the conductor and enclosing the cavity. Inside the conductor, the electric field intensity is zero. According to Gauss’s law, the electric flux \(\Phi\) through the Gaussian surface is given by: \[ \Phi = \frac{q_{\text{enclosed}}}{\epsilon_0} \] where \(q_{\text{enclosed}}\) is the charge enclosed by the Gaussian surface and \(\epsilon_0\) is the permittivity of free space. Since the electric field inside the conductor is zero, the flux through the Gaussian surface is zero: \[ \Phi = E \cdot ds = 0 \] Thus: \[ \frac{q_{\text{enclosed}}}{\epsilon_0} = 0 \implies q_{\text{enclosed}} = 0 \] Therefore, the entire charge \(Q\) of the conductor must appear on the outer surface of the conductor. (b) When conductor B with charge \(+q\) is inserted into the cavity of conductor A and insulated, it induces a charge of \(-q\) on the inner surface of conductor A. The total charge on the outer surface of conductor A is the sum of its original charge \(Q\) and the charge \(+q\) on the inner surface: \[ Q_{\text{outer}} = Q + q \] Thus, the total charge on the outer surface of conductor A is \(Q + q\). (c) To shield a sensitive instrument from strong electrostatic fields in its environment, the instrument can be enclosed fully inside a metallic surface. A closed metallic body acts as an electrostatic shield by redistributing its charge in such a way that the electric field inside the conductor is zero. This prevents external electric fields from affecting the sensitive instrument inside.

Electric Charges and Fields Class 12 Questions 29 to 32

Question30. Obtain the formula for the electric field due to a long thin wire of uniform linear charge density \(\lambda\) without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral.]

Solution:

Let’s derive the formula for the electric field due to a long thin wire with a uniform linear charge density λ\lambdaλ at a perpendicular distance lll from the wire, without using Gauss’s law.

Consider the Setup

• Let the wire be positioned along the xxx-axis, with a uniform linear charge density λ\lambdaλ.
• We want to find the electric field at a point AAA, located at a perpendicular distance lll from the midpoint OOO of the wire.

Divide the Wire into Differential Elements

• Consider a small element of length dxdxdx on the wire at a distance xxx from the origin OOO.
• The charge of this element is dq=λ dxdq = \lambda \, dxdq=λdx.

Electric Field Due to the Differential Element

• The distance from the differential element dxdxdx to the point AAA is: r=l2+x2r = \sqrt{l^2 + x^2}r=l2+x2​
• The differential electric field dEdEdE at point AAA due to the charge element dqdqdq is given by Coulomb’s law: dE=14πϵ0dqr2=14πϵ0λ dxl2+x2dE = \frac{1}{4 \pi \epsilon_0} \frac{dq}{r^2} = \frac{1}{4 \pi \epsilon_0} \frac{\lambda \, dx}{l^2 + x^2}dE=4πϵ0​1​r2dq​=4πϵ0​1​l2+x2λdx​

Resolve the Electric Field into Components

• The electric field dEdEdE has two components: one parallel to the wire and one perpendicular to the wire.
• Due to symmetry, the parallel components (along the xxx-axis) cancel out when integrated over the entire wire.
• The perpendicular components (along the yyy-axis) add up, so we focus on the perpendicular component: dEperpendicular=dEcos⁡θdE_{\text{perpendicular}} = dE \cos \thetadEperpendicular​=dEcosθ where cos⁡θ=ll2+x2\cos \theta = \frac{l}{\sqrt{l^2 + x^2}}cosθ=l2+x2​l​
• Substituting for dEdEdE: dEperpendicular=14πϵ0λ dxl2+x2⋅ll2+x2=14πϵ0λ l dx(l2+x2)3/2dE_{\text{perpendicular}} = \frac{1}{4 \pi \epsilon_0} \frac{\lambda \, dx}{l^2 + x^2} \cdot \frac{l}{\sqrt{l^2 + x^2}} = \frac{1}{4 \pi \epsilon_0} \frac{\lambda \, l \, dx}{(l^2 + x^2)^{3/2}}dEperpendicular​=4πϵ0​1​l2+x2λdx​⋅l2+x2​l​=4πϵ0​1​(l2+x2)3/2λldx​

Integrate to Find the Total Electric Field

• Integrate dEperpendiculardE_{\text{perpendicular}}dEperpendicular​ over the entire length of the wire: E=∫−∞∞dEperpendicular=∫−∞∞14πϵ0λ l dx(l2+x2)3/2E = \int_{-\infty}^{\infty} dE_{\text{perpendicular}} = \int_{-\infty}^{\infty} \frac{1}{4 \pi \epsilon_0} \frac{\lambda \, l \, dx}{(l^2 + x^2)^{3/2}}E=∫−∞∞​dEperpendicular​=∫−∞∞​4πϵ0​1​(l2+x2)3/2λldx​
• The integral required is a standard form: ∫−∞∞dx(l2+x2)3/2=2l2\int_{-\infty}^{\infty} \frac{dx}{(l^2 + x^2)^{3/2}} = \frac{2}{l^2}∫−∞∞​(l2+x2)3/2dx​=l22​
• Substituting into the expression for EEE: E=14πϵ0λ l⋅2l2=λ2πϵ0lE = \frac{1}{4 \pi \epsilon_0} \lambda \, l \cdot \frac{2}{l^2} = \frac{\lambda}{2 \pi \epsilon_0 l}E=4πϵ0​1​λl⋅l22​=2πϵ0​lλ​

Final Formula

The electric field EEE due to a long thin wire with uniform linear charge density λ\lambdaλ at a perpendicular distance lll from the wire is:

E=λ2πϵ0lE = \frac{\lambda}{2 \pi \epsilon_0 l}E=2πϵ0​lλ​

This result shows that the electric field produced by a long, uniformly charged wire decreases inversely with the distance from the wire.

Question31. It is now believed that protons and neutrons (which constitute nuclei of ordinary matter) are themselves built out of more elementary units called quarks. A proton and a neutron consist of three quarks each. Two types of quarks, the so called ‘up’ quark (denoted by u) of charge (+2/3) e, and the ‘down’ quark (denoted by d) of charge (−1/3) e, together with electrons build up ordinary matter. (Quarks of other types have also been found which give rise to different unusual varieties of matter.) Suggest a possible quark composition of a proton and neutron.

Solution :

Question32. (a) Consider an arbitrary electrostatic field configuration. A small test charge is placed at a null point (i.e., where E = 0) of the configuration. Show that the equilibrium of the test charge is necessarily unstable.

(b) Verify this result for the simple configuration of two charges of the same magnitude and sign placed a certain distance apart.

Solution :
(a) Let the equilibrium of the test charge be stable. If a test charge is in equilibrium and displaced from its position in any direction, then it experiences a restoring force towards a null point, where the electric field is zero. All the field lines near the null point are directed inwards towards the null point. There is a net inward flux of electric field through a closed surface around the null point. According to Gauss’s law, the flux of electric field through a surface, which is not enclosing any charge, is zero. Hence, the equilibrium of the test charge can be stable.

(b) Two charges of same magnitude and same sign are placed at a certain distance. The mid-point of the joining line of the charges is the null point. When a test charged is displaced along the line, it experiences a restoring force. If it is displaced normal to the joining line, then the net force takes it away from the null point. Hence, the charge is unstable because stability of equilibrium requires restoring force in all directions.

Electric Charges and Fields Class 12 Questions 32 to 34

Question33. A particle of mass m and charge (−q) enters the region between the two charged plates initially moving along x-axis with speed vx (like particle 1 in Fig. 1.33). The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is qEL2/ (2mVx2).

Compare this motion with motion of a projectile in gravitational field discussed in Section 4.10 of Class XI Textbook of Physics.

Solution :Given,

Mass of the particle = m

Charge of the particle = -q

Velocity of the particle = vx

Length of the plate = L

Electric field between the plates = E

From Newton’s second law of motion,

This is the vertical displacement of the particle at the far edge of the plate.

This motion is very similar to the motion of a projectile in a gravitational field. In a gravitational field, the force acting on the particle is mg and in the given case it is qE. The trajectory followed by the object will be similar in both the cases.

 

Question34. Suppose that the particle in Exercise 1.33 is an electron projected with velocity \( v_x = 2.0 \times 10^6 \, \text{m/s} \). If the electric field \( E \) between the plates separated by \( 0.5 \, \text{cm} \) is \( 9.1 \times 10^2 \, \text{N/C} \), where will the electron strike the upper plate? (The charge of the electron \( |e| = 1.6 \times 10^{-19} \, \text{C} \), and the mass of the electron \( m_e = 9.1 \times 10^{-31} \, \text{kg} \)). \section*

Solution-

Given:

• Velocity of the electron, vx=2.0×106 m/sv_x = 2.0 \times 10^6 \, \text{m/s}vx​=2.0×106m/s
• Separation between the plates, d=0.5 cm=0.005 md = 0.5 \, \text{cm} = 0.005 \, \text{m}d=0.5cm=0.005m
• Electric field between the plates, E=9.1×102 N/CE = 9.1 \times 10^2 \, \text{N/C}E=9.1×102N/C
• Charge of the electron, ∣e∣=1.6×10−19 C|e| = 1.6 \times 10^{-19} \, \text{C}∣e∣=1.6×10−19C
• Mass of the electron, me=9.1×10−31 kgm_e = 9.1 \times 10^{-31} \, \text{kg}me​=9.1×10−31kg

Step 1: Determine the Acceleration

The force FFF on the electron due to the electric field is given by:

F=qEF = qEF=qE

The acceleration aaa of the electron is then:

a=Fme=qEmea = \frac{F}{m_e} = \frac{qE}{m_e}a=me​F​=me​qE​

Substituting the values:

a=(1.6×10−19 C)×(9.1×102 N/C)9.1×10−31 kg=1.6×1015 m/s2a = \frac{(1.6 \times 10^{-19} \, \text{C}) \times (9.1 \times 10^2 \, \text{N/C})}{9.1 \times 10^{-31} \, \text{kg}} = 1.6 \times 10^{15} \, \text{m/s}^2a=9.1×10−31kg(1.6×10−19C)×(9.1×102N/C)​=1.6×1015m/s2

Step 2: Calculate the Time to Travel the Distance ddd

The time ttt taken by the electron to travel the horizontal distance ddd between the plates is given by:

t=dvxt = \frac{d}{v_x}t=vx​d​

Substituting the values:

t=0.005 m2.0×106 m/s=2.5×10−9 st = \frac{0.005 \, \text{m}}{2.0 \times 10^6 \, \text{m/s}} = 2.5 \times 10^{-9} \, \text{s}t=2.0×106m/s0.005m​=2.5×10−9s

Step 3: Determine the Vertical Displacement sss

The vertical displacement sss is given by the equation of motion:

s=12at2s = \frac{1}{2} a t^2s=21​at2

Substituting the values:

s=12×(1.6×1015 m/s2)×(2.5×10−9 s)2s = \frac{1}{2} \times (1.6 \times 10^{15} \, \text{m/s}^2) \times (2.5 \times 10^{-9} \, \text{s})^2s=21​×(1.6×1015m/s2)×(2.5×10−9s)2 s=12×1.6×1015×6.25×10−18 ms = \frac{1}{2} \times 1.6 \times 10^{15} \times 6.25 \times 10^{-18} \, \text{m}s=21​×1.6×1015×6.25×10−18m s=12×10−2 ms = \frac{1}{2} \times 10^{-2} \, \text{m}s=21​×10−2m s=0.005 m=5 mms = 0.005 \, \text{m} = 5 \, \text{mm}s=0.005m=5mm

Conclusion:

The electron will strike the upper plate after traveling a vertical distance of 5 mm.