Rational Numbers Class 8 – NCERT Solution For Chapter 1

Rational Numbers Class 8 – NCERT Solution For Chapter 1 are given below to help the students ace their examination. The solution focuses on building understanding of the concepts through clear content.These concepts are the building block of every student, therefore students must take it seriously and score well in their exams.

Try to solve different questions after learning the concepts and if stuck in between, then go through the provided solutions.

NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers 1.1

1. Using appropriate properties, find:

(i) -2/3 × 3/5 + 5/2 – 3/5 × 1/6

Solution:

-2/3 × 3/5 + 5/2 – 3/5 × 1/6

= -2/3 × 3/5– 3/5 × 1/6+ 5/2 (by commutativity)

= 3/5 (-2/3 – 1/6)+ 5/2

= 3/5 ((- 4 – 1)/6)+ 5/2

= 3/5 ((–5)/6)+ 5/2 (by distributivity)

= – 15 /30 + 5/2

= – 1 /2 + 5/2

= 4/2

= 2

(ii) 2/5 × (- 3/7) – 1/6 × 3/2 + 1/14 × 2/5

Solution:

2/5 × (- 3/7) – 1/6 × 3/2 + 1/14 × 2/5

= 2/5 × (- 3/7) + 1/14 × 2/5 – (1/6 × 3/2) (by commutativity)

= 2/5 × (- 3/7 + 1/14) – 3/12

= 2/5 × ((- 6 + 1)/14) – 3/12

= 2/5 × ((- 5)/14)) – 1/4

= (-10/70) – 1/4

= – 1/7 – 1/4

= (– 4– 7)/28

= – 11/28

2. Write the additive inverse of each of the following:

Solution:

(i) 2/8

The Additive inverse of 2/8 is – 2/8

(ii) -5/9

The additive inverse of -5/9 is 5/9

(iii) -6/-5 = 6/5

The additive inverse of 6/5 is -6/5

(iv) 2/-9 = -2/9

The additive inverse of -2/9 is 2/9

(v) 19/-16 = -19/16

The additive inverse of -19/16 is 19/16

3. Verify that: -(-x) = x for:

(i) x = 11/15

(ii) x = -13/17

Solution:

(i) x = 11/15

We have, x = 11/15

The additive inverse of x is – x (as x + (-x) = 0).

Then, the additive inverse of 11/15 is – 11/15 (as 11/15 + (-11/15) = 0).

The same equality, 11/15 + (-11/15) = 0, shows that the additive inverse of -11/15 is 11/15.

Or, – (-11/15) = 11/15

i.e., -(-x) = x

(ii) -13/17

We have, x = -13/17

The additive inverse of x is – x (as x + (-x) = 0).

Then, the additive inverse of -13/17 is 13/17 (as 13/17 + (-13/17) = 0).

The same equality (-13/17 + 13/17) = 0, shows that the additive inverse of 13/17 is -13/17.

Or, – (13/17) = -13/17,

i.e., -(-x) = x

4. Find the multiplicative inverse of the following:

(i) -13 (ii) -13/19 (iii) 1/5 (iv) -5/8 × (-3/7) (v) -1 × (-2/5) (vi) -1

Solution:

(i) -13

Multiplicative inverse of -13 is -1/13.

(ii) -13/19

Multiplicative inverse of -13/19 is -19/13.

(iii) 1/5

Multiplicative inverse of 1/5 is 5.

(iv) -5/8 × (-3/7) = 15/56

Multiplicative inverse of 15/56 is 56/15.

(v) -1 × (-2/5) = 2/5

Multiplicative inverse of 2/5 is 5/2.

414

(vi) -1

Multiplicative inverse of -1 is -1.

5. Name the property under multiplication used in each of the following:

(i) -4/5 × 1 = 1 × (-4/5) = -4/5

(ii) -13/17 × (-2/7) = -2/7 × (-13/17)

(iii) -19/29 × 29/-19 = 1

Solution:

(i) -4/5 × 1 = 1 × (-4/5) = -4/5

Here 1 is the multiplicative identity.

(ii) -13/17 × (-2/7) = -2/7 × (-13/17)

The property of commutativity is used in the equation.

(iii) -19/29 × 29/-19 = 1

The multiplicative inverse is the property used in this equation.

6. Multiply 6/13 by the reciprocal of -7/16.

Solution:

Reciprocal of -7/16 = 16/-7 = -16/7

According to the question,

6/13 × (Reciprocal of -7/16)

6/13 × (-16/7) = -96/91

237

7. Tell what property allows you to compute 1/3 × (6 × 4/3) as (1/3 × 6) × 4/3.

Solution:

1/3 × (6 × 4/3) = (1/3 × 6) × 4/3

Here, the way in which factors are grouped in a multiplication problem supposedly does not change the product. Hence, the Associativity Property is used here.

8. Is 8/9 the multiplication inverse of – ? Why or why not?

Solution:

– = -9/8

[Multiplicative inverse ⟹ product should be 1]

According to the question,

8/9 × (-9/8) = -1 ≠ 1

Therefore, 8/9 is not the multiplicative inverse of – .

9. If 0.3 is the multiplicative inverse of
? Why or why not?

Solution:

= 10/3

0.3 = 3/10

[Multiplicative inverse ⟹ product should be 1]

According to the question,

3/10 × 10/3 = 1

Therefore, 0.3 is the multiplicative inverse of 3 1/3

.

10. Write:

(i) The rational number that does not have a reciprocal.

(ii) The rational numbers that are equal to their reciprocals.

(iii) The rational number that is equal to its negative.

Solution:

(I) The rational number that does not have a reciprocal is 0.

Reason:

0 = 0/1

Reciprocal of 0 = 1/0, which is not defined.

137

(ii) The rational numbers that are equal to their reciprocals are 1 and -1.

Reason:

1 = 1/1

Reciprocal of 1 = 1/1 = 1, similarly, reciprocal of -1 = – 1

(iii) The rational number that is equal to its negative is 0.

Reason:

Negative of 0=-0=0

11. Fill in the blanks.

(i) Zero has _______reciprocal.

(ii) The numbers ______and _______are their own reciprocals

(iii) The reciprocal of – 5 is ________.

(iv) Reciprocal of 1/x, where x ≠ 0 is _________.

(v) The product of two rational numbers is always a ________.

(vi) The reciprocal of a positive rational number is _________.

Solution:

(i) Zero has no reciprocal.

(ii) The numbers -1 and 1 are their own reciprocals

(iii) The reciprocal of – 5 is -1/5.

(iv) Reciprocal of 1/x, where x ≠ 0 is x.

(v) The product of two rational numbers is always a rational number.

(vi) The reciprocal of a positive rational number is positive.

NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers 1.2

1. Represent these numbers on the number line.

(i) 7/4

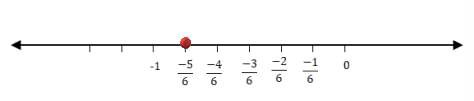
(ii) -5/6

Solution:

(i) 7/4

Divide the line between the whole numbers into 4 parts, i.e. divide the line between 0 and 1 to 4 parts, 1 and 2 to 4 parts, and so on.

Thus, the rational number 7/4 lies at a distance of 7 points away from 0 towards the positive number line.

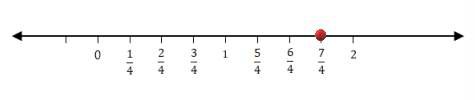
(ii) -5/6

Divide the line between the integers into 4 parts, i.e. divide the line between 0 and -1 to 6 parts, -1 and -2 to 6 parts, and so on. Here, since the numerator is less than the denominator, dividing 0 to – 1 into 6 parts is sufficient.

Thus, the rational number -5/6 lies at a distance of 5 points, away from 0, towards the negative number line.

2. Represent -2/11, -5/11, -9/11 on a number line.

Solution:

Divide the line between the integers into 11 parts.

Thus, the rational numbers -2/11, -5/11, and -9/11 lie at a distance of 2, 5, and 9 points away from 0, towards the negative number line, respectively.

181

3. Write five rational numbers which are smaller than 2.

Solution:

The number 2 can be written as 20/10

Hence, we can say that the five rational numbers which are smaller than 2 are:

2/10, 5/10, 10/10, 15/10, 19/10

4. Find the rational numbers between -2/5 and ½.

Solution:

Let us make the denominators the same, say 50.

-2/5 = (-2 × 10)/(5 × 10) = -20/50

½ = (1 × 25)/(2 × 25) = 25/50

Ten rational numbers between -2/5 and ½ = ten rational numbers between -20/50 and 25/50.

Therefore, ten rational numbers between -20/50 and 25/50 = -18/50, -15/50, -5/50, -2/50, 4/50, 5/50, 8/50, 12/50, 15/50, 20/50.

256

5. Find five rational numbers between:

(i) 2/3 and 4/5

(ii) -3/2 and 5/3

(iii) ¼ and ½

Solution:

(i) 2/3 and 4/5

Let us make the denominators the same, say 60

i.e., 2/3 and 4/5 can be written as:

2/3 = (2 × 20)/(3 × 20) = 40/60

4/5 = (4 × 12)/(5 × 12) = 48/60

Five rational numbers between 2/3 and 4/5 = five rational numbers between 40/60 and 48/60.

Therefore, five rational numbers between 40/60 and 48/60 = 41/60, 42/60, 43/60, 44/60, 45/60.

378

(ii) -3/2 and 5/3

Let us make the denominators the same, say 6

i.e., -3/2 and 5/3 can be written as:

-3/2 = (-3 × 3)/(2× 3) = -9/6

5/3 = (5 × 2)/(3 × 2) = 10/6

Five rational numbers between -3/2 and 5/3 = five rational numbers between -9/6 and 10/6.

Therefore, five rational numbers between -9/6 and 10/6 = -1/6, 2/6, 3/6, 4/6, 5/6.

(iii) ¼ and ½

Let us make the denominators the same, say 24

i.e., ¼ and ½ can be written as:

¼ = (1 × 6)/(4 × 6) = 6/24

½ = (1 × 12)/(2 × 12) = 12/24

Five rational numbers between ¼ and ½ = five rational numbers between 6/24 and 12/24.

Therefore, five rational numbers between 6/24 and 12/24 = 7/24, 8/24, 9/24, 10/24, 11/24.

6. Write five rational numbers greater than -2.

Solution:

-2 can be written as – 20/10

Hence, we can say that the five rational numbers greater than -2 are

-10/10, -5/10, -1/10, 5/10, 7/10

7. Find ten rational numbers between 3/5 and ¾.

Solution:

Let us make the denominators the same, say 80.

3/5 = (3 × 16)/(5× 16) = 48/80

3/4 = (3 × 20)/(4 × 20) = 60/80

Ten rational numbers between 3/5 and ¾ = ten rational numbers between 48/80 and 60/80.

Therefore, ten rational numbers between 48/80 and 60/80 = 49/80, 50/80, 51/80, 52/80, 54/80, 55/80, 56/80, 57/80, 58/80, 59/80.

NCERT Solutions for Class 8 Maths Chapter 1 Rational Numbers Summary

Chapter 1, Rational Numbers comprises 2 exercises, and the NCERT Solutions for Class 8 Maths given here contains precise answers for all the questions present in these exercises. Let us have a look at some of the concepts that are being discussed in this chapter.

• Rational numbers are closed under the operations of addition, subtraction and multiplication.
• The operations of addition and multiplication are as follows:
  • Commutative for rational numbers
  • Associative for rational numbers
• The rational number 0 is the additive identity for rational numbers.
• Rational number 1 is the multiplicative identity for rational numbers.
• Distributivity of rational numbers: For all rational numbers a, b and c, a(b + c) = ab + ac and a(b – c) = ab – ac
• Rational numbers can be represented on a number line.
• Between any two given rational numbers, there are countless rational numbers. The idea of meaning helps us to find rational numbers between two rational numbers.