NCERT Solutions for Class 8 Maths Chapter 11 Direct and Inverse Proportions
Direct and Inverse Proportions – NCERT Solutions for Class 8
SimplyAcad brings you free solved questions of all the exercises in your NCERT Solutions for Class 8 Maths Chapter 11 Direct and Inverse Proportions
The solutions are explained in a detailed way and ensure clarity for better understanding of the concepts. Using these solutions, students can boost their mathematics game and master up their skill. Go below to find all the answers with exact questions in your NCERT book.
NCERT Solutions for Class 8 Maths Chapter 11 Direct and Inverse Proportions Exercise 11.1
1. Following are the car parking charges near a railway station. Check if the parking charges are in direct proportion to the parking time.
Solution- To check the direct proportion, we will find out the ratios of the parking charge and parking time altogether. If two ratios are equivalent to each other, then they are said to be in proportion. Let’s take the first two cases: \begin{align*} \text{Case 1:} & \quad \text{Charge} = 60, \, \text{Time} = 4 \\ \text{Case 2:} & \quad \text{Charge} = 100, \, \text{Time} = 8 \end{align*} On simplifying, we get: \begin{align*} \text{Case 1 ratio} &= \frac{60}{4} = 15 \, \text{rupees per hour} \\ \text{Case 2 ratio} &= \frac{100}{8} = 12.5 \, \text{rupees per hour} \end{align*} Here, both ratios are not the same, so the parking charges are not in direct proportion to the parking time.
2. A mixture of paint is prepared by mixing 1 part of red pigment with 8 parts of base. In the following table, find the parts of base that need to be added. \section*
Solution- While mixing, the ratio of pigment and base should be the same. As parts of pigment increase, the parts of base will also increase. Hence, it is a case of direct proportion. We have the red pigment to base ratio given as \( 1 : 8 \). Let the part of base be \( x \). \begin{itemize} \item[(a)] For red pigment equal to 4: \begin{align*} \frac{1}{8} &= \frac{4}{x} \\ x &= 8 \times 4 = 32 \end{align*} \item[(b)] For red pigment equal to 7: \begin{align*} \frac{1}{8} &= \frac{7}{x} \\ x &= 8 \times 7 = 56 \end{align*} \item[(c)] For red pigment equal to 12: \begin{align*} \frac{1}{8} &= \frac{12}{x} \\ x &= 8 \times 12 = 96 \end{align*} \item[(d)] For red pigment equal to 20: \begin{align*} \frac{1}{8} &= \frac{20}{x} \\ x &= 8 \times 20 = 160
3. If \(\frac{1}{n}\) part of a red pigment requires \(\frac{m}{n}\) of base, how much red pigment should we mix with \(\frac{p}{n}\) of base? \section*
Solution- Finding the required quantity of red pigment: The quantity of red pigment required is directly proportional to the quantity of the base. Let the parts of red pigment required for \(\frac{p}{n}\) be \(x\). \(\frac{1}{n}\) part of red pigment : \(\frac{m}{n}\) of base \(x\) part of red pigment : \(\frac{p}{n}\) of base Setting up the proportion: \[ \frac{\frac{1}{n}}{\frac{m}{n}} = \frac{x}{\frac{p}{n}} \] Solving for \(x\): \[ \frac{1}{m} = \frac{x}{p} \] \[ x = \frac{p}{m} \] Hence, \(\frac{p}{m}\) parts of red pigment are required for \(\frac{p}{n}\) of base.
4. A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours? \section*
Solution – Let the machine fill \( x \) bottles in five hours. The number of bottles filled is directly proportional to the number of hours the machine operates. Thus, we can set up the proportion: \[ \frac{840}{6} = \frac{x}{5} \] Solving for \( x \): \[ x = \frac{840 \times 5}{6} \] \[ x = 700 \text{ bottles} \] Hence, the machine will fill 700 bottles in five hours.
5. A photograph of a bacterium enlarged 50,000 times attains a length of 5 cm. What is the actual length of the bacterium? If the photograph is enlarged 20,000 times only, what would be its enlarged length? \section*
{Solution} Let the actual length of the bacterium be \( x \) cm, and the enlarged length of the bacterium be \( y \) cm if the photograph is enlarged 20,000 times. The given information can be summarized as follows: \[ \begin{array}{c|c|c|c} \text{Length of bacterium (in cm)} & 5 & x & y \\ \hline \text{Number of times photograph of bacterium was enlarged} & 50000 & 1 & 20000 \\ \end{array} \] The number of times the photograph of the bacterium was enlarged and the length of the bacterium are in direct proportion. Therefore, we obtain: \[ \frac{5}{50000} = \frac{x}{1} \] Solving for \( x \): \[ x = \frac{5}{50000} \] \[ x = 10^{-4} \text{ cm} \] Hence, the actual length of the bacterium is \( 10^{-4} \) cm. Now, let the length of the bacterium when the photograph is enlarged 20,000 times be \( y \). We have: \[ \frac{5}{50000} = \frac{y}{20000} \] Solving for \( y \): \[ y = \frac{5 \times 20000}{50000} \] \[ y = 2 \text{ cm} \] Hence, the enlarged length of the bacterium is 2 cm.
6. In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship?
Solution:
Let the length of the model ship be x.
| Length of Actual Ship in m | Length of model ship in cm |
| 12 | 9 |
| 28 | x |
Here, the length of the mast and the actual length of the ship are in direct proportion.
12/9 = 28/ x
→ x*12 = 28*9
→ x = 28*9/12
x = 21 cm
Hence, the length of the model ship is 21 cm.
7. Suppose 2 kg of sugar contains 9×106 crystals. How many sugar crystals are there in
(i) 5 kg of sugar? (ii) 1.2 kg of sugar?
Solution:
(i) Let sugar crystals be x.

| Weight of sugar in kg | No of crystal |
| 2 | 9*106 |
| 5 | x |
Here, the weight of sugar and the number of crystals are in direct proportion.
2→ 9*106
5 → x
2/9*106 = 5/x
→ x*2 = 5*9*106
X = 45/2 *106
→ 22.5*106 → 2.25*107
Hence, the number of sugar crystals is 2.25*107
(ii) Let sugar crystals be x.
Here, the weight of sugar and the number of crystals are in direct proportion.
| Weight of sugar in kg | No of crystal |
| 2 | 9*106 |
| 1.2 | x |
2→ 9*106
1.2 → x
2/9*106 = 1.2/x
→ x*2 = 1.2*9*106
X = 0.6 * 9*106 = 5.4 *106
Hence, the number of sugar crystals is 5.4×106.
8. Rashmi has a road map with a scale of 1 cm representing 18 km. She drives on the road for 72 km. What would be her distance covered on the map?
Solution:
Let the distance covered in the map be x.
| Actual Distance in Km | Distance Covered in map in cm |
| 18 | 1 |
| 72 | x |
Here, the actual distance and distance covered in the map are in direct proportion.
18/1 = 72/x
→ x*18 = 72*1
X = 72*1/18
x = 4 cm
Hence, the distance covered on the map is 4 cm.
9. A 5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time (i) the length of the shadow cast by another pole 10 m 50 cm high (ii) the height of a pole which casts a shadow 5 m long.
Solution:
Here, the height of the pole and the length of the shadow are in direct proportion.
And 1 m = 100 cm
5 m 60 cm = 5×100+60 = 560 cm
3 m 20 cm = 3×100+20 = 320 cm
10 m 50 cm = 10×100+50 = 1050 cm
5 m = 5×100 = 500 cm
(i) Let the length of the shadow of another pole be x.
| Height of pole in cm | Length of shadow in cm |
| 560 | 320 |
| 1050 | x |
560 → 320
1050 → x
560/320 = 1050/x
x*560 = 1050*320
x= 1050*320/560
x= 600 cm = 6m
Hence, the length of the shadow of another pole is 6 m.
(ii) Let the height of the pole be x.
| Height of pole in cm | Length of shadow in cm |
| 560 | 320 |
| x | 500 |
560 → 320
X → 500
560/320 = x/500
→ x*320 = 560*500
X = 560*500/320
X = 875 →
= 875 cm = 8 m 75 cm
Hence, the height of the pole is 8 m 75 cm.
10. A loaded truck travels 14 km in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?
Solution:
Let the distance covered in 5 hours be x km.
1 hour = 60 minutes
Therefore, 5 hours = 5×60 = 300 minutes
| Distance in km | Time in minutes |
| 14 | 25 |
| X | 300 |
Here, the distance covered and time are in direct proportion.
14 —> 25
X —> 300
14/25 = x/300
→ 25x = 300(14)
x = 168
Therefore, the truck can travel 168 km in 5 hours.
NCERT Solutions for Class 8 Maths Chapter 11 Direct and Inverse Proportions Exercise 11.2
1. Which of the following are in inverse proportion?
(i) The number of workers on a job and the time to complete the job.
(ii) The time taken for a journey and the distance travelled at a uniform speed.
(iii) Area of cultivated land and the crop harvested.
(iv) The time taken for a fixed journey and the speed of the vehicle.
(v) The population of a country and the area of land per person.
Solution:
(i) The number of workers and the time to complete the job is in inverse proportion because less workers will take more time to complete a job, and more workers will take less time to complete the same job.
(ii) Time and distance covered in direct proportion.
(iii) It is a direct proportion because more are of cultivated land will yield more crops.
(iv) Time and speed are in inverse proportion because if time is less, speed is more.
(v) It is an inverse proportion. If the population of a country increases, the area of land per person decreases.
2. In a Television game show, the prize money of Rs.1,00,000 is to be divided equally amongst the winners. Complete the following table and find whether the prize money given to an individual winner is directly or inversely proportional to the number of winners:

Solution:
Here, the number of winners and prize money are in inverse proportion because winners are increasing, and prize money is decreasing.
When the number of winners is 4, each winner will get =100000/4 = Rs. 25,000
When the number of winners is 5, each winner will get =100000/5 = Rs. 20,000
When the number of winners is 8, each winner will get =100000/8 = Rs. 12,500
When the number of winners is 10, each winner will get = 100000/10 = Rs. 10,000
When the number of winners is 20, each winner will get = 100000/20 = Rs. 5,000
3. Rehman is making a wheel using spokes. He wants to fix equal spokes in such a way that the angles between any pair of consecutive spokes are equal. Help him by completing the following table:
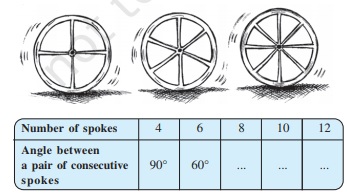
(i) Are the number of spokes and the angles formed between the pairs of consecutive spokes in inverse proportion?
(ii) Calculate the angle between a pair of consecutive spokes on a wheel with 15 spokes.
(iii) How many spokes would be needed, if the angle between a pair of consecutive spokes is 40 degree?
Solution:
Here, the number of spokes is increasing, and the angle between a pair of consecutive spokes is decreasing. So, it is an inverse proportion, and the angle at the centre of a circle is 360 degree.
When the number of spokes is 8, then the angle between a pair of consecutive spokes = 360/8 = 45 degree
When the number of spokes is 10, then the angle between a pair of consecutive spokes = 360/10= 36 degree.
When the number of spokes is 12, then the angle between a pair of consecutive spokes = 360/12 = 30 degree.
| No of spokes | Angles between a pair of consecutive spokes |
| 4 | 90o |
| 6 | 60o |
| 8 | 45o |
| 10 | 36o |
| 12 | 30o |
(i) Yes, the number of spokes and the angles formed between a pair of consecutive spokes is in inverse proportion.
(ii) When the number of spokes is 15, then the angle between a pair of consecutive spokes = 360/15= 24 degree.
(iii) The number of spokes would be needed = 360/40 = 9
4. If a box of sweets is divided among 24 children, they will get 5 sweets each. How many would each get, if the number of children is reduced by 4?
Solution:
Each child gets = 5 sweets
24 children will get 24×5 = 120 sweets.
Total number of sweets = 120
If the number of children is reduced by 4, then children left = 24-4 = 20
Now, each child will get sweets = 120/20 = 6 sweets
5. A farmer has enough food to feed 20 animals in his cattle for 6 days. How long would the food last if there were 10 more animals in his cattle?
Solution:
Let the number of days be x.
Total number of animals = 20+10 = 30
| Animals | Days |
| 20 | 6 |
| 30 | x |
Here, the number of animals and the number of days are in inverse proportion.
30 * x = 20*6
x = 20*6/30
x = 4
Hence, the food will last for four days.
6. A contractor estimates that 3 persons could rewire Jasminder’s house in 4 days. If he uses 4 persons instead of three, how long should they take to complete the job?
Solution:
Let the time taken to complete the job be x.
| Person | Days |
| 3 | 4 |
| 4 | x |
Here, the number of persons and the number of days are in inverse proportion.
¾ = x/4
3×4 = 4x
x = 3×4/4
x = 3
Hence, 4 persons will complete the job in 3 days.
7. A batch of bottles was packed in 25 boxes, with 12 bottles in each box. If the same batch is packed using 20 bottles in each box, how many boxes would be filled?
Solution:
Let the number of boxes be x.
| No of bottles in each box | Boxes |
| 12 | 25 |
| 20 | X |
Here, the number of bottles and the number of boxes are in inverse proportion.
12/20 = x/25
12×25 = 20x
x = 12×25/20 = 15
Hence, 15 boxes would be filled.
8. A factory requires 42 machines to produce a given number of articles in 63 days. How many machines would be required to produce the same number of articles in 54 days?
Solution:
Let the number of machines required be x.
| Machines | Days |
| 42 | 63 |
| x | 42 |
Here, the number of machines and the number of days are in inverse proportion.
63/54 = x/42
63×42 = 54x
x = 63×42/54
x= 49
Hence, 49 machines would be required.
9. A car takes 2 hours to reach a destination by travelling at the speed of 60 km/hr. How long will it take when the car travels at the speed of 80 km/hr?
Solution :
Let the number of hours be x.
| Speed (Km/hour) | Time (hour) |
| 60 | 2 |
| 80 | x |
Here, the speed of the car and time are in inverse proportion.
60/80 = x/2
60×2 = 80x
x = 60×2/80
x= 3/2 = 1.5 hours
Hence the car will take 1 hour 30 minutes to reach its destination
10. Two persons could fit new windows in a house in 3 days.
(i) One of the persons fell ill before the work started. How long would the job take now?
(ii) How many persons would be needed to fit the windows in one day?
Solution:
(i) Let the number of days be x.
| Person | Days |
| 2 | 1 |
| 3 | x |
Here, the number of persons and the number of days are in inverse proportion.
2/1 = x/3
6 = x
Or
x = 6 days
(ii) Let the number of persons be x.
| Person | Days |
| 3 | 1 |
| 2 | x |
Here, the number of persons and the number of days are in inverse proportion.
2/x = 1/3
6 = x
Or
x = 6 persons
11. A school has 8 periods a day, each of 45 minutes duration. How long would each period be, if the school has 9 periods a day, assuming the number of school hours to be the same?
Solution:
Let the duration of each period be x.
| Periods | Duration of period |
| 8 | 45 |
| 9 | x |
Here, the number of periods and the duration of periods are in inverse proportion.
8/9 = x/45
8×45 = 9x
x = 40
Hence, the duration of each period would be 40 minutes.
latest video
news via inbox
Nulla turp dis cursus. Integer liberos euismod pretium faucibua





