Force And Law Of Motion NCERT Solutions

The NCERT Solutions for Class 9 Science Chapter 8 Force and Laws Of Motion is provided here by SimplyAcad to help students gain in-depth knowledge of the concepts discussed. Students can use the availed study material as a guide to answer different types of questions asked in the paper. These solutions are comprehensive and easy to understand promising students great aid in their coming exams. Scroll below to view the answers of Force And Law Of Motion and regularly practise them.

 

 

Access NCERT Solutions for Class 9 Science Chapter 8 Force and Laws Of Motion

Question 1.An object has moved through a distance. Can it have zero displacement? If yes, support your answer with an example.

Solution : Yes, if an object has moved through a distance it can have zero displacement because displacement of an object is the actual change in its position when it moves from one position to the other. So if an object travels from point A to B and then returns back to point A again, the total displacement is zero.

Question 2. A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds?

Solution :

Distance covered by farmer in 40 seconds

=4 x(10) m= 40 m

Speed of the farmer = distance/time = 40m/40s = 1 m/s.

Total time given in the Question = 2min 20seconds

= 60+60+20 =140 seconds

Since he completes 1round of the field in 40seconds so in he will complete 3rounds in 120seconds (2mins) or 120m distance is covered in 2minutes. In another 20seconds will cover another 20m so total distance covered in 2min20sec

= 120 +20 =140m.

Displacement = √102 + 102 =√200

= 10√ m (as per diagram)

=10 x 1.414= 14.14 m.

Question 3. Which of the following is true for displacement?
(a) It cannot be zero.
(b) Its magnitude is greater than the distance travelled by the object.

Solution : Both (a) as well as (b) are false with respect to concept of displacement.

Question 4. Distinguish between speed and velocity.

Solution : Speed of a body is the distance travelled by it per unit time while velocity is displacement per unit time of the body during movement.

Question 5.Under what condition(s) is the magnitude of average velocity of an object equal to its average speed?
Solution : If distance travelled by an object is equal to its displacement then the magnitude of average velocity of an object will be equal to its average speed.

Question 6. What does the odometer of an automobile measure?
Solution : The odometer of an automobile measures the distance covered by that automobile.

Question 7. What does the path of an object look like when it is in uniform motion?
Solution : Graphically the path of an object will be linear i.e. look like a straight line when it is in uniform motion.

Question 8. During an experiment, a signal from a spaceship reached the ground station in five minutes. What was the distance of the spaceship from the ground station? The signal travels at the speed of light, that is 3 x108ms-1
Solution :

Distance = Speed x time

=

=

Question 9. When will you say a body is in
(i) uniform acceleration?
(ii) non-uniform acceleration?
Solution :

(i) uniform acceleration: When an object travels in a straight line and its velocity changes by equal amount in equal intervals of time, it is said to have uniform acceleration.

(ii) non uniform acceleration: It is also called variable acceleration. When the velocity of an object changes by unequal amounts in equal intervals of time, it is said to have non uniform acceleration.

Question 10. A bus decreases its speed from 80kmh-1 to 60km h-1 in 5 s. Find the acceleration of the bus.

Solution :

Initial speed of bus (u) =

= = =

final speed of bus (v)= =

=

= time (t) = 5 s

acceleration (a) = ( v – u) /t = (16.67 – 22.22)/5 = -5.55/5 =

Question 11. A train starting from a railway station and moving with uniform acceleration attains a speed 40km h-1 in 10 minutes. Find its acceleration.

Solution : Since the train starts from rest(railway station) = u = zero

Final velocity of train

=

time (t) = 10 min = 10 x 60

= 600 seconds

Since a = (v – u )/t =

=

Question 12. What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?

Solution : If an object has a uniform motion then the nature of distance time graph will be linear i.e. it would a straight line and if it has non uniform motion then the nature of distance time graph is a curved line.

Question 13. What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis? \textbf

{Solution:} A distance-time graph that is a straight line parallel to the time axis indicates that the object is at rest. This is because: \begin{itemize} \item In a distance-time graph, the distance covered by the object is plotted on the vertical axis, and time is plotted on the horizontal axis. \item A straight line parallel to the time axis means that the distance remains constant regardless of the passage of time. \item Since the distance does not change over time, the object is not moving; it is stationary. \end{itemize} \begin{center} % Drawing a sample distance-time graph

Question 14.What can you say about the motion of an object if its speed-time graph is a straight line parallel to the time axis? \textbf

{Solution:} If the speed-time graph of an object is a straight line parallel to the time axis, it indicates that the object is in uniform motion. This is because: \begin{itemize} \item In a speed-time graph, speed is plotted on the vertical axis, and time is plotted on the horizontal axis. \item A straight line parallel to the time axis means that the speed remains constant regardless of the passage of time. \item Since the speed does not change, the object is moving with a constant velocity. \item Uniform motion is characterized by constant speed and direction, meaning the object is in a state of steady motion without acceleration or deceleration. \end{itemize} \begin{center} % Drawing a sample speed-time graph \includegraphics[width=0.6\textwidth]

Question 15. What is the quantity which is measured by the area occupied below the velocity-time graph?
Solution : The area occupied below the velocity-time graph measures the distance moved by any object.

Question 16. A bus starting from rest moves with a uniform acceleration of 0.1m s-2 for 2 minutes. Find (a)the speed acquired, (b) the distance travelled.
Solution :

(a) u=o, , t= 2min = 120 seconds.

v=u+at

so (a) speed acquired

=

(b)

= 720 m.

Question 17. A train is travelling at a speed of 90km h-1. Brakes are applied so as to produce a uniform acceleration of -0.5m s-2. Find how far the train will go before it is brought to rest.
Solution :

,

v =0(train is brought to rest)

v= u+at

0 =25 – 0.5 x

0.5t = 25, or t

= 25/0.5

= 50seconds

= 1250 – 625 = 625m

Question 18. A trolley, while going down an inclined plane, has an acceleration of 2cm s-2 . What will be its velocity 3 s after the start?
Solution :

, t= 3s

v= u +at = 0 + 2 x 3 = 6 cm/s

Question 19. A racing car has a uniform acceleration of 4cm s-2. What distance will it cover in 10 s after start?
Solution :

u = 0, , t= 10 s

= 200 m

Question 20. A stone is thrown in a vertically upward direction with a velocity of 5 cm s-2. If the acceleration of the stone during its motion is 10 cm s-2n the downward direction, what will be the height attained by the stone and how much time will it take to reach there?
Solution :

v = 0 (since at maximum height its velocity will be zero)

v = u + at

= 5 + (-10) x t

0 = 5 – 10t

10t = 5, or, t = 5/10 =0.5second.

= 2.5 – 1.25 = 1.25m

Question 21. An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 minutes 20 s?
Solution :

circumference of circular track = 2πr

= 4400/7 m

rounds completed by athlete in

2min20sec = s= 140/40 = 3.5

therefore, total distance covered =4400 / 7 x 3.5= 2200 m

Since one complete round of circular track needs 40s so he will complete 3 rounds in 2 mins and in next 20s he can complete half a round therefore displacement = diameter = 200m.

Question 22. Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 50 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging (a) from A to B and (b) from A to C?

Solution :

(a) distance = 300m

time = 2min30seconds = 150 seconds

average speed from A to B = average velocity from A to B

= 300m/150s = 2m/s

(b) average speed from A to C = (300+100)m/(150+60)sec

= 400m/210s = 1.90m/s

displacement from A to C

= (300 – 100)m =200m

time =2min30sec + 1min = 210s

velocity = displacement/time

= 200m/210s = 0.95m/s

Question 23. Abdul, while driving to school, computes the average speed for his trip to be 20km h-1. On his return trip along the same route, there is less traffic and the average speed is 40km h-1. What is the average speed for Abdul’s trip?

Solution :

If we suppose that distance from Abdul’s home to school = x kms

while driving to school :-

,

velocity = displacement/time

20 = x/t, or, t=x/20 hr

on his return trip :-

speed = 40 km h–1 ,

40= x /t’

or, t’ =x/40 hr

total distance travelled = x + x = 2x

total time = t + t’ = x/20 + x/40

=(2x + x)/40 = 3x/40 hr

average speed for Abdul’s trip

= 2x/(3x/40) = 80x/3x = 26.67km/hr

Question 24. A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0 m s-2 for 8.0 s. How far does the boat travel during this time?
Solution :

since the motorboat starts from rest so u= 0

time (t) = 8s,

distance

= 96m

Question 25. A driver of a car travelling at 52 km h-1 applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 s. Another driver going at 3 km h-1 in another car applies his brakes slowly and stops in 10 s. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied?

Solution :

As given in the figure below AB (in red line) and CD(in red line) are the Speed-time graph for given two cars with initial speeds respectively.

Distance Travelled by first car before coming to rest =Area of

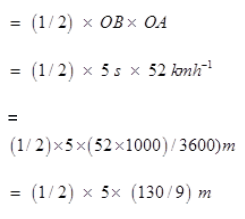
= 325/9 m

= 36.11 m

Distance Travelled by second car before coming to rest =Area of

= 25/6 m

= 4.16 m

∴ Clearly the first car will travel farther (36.11 m) than the first car(4.16 m).

Question 26. Fig 8.11 shows the distance-time graph of three objects A, B and C. Study the graph and answer the following Questions :

(a) Which of the three is travelling the fastest?

(b) Are all three ever at the same point on the road?

(c) How far has C travelled when B passes A?

(d) How far has B travelled by the time it passes C?

Solution :

(a) It is clear from graph that B covers more distance in less time. Therefore, B is the fastest.

(b) All of them never come at the same point at the same time.

(c) According to graph; each small division shows about 0.57 km.

A is passing B at point S which is in line with point P (on the distance axis) and shows about 9.14 km

Thus, at this point C travels about

9.14 – (0.57 x 3.75)km

= 9.14 km – 2.1375 km

= 7.0025 km

Thus, when A passes B, C travels about 7 km.

(d) B passes C at point Q at the distance axis which is

=5.28 km

Therefore, B travelled about 5.28 km when passes to C.

Question 27. A ball is gently dropped from a height of 20 m. If its velocity increases uniformly at the rate of 10m s-2 , with what velocity will it strike the ground? After what time will it strike the ground?
Solution :

Let us assume, the final velocity with which ball will strike the ground be ‘v’ and time it takes to strike the ground be ‘t’

Initial Velocity of ball u=0

Distance or height of fall s=20m

Downward acceleration a

As we know,

Or, 2as =

∴ Final velocity of ball, v

t= (v-u)/a

∴ Time taken by the ball to strike= (20-0)/10

= 20/10

= 2 seconds

Question 28. The speed-time graph for a car is shown is Fig. 8.12.

Fig. 8.12

(a) Find how far does the car travel in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during the period.

(b) Which part of the graph represents uniform motion of the car?

Solution :

(a) Distance travelled by car in the 4 second

The area under the slope of the speed – time graph gives the distance travelled by an object.

In the given graph

56 full squares and 12 half squares come under the area slope for the time of 4 second.

Total number of squares = 56 + 12/2 = 62 squares

The total area of the squares will give the distance travelled by the car in 4 second. on the time axis,

5 squares = 2seconds, therefore 1 square = 2/5 seconds

on speed axis there are 3 squares = 2m/s

therefore, area of one square

= = 4/15 m

so area of 62 squares=

= 248/15 m = 16.53 m

Hence the car travels 16.53m in the first 4 seconds.

(b) The straight line part of graph, from point A to point B represents a uniform motion of car.

Question 29. State which of the following situations are possible and give an example for each of these:

(a) an object with a constant acceleration but with zero velocity

(b) an object moving in a certain direction with an acceleration in the perpendicular direction.

Solution :

(a) An object with a constant acceleration can still have the zero velocity. For example an object which is at rest on the surface of earth will have zero velocity but still being acted upon by the gravitational force of earth with an acceleration of 9.81 ms-2 towards the center of earth. Hence when an object starts falling freely can have contant acceleration but with zero velocity.

(b) When an athlete moves with a velocity of constant magnitude along the circular path, the only change in his velocity is due to the change in the direction of motion. Here, the motion of the athlete moving along a circular path is, therefore, an example of an accelerated motion where acceleration is always perpendicular to direction of motion of an object at a given instance. Hence it is possible when an object moves on a circular path.

Question 30. An artificial satellite is moving in a circular orbit of radius 42250 km. Calculate its speed if it takes 24 hours to revolve around the Earth. \textbf

{Solution:} \begin{itemize} \item \textbf{Radius of the orbit:} \[ r = 42250 \, \text{km} = 42250 \times 1000 \, \text{m} = 42250000 \, \text{m} \] \item \textbf{Time taken for one revolution:} \[ T = 24 \, \text{hours} = 24 \times 60 \times 60 \, \text{seconds} = 86400 \, \text{seconds} \] \item \textbf{Speed of the satellite:} The speed \( v \) is given by the formula: \[ v = \frac{\text{Distance}}{\text{Time}} \] The distance traveled in one complete revolution is the circumference of the orbit: \[ \text{Distance} = 2 \pi r \] Substituting the values: \[ \text{Distance} = 2 \times 3.14 \times 42250000 \, \text{m} \approx 265600000 \, \text{m} \] Therefore, the speed \( v \) is: \[ v = \frac{265600000 \, \text{m}}{86400 \, \text{s}} \approx 3073.74 \, \text{m/s} \] Converting the speed to kilometers per second: \[ v \approx 3.07 \, \text{km/s} \] \end{itemize} Thus, the speed of the satellite is approximately \( 3073.74 \, \text{m/s} \) or \( 3.07 \, \text{km/s} \).